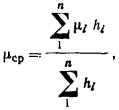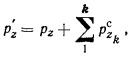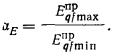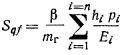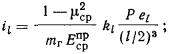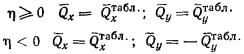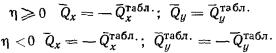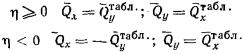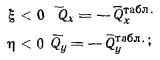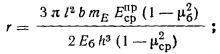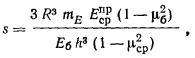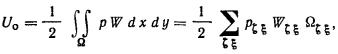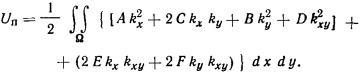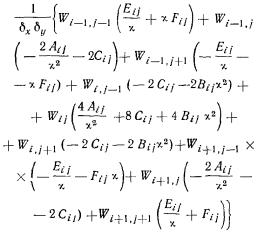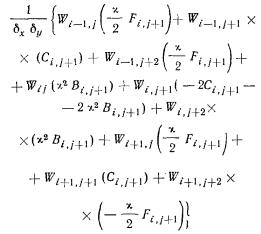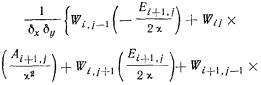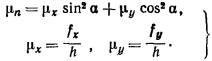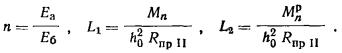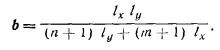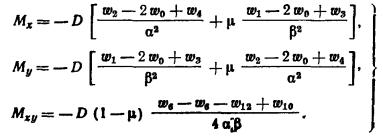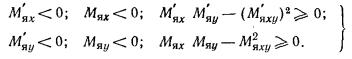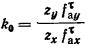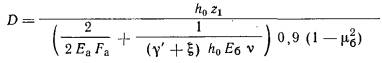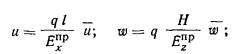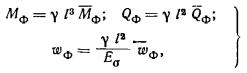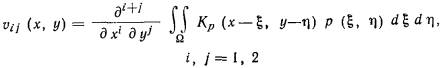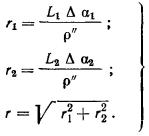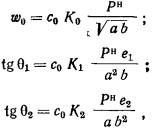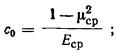| |
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ
ОСНОВАНИЙ И ПОДЗЕМНЫХ СООРУЖЕНИЙ ИМ. Н.М. ГЕРСЕВАНОВА
(НИИОСП ИМ. Н.М. ГЕРСЕВАНОВА)
ГОССТРОЯ СССР
Руководство
по проектированию плитных фундаментов
каркасных зданий и сооружений башенного типа
|

|
Москва
СТРОЙИЗДАТ
1984
|
Разработано к СНиП II-15-74.
Даны рекомендации по проектированию
произвольной ортогональной, полигональной и круглой формы в плане
железобетонных плитных фундаментов каркасных зданий и сооружений башенного типа
на естественном основании, по выбору расчетных схем и параметров основания, в
том числе переменного коэффициента жесткости, основания, расчету деформаций
основания с расчетной схемой в виде линейно-деформируемого слоя, по определению
предварительных размеров плитных фундаментов. Приведены особенности конструирования
и наблюдений за осадками, сдвигами и кренами плитных фундаментов.
Для инженерно-технических работников
проектных организаций.
Содержание
Сплошные монолитные железобетонные
плитные фундаменты прямоугольной, произвольной ортогональной либо полигональной
и круглой формы в плане широко используются при строительстве на естественном
основании (особенно на слабых и неоднородных грунтах) многоэтажных зданий различного
назначения, а также промышленных сооружений типа силосов, элеваторов, дымовых
труб и т.п. Площадь таких плит, как правило, превышает 100 м2, а
ширина или диаметр b(d) ≥ 10 м.
За последние годы в нашей стране
проведены большие теоретические и экспериментальные исследования плитных
фундаментов, завершившиеся разработкой методов и созданием программ для расчета
плитных фундаментов на ЭВМ.
Методы и программы для расчета плитных
фундаментов разработаны на основе последних достижений в области строительной
механики, теории расчета железобетонных конструкций, механики грунтов, теории
упругости, вычислительной математики и практики фундаментостроения. Они
позволяют рассчитывать плитные фундаменты практически любой формы в плане
(прямоугольные, круглые, кольцевые, сложной формы) переменной толщины с учетом
влияния жесткости верхнего строения в виде каркаса, системы связанных между
собой жестких диафрагм, несущих стен или очень жесткого надфундаментного
строения типа силосных корпусов, дымовых труб и т.п. Стал возможным совместный
расчет в упругой постановке элементов связевого или рамного каркаса и плитного
фундамента, а также расчет плитного фундамента с учетом особенностей
деформирования железобетона.
В связи с этим «Руководство по
проектированию фундаментных плит каркасных зданий» (1977 г.) полностью
переработано и дополнено.
В Руководстве даются рекомендации и
примеры по выбору расчетных схем и параметров основания, в том числе
переменного коэффициента жесткости основания, по расчету деформаций основания с
расчетной схемой в виде линейно-деформируемого слоя, по определению
предварительных размеров плитного фундамента по условию минимального объема
бетона, по выбору методов и программ на ЭВМ для расчета плитных фундаментов
произвольной ортогональной, полигональной и круглой формы в плане зданий и
сооружений, а также круглых и кольцевых фундаментов с коническими оболочками
для сооружений башенного типа. Обращено внимание на особенности конструирования
плитных фундаментов. Изложены требования к измерениям осадок, сдвигов и кренов
плитных фундаментов.
В приложениях к Руководству даны основные
характеристики программ для ЭВМ, позволяющих подобрать минимальные
предварительные размеры плитных фундаментов, а затем выполнить расчет
фундаментов переменной жесткости с учетом особенностей деформирования
железобетона, трения на поверхности контакта фундамента с грунтом, влияния
жесткости надфундаментного строения в виде каркаса и стен здания, очень
жесткого ствола дымовой трубы, банок силосных корпусов и других, а также произвести
совместный расчет различных схем каркаса здания и плитного фундамента. Кроме
того, приведены графики для быстрого определения осадок и кренов прямоугольных
и круглых жестких фундаментов на основании в виде линейно-деформируемого
полупространства и слоя конечной толщины.
Руководство составили: разд. 1
«Основные положения» - канд. техн. наук Т.А. Маликова (НИИОСП); разд. 2
«Расчет основания по деформациям» - д-р. техн. наук, проф. К.Е. Егоров, канд.
техн. наук Т.А. Маликова (НИИОСП); разд.
3 «Определение предварительных размеров плитного фундамента по условию
минимального объема бетона» - канд. техн. наук Т.А. Маликова (табл. 11 - инж. С.А. Компанейский, Моспроект-2); разд.
4 «Определение коэффициентов жесткости основания плитного фундамента» -
канд. техн. наук Т.А. Маликова; разд. 5 «Статические
расчеты плитных фундаментов», подраздел «Расчет плитного фундамента с учетом
влияния стен здания» - д-р техн. наук, проф. В.И. Соломин; инж. А.С. Сытник
(Челябинский политехнический институт - ЧПИ); подраздел «Расчет плитного
фундамента здания с учетом особенностей деформирования железобетона» - д-р
техн. наук, проф. В.И. Соломин, канд. техн. наук В.Л. Высоковский (ЧПИ);
подраздел «Совместный расчет плитного фундамента и рамного каркаса здания» -
канд. техн. наук Е.Б. Фрайфельд (Харьковский Промстройниипроект); подраздел
«Совместный расчет плитного фундамента и надфундаментного строения здания со
связевым или рамно-связевым каркасом, а также панельного и кирпичного дома» -
канд. техн. наук М.С. Вайнштейн (Моспроект-1); подраздел «Расчет плитных
фундаментов с учетом влияния рамного каркаса здания» - канд. техн. наук В.И.
Обозов (ЦНИИСК); подразделы «Расчет прямоугольных плитных фундаментов зданий с
рамным каркасом при учете жесткости каркаса и реактивных касательных
напряжений», «Расчет прямоугольных плитных фундаментов зданий со связевым
каркасом при учете реактивных касательных напряжений» и «Расчет толстых плитных
фундаментов с учетом реактивных касательных напряжений» - д-р техн. наук, проф.
И.И. Гудушаури, канд. техн. наук В.И. Ломидзе, инж. А.Д. Джакели (Грузинский
НИИ энергетики и гидротехнических сооружений); подраздел «Расчет сплошных
железобетонных плитных фундаментов под сетку колонн по кинематическому методу
предельного равновесия» - д-р техн. наук, проф. Ю.Н. Мурзенко (Новочеркасский
политехнический институт), канд. техн. наук А.А. Цессарский (Киевское отделение
ВНИИГС), инж. С.И. Политов (НПИ); подраздел «Расчет плитных фундаментов с
учетом жесткости силосных корпусов» - канд. физ.-мат. наук В.И. Сливкер, канд.
техн. наук К.П. Галасова (Ленпромстройпроект); подразделы «Совместный расчет
плитных фундаментов элеваторов и надфундаментных конструкций конечной
жесткости» и «Расчет прямоугольного плитного фундамента, взаимодействующего с
деформируемым основанием и жестким надфундаментным строением» - кандидаты техн.
наук Е.З. Болтянский, Ю.Ю. Чинилин (ЦНИИПромзернопроект); подраздел «Расчет
круглых и кольцевых плитных фундаментов с коническими оболочками для сооружений
башенного типа» - д-р техн. наук, проф. В.И. Климанов, инж. А.Г. Литвиненко,
В.П. Каваева, А.И. Макаров (Уральский Промстройниипроект); подраздел «Расчет
круглых и кольцевых плитных фундаментов сооружений башенного типа с учетом
особенностей деформирования железобетона» - д-р техн. наук, проф. В.И. Соломин,
канд. техн. наук С.Б. Шматков (ЧПИ); подраздел «Расчет круглых плитных
фундаментов с учетом особенностей деформирования основания с переменными
физико-механическими характеристиками» - д-р физ.-матем. наук, проф. В.М.
Александров, канд. физ.-матем. наук Г.Н. Павлик (РГУ); разд.
6 «Конструктивные требования» - инж. И.Я. Дрибинский, Ю.Д. Коломийченко,
канд. техн. наук В.С. Урисман (Харьковский Промстройниипроект); разд.
7 «Требования к измерениям осадок, сдвигов и кренов плитных фундаментов»,
подраздел «Измерение осадок» - канд. техн. наук Т.А. Маликова, подразделы
«Измерение сдвигов» и «Измерение кренов» - канд. техн. наук О.В. Китайкина
(НИИОСП); прил.
1 - канд. техн. наук Т.А. Маликова (НИИОСП) прил. 2 и 3
- канд. техн. наук В.С. Урисман (Харьковский Промстройниипроект).
табл.
12 - 21, 24 - 42, 49 - 58
заимствованы из книги д-ра техн. наук, проф. М.И. Горбунова-Посадова «Таблицы
для расчета тонких плит на упругом основании» (М., Госстройиздат, 1958).
Руководство разработано под общей
редакцией д-ра техн. наук, проф. К.Е. Егорова и канд. техн. наук Т.А.
Маликовой.
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
1.1. Настоящее
Руководство рекомендуется использовать при проектировании крупноразмерных
(шириной b ≥ 10 м или диаметром d ≥ 10
м) прямоугольных, произвольной ортогональной, полигональной, круглой формы в
плане железобетонных плитных фундаментов каркасных зданий и сооружений
башенного типа (силосных корпусов, дымовых труб, теле- и радиобашен и т.п.) на
естественном основании, не подверженном сейсмическим воздействиям и не
находящемся в районе особых грунтовых условий (просадочных, набухающих,
засоленных грунтов, подрабатываемых и закарстованных территорий).
Руководством допускается пользоваться при
проектировании зданий и сооружений других систем (бескаркасных, со смешанным
каркасом и др.).
1.2. Плитные фундаменты и их основания следует
проектировать в соответствии с требованиями глав СНиП на нагрузки и
воздействия, по проектированию бетонных и железобетонных конструкций, а также
оснований зданий и сооружений с учетом указаний инструкций на проектирование
сооружений башенного типа (элеваторов, силосных складов сыпучих материалов,
дымовых труб, доменных печей и др.), нормативных документов, содержащих
требования к материалам и правилам производства работ, а также в соответствии с
настоящим Руководством.
1.3. Расчет плитных фундаментов зданий, строящихся в
особых грунтовых условиях, допускается выполнять по рекомендациям настоящего
Руководства, при этом необходимо дополнительно пользоваться следующими
нормативными документами для подготовки исходных данных к расчету:
«Руководством по расчету и проектированию зданий и сооружений на
подрабатываемых территориях» (М., 1977), «Инструкцией по проектированию
бескаркасных жилых домов, строящихся на просадочных грунтах с применением
конструктивных мероприятий» (РСН 297-78), а также главой СНиП на проектирование
зданий и сооружений на подрабатываемых территориях.
1.4. Проектирование плитных фундаментов необходимо
осуществлять на основе:
результатов инженерно-геологических
изысканий места строительства;
опыта возведения и эксплуатации
сооружений с плитными фундаментами в аналогичных инженерно-геологических
условиях строительства;
технического задания на проектирование
здания или сооружения, условий производства работ и последующей эксплуатации;
технико-экономического сравнения
возможных вариантов проектного решения.
1.5. Конструкция железобетонного плитного фундамента
должна обеспечивать прочность и надежность здания или сооружения и выбираться в
зависимости от конструктивной схемы сооружения, величины и характера
воздействий, несущей способности и деформативности основания при минимальном
расходе материалов и трудоемкости.
1.6. Для плитного фундамента должен применяться бетон
марки не ниже М 200.
1.7. Под плитные
фундаменты следует устраивать бетонную подготовку из бетона марки не ниже М 50,
толщину которой определяют в зависимости от условий, методов производства работ
и принимают не менее 100 мм. При водонасыщенном глинистом основании бетон
подготовки рекомендуется укладывать на песчаную подушку толщиной не менее 200
мм.
1.8. В случае агрессивных грунтовых вод следует
предусматривать антикоррозионные мероприятия по защите плитного фундамента в
соответствии с указаниями главы СНиП на защиту строительных конструкций от
коррозии.
1.9. При производстве земляных работ необходимо
предусмотреть мероприятия по сохранению природной структуры грунтов основания,
принимая в необходимых случаях зачистку дна котлована вручную
1.10. Натурные измерения деформаций оснований и плитных
фундаментов в процессе строительства и эксплуатации здания или сооружения
должны предусматриваться в соответствии с указаниями пп. 17 и 3.71 главы СНиП
на проектирование оснований зданий и сооружений. Для этого при разработке
рабочих чертежей нулевого цикла нужно составить проект изготовления и закладки
плитных, глубинных марок и глубинных реперов (см. разд.
7), включить стоимость этих работ в смету на строительство здания или
сооружения, а также предусмотреть средства на проведение геодезических
измерений.
1.11. Предварительную оценку инженерно-геологических
условий площадки строительства и выбор типа фундаментов выполняют на основе
предварительных изысканий.
1.12. Техническое задание на проведение
инженерно-геологических изысканий при предварительно выбранном типе фундамента
в виде сплошной плиты составляет проектный институт в соответствии с указаниями
главы СНиП на проектирование оснований зданий и сооружений, главы СНиП на
выполнение инженерных изысканий для строительства, а также документов,
развивающих эту главу СНиП.
1.13. Программу инженерно-геологических изысканий
подготавливает изыскательская организация согласно техническому заданию
проектного института и в соответствии с требованиями главы СНиП на выполнение
инженерных изысканий и согласовывает с этим институтом.
1.14. Техническим заданием на проведение
инженерно-геологических изысканий на территории строительства должна быть
предусмотрена проходка следующих скважин:
разведочных на глубину 40 - 50 м с
расстоянием между ними не более 50 м и не менее одной на сооружение;
инженерно-геологических, число которых
должно быть не менее пяти: по углам и в центре плиты; допускается размещение
скважин между двумя соседними сооружениями, если расстояние между ними не
превышает 10 м.
Число разведочных и
инженерно-геологических скважин и расстояния между ними определяют в
зависимости от изученности и сложности геологических условий площадки
строительства, а также с учетом размеров и назначения здания или сооружения.
1.15. Глубину проходки инженерно-геологических скважин
принимают равной:
расстоянию от дневной поверхности до слоя
скального грунта, обнаруженного на глубине, меньшей 20 м от проектируемой
подошвы фундаментной плиты;
половине ширины фундамента, но не менее
20 м, если скальные грунты залегают на большей глубине.
Если на глубине, большей половины ширины
фундамента и большей 20 м, обнаружен слой слабого грунта, необходимо скважину
углубить, пройдя слой этого грунта.
Для элеваторных сооружений и силосных
складов требуется корректировка указанных глубин бурения в соответствии с
расчетной глубиной сжимаемой толщи основания.
1.16. Техническое задание на проведение
инженерно-геологических изысканий на территории строительства дымовой трубы
следует составлять с учетом требований «Рекомендаций по производству
инженерно-геологических изысканий для дымовых труб» (НИИОСП. М.: Стройиздат,
1980).
1.17. В техническое задание на изыскания необходимо
включать проведение статического и динамического зондирования* для
выявления неоднородности грунтов, их прочностных и деформационных
характеристик.
* ГОСТ 20069-74
«Грунты. Метод полевого испытания статическим зондированием» и «Указания
по зондированию грунтов для строительства» СН 448-72.
1.18. Модули деформации нескальных грунтов основания
следует, как правило, определять в полевых условиях при проходке
инженерно-геологических скважин, а также в шурфах и шахтах загружением штампа
статическими нагрузками* в соответствии с требованиями главы СНиП на
проектирование оснований зданий и сооружений.
*ГОСТ
12374-77 «Грунты. Метод полевого испытания статическими нагрузками».
1.19. Методы определения деформационных и прочностных
характеристик грунтов основания необходимо выбирать в соответствии с указаниями
пп. 3.25 - 3.35 «Руководства
по проектированию оснований зданий и сооружений» (НИИОСП. М.: Стройиздат,
1977).
1.20. Гидростатические исследования должны включать
определение расчетного уровня основного горизонта грунтовых вод,
прогнозирование верховодки на время производства работ и эксплуатации здания
или сооружения, изменения химического состава грунтовых вод в период эксплуатации
здания или сооружения, а также установление степени агрессивности грунтовых
вод.
1.21. Плитный фундамент должен удовлетворять требованиям
расчета по несущей способности (предельные состояния первой группы) и по
пригодности к нормальной эксплуатации (предельные состояния второй группы),
принимаемым в соответствии с указаниями главы СНиП на проектирование бетонных и
железобетонных конструкций.
1.22. Величины нагрузок и воздействий на плитный фундамент,
значения коэффициентов перегрузок, коэффициентов сочетаний, а также
подразделение нагрузок на постоянные и временные, длительные, кратковременные,
особые следует принимать в соответствии с требованиями главы СНиП по нагрузкам
и воздействиям.
1.23. При определении площадок загружения фундамента
следует нагрузку, передаваемую подколонниками (банкетками) или стенами,
приводить к срединной поверхности фундамента, распределяя ее под углом 45° от
нижнего обреза подколонников или стен.
Собственный вес плитного фундамента
допускается не учитывать в случае песчаного основания, принимать с
коэффициентом 0,5 при глинистом основании и учитывать плотностью, если плитный
фундамент лежит на основании, сложенном слабыми грунтами с модулем деформации Е < 5 МПа.
1.24. Основание плитного фундамента также должно
рассчитываться по двум группам предельных состояний:
по первой группе - по несущей
способности;
по второй группе - по деформациям
(осадкам, прогибам и пр.), создающим препятствия для нормальной эксплуатации
зданий и сооружений.
1.25. Основание плитного фундамента рассчитывают по несущей
способности, если фундамент расположен на бровке откоса, вблизи крутопадающего
слоя грунта, или если оно сложено скальными грунтами.
1.26. Усилия в плитном фундаменте и его деформации, а также
деформации основания рекомендуется определять расчетом из условия совместной
работы надфундаментной конструкции, фундамента и основания с учетом
неоднородности основания по глубине и в плане, распределяющей способности
основания, воздействия соседних зданий и сооружений, а также неупругих
деформаций грунта, бетона и арматуры фундамента, материала элементов
надфундаментных конструкций и наличия трещин в фундаменте.
1.27. Для упрощения расчета плитного фундамента допускается
не учитывать влияние на распределение усилий в фундаменте заглубления
фундамента и реактивных касательных напряжений по подошве. Допускается также
использовать приближенные приемы учета неупругих деформаций основания,
фундамента и элементов надфундаментных конструкций либо выполнять расчет
плитного фундамента в предположении линейно-упругого деформирования материала
фундамента, элементов надфундаментных конструкций и грунтов основания (в так
называемой линейной постановке задачи) с использованием принципа независимости
действия сил, а подбор арматуры и проверку прочности сечений фундамента
производить на найденные усилия в соответствии с указаниями главы СНиП на
проектирование бетонных и железобетонных конструкций.
1.28. Расчет системы надфундаментные конструкции -
фундамент - основание рекомендуется выполнять с учетом последовательности
возведения сооружения.
1.29. При расчете плитного фундамента допускается применять
как непрерывные (континуальные) расчетные схемы, так и дискретные.
1.30. Для упрощения совместного расчета системы основание -
фундамент - надфундаментные конструкции допускается выполнять раздельный расчет
основания, плитного фундамента на сжимаемом основании и надфундаментных
конструкций. Результаты расчета основания используют для определения
предварительных минимальных размеров плитного фундамента и параметров
основания, необходимых для статического расчета фундамента на сжимаемом
основании.
Раздельный расчет фундамента на сжимаемом
основании и надфундаментных конструкций в необходимых случаях может быть
выполнен с использованием метода последовательных приближений.
1.31. Расчет плитных фундаментов следует выполнять на ЭВМ
по программам, прошедшим апробацию. Такие программы и инструкции к ним
публикуются в фонде алгоритмов и программ ЦНИИпроекта.
Основные характеристики программ для
расчета плитных фундаментов на ЭВМ приведены в прил.
1 (по состоянию на 01.10.1983).
1.32. При расчете деформаций
основания нагрузки на него допускается определять без учета их
перераспределения надфундаментной конструкцией и принимать в соответствии со
статической схемой здания или сооружения.
1.33. Расчет деформаций основания производят на основное сочетание расчетных нагрузок,
взятых с коэффициентом перегрузки, равным
1.
Расчет основания по несущей способности
выполняют на основное сочетание расчетных нагрузок с коэффициентом перегрузки,
принимаемым по указаниям главы СНиП на нагрузки и воздействия, при наличии
особых нагрузок и воздействий - на основное и особое сочетания нагрузок.
Во всех расчетах оснований фундаментов
кратковременные нагрузки должны приниматься с коэффициентами сочетаний, а
временные нагрузки на перекрытия многоэтажных зданий - с понижающими
коэффициентами, учитывающими вероятность одновременного загружения перекрытий,
в соответствии с требованиями главы СНиП на нагрузки и воздействия и инструкций
на проектирование фундаментов сооружений башенного типа (элеваторов, дымовых
труб и др.).
1.34. Расчет деформаций основания без учета совместной работы с фундаментом
допускается выполнять, применяя расчетную схему основания в виде:
линейно-деформируемого полупространства с
условным ограничением глубины z' сжимаемой толщи;
линейно-деформируемого слоя.
Расчетную схему для расчета основания по
деформациям устанавливают по рекомендациям разд. 2 настоящего Руководства.
Расчет деформаций основания с
использованием указанных расчетных схем следует выполнять в соответствии с
требованиями прил. 3 главы СНиП на проектирование оснований зданий и
сооружений, а также по рекомендациям разд. 2 настоящего Руководства.
1.35. В расчете плитного фундамента на сжимаемом основании
допускается не учитывать пластические деформации грунтов основания, если при
расчете основания учтены требования главы СНиП на проектирование оснований
зданий и сооружений в части условного ограничения развития зон пластических
деформаций грунта под краями фундамента.
В этом случае для расчета плитного
фундамента на однородном по сжимаемости в плане основании (αE ≤ 1,5, см. п.
2.23) принимают расчетную схему в виде линейно-деформируемого слоя со
следующими параметрами: толщиной слоя H, приведенным в пределах этого слоя и осредненным в
пределах плана плиты модулем деформации 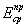 , осредненным
в пределах слоя коэффициентом Пуассона μср. , осредненным
в пределах слоя коэффициентом Пуассона μср.
Для упрощения расчета плитного фундамента
на однородном основании допускается использовать расчетные схемы в виде:
линейно-деформируемого однородного полупространства при условии введения в
расчет приведенного осредненного модуля деформации основания  с корректирующим
коэффициентом-множителем mE и осредненного коэффициента Пуассона μср; основания,
характеризуемого переменным коэффициентом жесткости, который приближенно
учитывает распределительную способность основания. с корректирующим
коэффициентом-множителем mE и осредненного коэффициента Пуассона μср; основания,
характеризуемого переменным коэффициентом жесткости, который приближенно
учитывает распределительную способность основания.
В случае неоднородного в плане основания
(αЕ > 1,5) при
расчете плитного фундамента принимают расчетную схему основания,
характеризуемого переменным коэффициентом жесткости, который приближенно
учитывает неоднородность основания в плане и по глубине, а также
распределительную способность основания.
1.36. Параметры линейно-деформируемого слоя и однородного
линейно-деформируемого полупространства следует находить по указаниям разд. 2
Руководства.
Сближение результатов расчета плитного
фундамента на линейно-деформируемом полупространстве и слое осуществляют по
условию равенства средних осадок, вводя в расчет фундамента на основании в виде
линейно-деформируемого полупространства корректирующий коэффициент - множитель mЕ при модуле
деформации основания 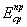 , определяемый по п. 3.11
настоящего Руководства. , определяемый по п. 3.11
настоящего Руководства.
Величины переменного коэффициента
жесткости основания находят по указаниям разд.
4.
1.37. Предельно допустимые величины совместных деформаций
основания и здания или сооружения определяют по указаниям главы СНиП на
проектирование оснований зданий и сооружений.
1.38. Подбор сечений плитного фундамента производят в
соответствии с требованиями главы СНиП на проектирование бетонных и
железобетонных конструкций по прочности и по раскрытию трещин. К
трещиностойкости железобетона плитного фундамента при отсутствии специальных
обоснований предъявляются требования III
категории, в соответствии с которыми допускается ограниченное по ширине
кратковременное и длительное раскрытие нормальных и наклонных трещин.
2. РАСЧЕТ ОСНОВАНИЯ ПО
ДЕФОРМАЦИЯМ
2.1. В настоящем разделе изложен расчет основания по
деформациям с использованием расчетной схемы в виде линейно-деформируемого слоя
(см. п.
1.34).
При расчете деформаций основания с
использованием расчетной схемы основания в виде линейно-деформируемого
полупространства (см. разд. 1) следует руководствоваться указаниями
главы СНиП по проектированию оснований зданий и сооружений.
2.2. Расчет основания по
деформациям производят для определения минимальных размеров плитного
фундамента, при которых выполняются
конструктивные ограничения и требования главы СНиП на проектирование оснований
зданий и сооружений, предъявляемые к давлению под подошвой фундамента и на
кровлю грунта, находящегося в пределах сжимаемой толщи основания и имеющего
сжимаемость, меньшую сжимаемости вышележащих слоев, а также к осадкам и кренам
фундамента.
2.3. Подбор минимальных
размеров фундамента производят шаговым методом, путем изменения длины
консольных участков плитного фундамента и проверок (на каждом шаге) выполнения
требований, предъявляемых главой СНиП на проектирование оснований зданий и
сооружений к величинам, перечисленным в п. 2.2. Шаг увеличения длины консольных
участков фундамента следует принимать равным 300 мм. Учитывая трудоемкость
вычислений, рекомендуется выполнять эти расчеты на ЭВМ с помощью программного
комплекса «GEST-82», основные характеристики
которого приведены в прил.
1.
2.4. При учете различной сжимаемости слоев грунта,
находящихся в пределах сжимаемой толщи основания, толщину каждого слоя грунта
допускается принимать:
осредненной в пределах плана плиты при
определении глубины сжимаемой толщи основания (при расчетной схеме основания в
виде линейно-деформируемого полупространства) и толщины Н сжимаемого слоя основания (при
расчетной схеме основания в виде линейно-деформируемого слоя), при выборе
расчетной схемы основания, вычислении средней осадки основания и крена
фундамента от внецентренного действия нагрузки;
по вертикали, проходящей через
рассматриваемую точку фундамента, при вычислении осадок центра, угловых точек,
середин сторон и других точек фундамента.
2.5. Для выбора расчетной схемы основания следует
предварительно определить глубину z' сжимаемой
толщи основания по указаниям прил. 3 главы СНиП на проектирование оснований
зданий и сооружений и толщину Н
сжимаемого слоя основания в соответствии с рекомендациями настоящего
Руководства.
2.6. Расчетную толщину
линейно-деформируемого слоя Н основания,
сложенного глинистыми или песчаными грунтами, определяют по формуле
где
b - ширина фундамента, м;
Нo и t - величины,
принимаемые соответственно равными для оснований, сложенных глинистыми
грунтами, - 9 м и 0,15, песчаными - 6 м
и 0,1;
kp - коэффициент, учитывающий фактическое давление на основание, принимаемый равным 0,8 при давлении р = 0,1 МПа и 1,4 при давлении р = 0,6 МПа (при промежуточных давлениях
значение kp определяют линейной интерполяцией).
Для элеваторных сооружений и силосных складов значение
коэффициента t следует принимать равным 0,75
для оснований, сложенных глинистыми грунтами, и 0,5 - песчаными.
Для фундаментов дымовых труб диаметром
более 80 м коэффициент t следует
принимать равным 0,3 для оснований, сложенных глинистыми грунтами, и 0,2 -
песчаными.
2.7. Значение Н для основания, сложенного глинистыми и
песчаными грунтами, определяют как средневзвешенное. Для этого сначала
вычисляют значение Н в предположении,
что основание сложено только песчаными Нп
или только глинистыми Нг
грунтами.
При наличии в основании до глубины Нп (от подошвы фундамента) слоев глинистого грунта различают
следующие случаи (рис. 1).
1) в пределах от Нп до Нг
залегают только песчаные грунты
где
 - суммарная толщина глинистых слоев до
глубины Нп; - суммарная толщина глинистых слоев до
глубины Нп;
2) в пределах от Нп до Нг залегают только глинистые грунты
3) в пределах Нп до Нг залегают и песчаные и глинистые грунты
|
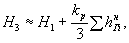
|
(4)
|
где
 - суммарная толщина глинистых слоев в
пределах глубины от Нп до Н1. - суммарная толщина глинистых слоев в
пределах глубины от Нп до Н1.
Допускается в этом случае принимать
|
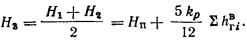
|
(5)
|
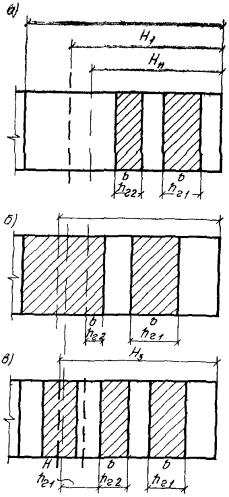
Рис. 1. Взаимное расположение слоев
глинистого и песчаного грунта в пределах сжимаемой толщи основания
а - в пределах от Нп до Нг
залегают только песчаные грунты, б -
то же, только глинистые грунты, в -
то же, глинистые и песчаные грунты
2.8. Толщину Нэ линейно-деформируемого слоя, эквивалентного по средней осадке
линейно-деформируемому полупространству с глубиной сжимаемой толщи z', следует определять по
зависимости
|
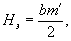
|
(6)
|
где
m' - величина, определяемая по табл. 1 в зависимости от
отношения длины к ширине прямоугольного плитного фундамента n = l/b и отношения глубины сжимаемой толщи
линейно-деформируемого полупространства к полуширине фундамента m = 2z'/b.
Таблица 1
|
m = 2z'/b
|
Коэффициент
m' = 2H/b
при отношении сторон прямоугольной загруженной площади n = l/b
|
|
1
|
1,5
|
2
|
3
|
4
|
∞
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0,2
|
0,13
|
0,13
|
0,13
|
0,13
|
0,13
|
0,13
|
|
0,4
|
0,27
|
0,27
|
0,27
|
0,27
|
0,27
|
0,27
|
|
0,6
|
0,41
|
0,41
|
0,41
|
0,41
|
0,41
|
0,41
|
|
0,8
|
0,56
|
0,56
|
0,56
|
0,56
|
0,56
|
0,56
|
|
1
|
0,71
|
0,71
|
0,71
|
0,71
|
0,71
|
0,71
|
|
1,2
|
0,86
|
0,86
|
0,86
|
0,86
|
0,86
|
0,86
|
|
1,4
|
1,01
|
1,02
|
1,02
|
1,02
|
1,02
|
1,03
|
|
1,6
|
1,16
|
1,19
|
1,19
|
1,19
|
1,19
|
1,21
|
|
1,8
|
1,31
|
1,35
|
1,36
|
1,36
|
1,36
|
1,37
|
|
2
|
1,44
|
1,51
|
1,53
|
1,53
|
1,53
|
1,56
|
|
2,2
|
1,59
|
1,67
|
1,70
|
1,70
|
1,70
|
1,75
|
|
2,4
|
1,76
|
1,83
|
1,88
|
1,88
|
1,88
|
1,93
|
|
2,6
|
1,92
|
2,00
|
2,05
|
2,08
|
2,08
|
2,11
|
|
2,8
|
2,07
|
2,17
|
2,23
|
2,27
|
2,27
|
2,30
|
|
3
|
2,23
|
2,32
|
2,41
|
2,45
|
2,45
|
2,48
|
|
3,2
|
2,37
|
2,48
|
2,58
|
2,64
|
2,64
|
2,67
|
|
3,4
|
2,54
|
2,66
|
2,75
|
2,84
|
2,85
|
2,88
|
|
3,6
|
2,71
|
2,85
|
2,96
|
3,05
|
3,09
|
3,11
|
|
3,8
|
2,90
|
3,06
|
3,18
|
3,27
|
3,31
|
3,33
|
|
4
|
3,12
|
3,29
|
3,40
|
3,49
|
3,54
|
3,56
|
|
4,2
|
3,35
|
3,54
|
3,65
|
3,72
|
3,78
|
3,80
|
|
4,4
|
3,60
|
3,79
|
3,89
|
3,96
|
4,01
|
4,04
|
|
4,6
|
3,86
|
4,04
|
4,15
|
4,23
|
4,29
|
4,29
|
|
4,8
|
4,14
|
4,30
|
4,43
|
4,51
|
4,56
|
4,56
|
|
5
|
4,43
|
4,60
|
4,73
|
4,82
|
4,87
|
4,87
|
|
5,2
|
4,75
|
4,96
|
5,14
|
5,23
|
5,29
|
5,29
|
|
5,4
|
5,14
|
5,49
|
5,74
|
5,90
|
5,86
|
5,86
|
2.9. Расчет деформаций основания следует выполнять,
применяя расчетную схему основания в виде линейно-деформируемого
полупространства с условным ограничением глубины z' сжимаемой толщи, если:
а) модули деформации грунтов E < 10
МПа всех слоев, расположенных в пределах сжимаемой толщи z', или модули деформации грунтов E < 10
МПа всех слоев, кроме одного с модулем деформации E1 ≥
100 МПа, подстилаемого слоем грунта с модулем деформации Е2 < Е1 и не выполняется условие
|
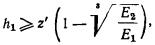
|
(7)
|
где
h1 - толщина слоя грунта с модулем деформации E1;
б) суммарная толщина слоев
грунта с модулем деформации E < 10 МПа, залегающих ниже подошвы фундамента до
глубины H, больше 0,2 Н;
в) суммарная толщина слоев
грунта с модулем деформации E < 10 МПа, залегающих ниже подошвы фундамента до
глубины H, не превышает 0,2 Н,
а с глубины H до z' - больше 0,2 Н и расстояние z' от подошвы фундамента до последнего слоя грунта с
модулем деформации E < 10 МПа связано с величиной Hэ, определяемой по п.
2.8, неравенством z' ≥ Hэ.
2.10. Расчет деформаций
основания следует выполнять, применяя расчетную схему в виде
линейно-деформируемого слоя толщиной H, определяемой по пп. 2.6 и 2.7, если:
а) в пределах глубины z' от подошвы фундамента обнаружен слой грунта с модулем
деформации E1 ≥
100 МПа, подстилаемый слоем грунта с модулем деформации Е2 < Е1 и соблюдается условие (7);
б) модули деформации всех
заданных слоев грунта E ≥ 10 МПа;
в) суммарная толщина слоев
грунта с модулем деформации E < 10 МПа, залегающих ниже подошвы фундамента как
до глубины H, так и от глубины H до z', не превышает 0,2 Н;
г) суммарная толщина слоев
грунта с модулем деформации E < 10 МПа, залегающих ниже подошвы фундамента до
глубины H, не превышает 0,2 H, а с глубин H до z' больше 0,2 H и
расстояние z от подошвы плиты до подошвы
последнего слоя грунта с модулем деформации E < 10 МПа связано с величиной Hэ, определяемой по п.
2.8, неравенством z < Hэ.
2.11. Расчетная толщина H линейно-деформируемого слоя принимается равной
расстоянию z от подошвы фундамента до кровли
грунта с модулем деформации E1 ≥
100 МПа, находящегося в пределах глубины z' и подстилаемого грунтом с модулем деформации Е2 < Е1 если соблюдается условие (7).
2.12. Расчетная толщина линейно-деформируемого слоя Н, найденная по п. 2.11, должна быть
уменьшена и принята по указаниям пп.
2.6 и 2.7,
если слой грунта с модулем деформации E ≥ 100 МПа находится ниже глубины Н, рекомендуемой пп.
2.6 и 2.7,
и для основания независимо от условия п. 2.10 а принята расчетная схема в виде
линейно-деформируемого слоя.
2.13. Расчетная толщина Н линейно-деформируемого слоя основания, вычисленная по пп.
2.6 и 2.7,
должна быть увеличена на толщину слоя грунта с модулем деформации E < 10 МПа, расположенного на глубине Н (подстилающего сжимаемый слой), если
толщина этого слоя не превышает 0,2 Н.
2.14. Расчетная толщина Н линейно-деформируемого слоя основания, вычисленная по пп.
2.6 и 2.7,
должна быть принята равной расстоянию от подошвы плиты до последнего (в
пределах глубины z')
слоя грунта с модулем деформации E < 10
МПа, если выполняется условие п. 2.10 г.
2.15. Дополнительную
осадку силосных корпусов за счет многократно повторной нагрузки от веса
загружаемого продукта определяют для сжимаемой толщи, ограниченной глубиной z'пн , до которой распространяется влияние повторных
нагрузок (рис. 2).

Рис.
2. Схема для расчета дополнительных осадок основания от повторных нагрузок
Глубину сжимаемой толщи
основания z'пн при
расчете по схеме линейно-деформируемого полупространства определяют, исходя из
соотношения величины давления от повторно прикладываемой нагрузки 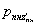 и полного давления,
равного сумме давлений от сооружения и полного давления,
равного сумме давлений от сооружения 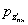 , и
природного , и
природного  на той же глубине. Для песчаных и глинистых грунтов
это соотношение следует принимать равным: на той же глубине. Для песчаных и глинистых грунтов
это соотношение следует принимать равным:
|
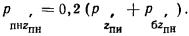
|
(8)
|
При определении осадки с
использованием схемы линейно-деформируемого слоя за расчетную глубину сжимаемой
толщи при повторных нагрузках может быть принята величина, определяемая по п.
2.6, если она меньше z'.
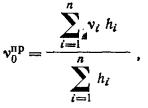
2.16. Осредненный в
пределах сжимаемого слоя Н коэффициент
бокового расширения грунта μср
определяют по формуле
где
μi - коэффициент бокового расширения
i-го
слоя грунта;
hi
- толщина i-го слоя грунта;
n - число слоев грунта, различающихся по сжимаемости в
пределах сжимаемого слоя Н.
При этом коэффициент бокового расширения
следует принимать для крупнообломочного грунта 0,27; песков и супесей - 0,3;
суглинков - 0,35; глин - 0,42.
Осредненный по площади фундамента и
приведенный в пределах сжимаемой толщи Н модуль деформации основания 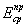 определяют по
указаниям пп.
2.24 и 2.25
настоящего Руководства. определяют по
указаниям пп.
2.24 и 2.25
настоящего Руководства.
2.17. Осадки определяют от нагрузки, равномерно
распределенной по поверхности основания в пределах плана фундамента с
использованием расчетной схемы оснований в виде линейно-деформируемого слоя
методом послойного суммирования осадок отдельных слоев грунта в пределах
сжимаемой толщи Н.
Принимают, что осадка вызывается полным
давлением, передаваемым фундаментом (без вычета природного давления).
Для получения полного представления о
характере деформированной поверхности основания (особенно в случае неоднородного
по сжимаемости в плане основания, а также при необходимости учета влияния
соседних фундаментов или нагрузок на прилегающие площади) осадки основания
следует определять в узлах qf сетки,
наносимой на план фундамента (рис. 3).

Рис.
3. Схема плитного фундамента для расчета осадок неоднородного основания
Рij - нагрузки на колонны; i, j - номера рядов сетки колонн; q, f - номера сторон прямоугольной
сетки для расчета осадок основания; х0,
y0, x1, y1, х2, y2 - системы
координат; ∆х, ∆у - шаг основной сетки; Скв 1 - Скв 5
- геологические скважины
Минимальное количество узлов qf сетки намечают с учетом геологического строения
площадки. Эта сетка должна включать продольные и поперечные стороны
прямоугольного и край круглого фундамента, а также прямые, проходящие через
середины противоположных сторон прямоугольного или через два взаимно
перпендикулярных диаметра круглого фундамента.
2.18. При расчете осадок
прямоугольного плитного фундамента методом послойного суммирования вертикальные
давления 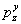 в грунте на глубине z от подошвы
фундамента по вертикали, проходящей через угловую точку фундамента, определяют
по формуле в грунте на глубине z от подошвы
фундамента по вертикали, проходящей через угловую точку фундамента, определяют
по формуле
где
р -
среднее фактическое давление под подошвой фундамента;
H -
толщина сжимаемого слоя основания;
α - коэффициент, учитывающий уменьшение вертикального
давления на нижней границе сжимаемого слоя (на глубине z = H),
принимаемый по табл. 2 в зависимости от отношения длины к ширине фундамента n = l/b и относительной толщины сжимаемого слоя m =2Н/b.
Вертикальные давления pz0 в грунте по вертикали, проходящей через центр
прямоугольного фундамента, вычисляют по формуле
Осадки круглого
фундамента определяют по вертикальным давлениям в грунте, найденным для
квадратного фундамента, эквивалентного по площади круглому.
Таблица 2
|
m' = 2H/b
|
Коэффициент α для фундаментов с
отношением сторон n = l/b, равным:
|
|
1
|
1,2
|
1,4
|
1,6
|
1,8
|
2
|
2,2
|
2,4
|
2,6
|
2,8
|
3
|
3,2
|
3,4
|
3,6
|
4
|
|
0
|
0,25
|
0,25
|
0,25
|
0,25
|
0,25
|
0,25
|
0,25
|
0,25
|
0,25
|
0,25
|
0,25
|
0,25
|
0,25
|
0,25
|
0,25
|
|
0,2
|
0,248
|
0,2479
|
0,2477
|
0,2475
|
0,2473
|
0,2471
|
0,2472
|
0,2472
|
0,2472
|
0,2472
|
0,2471
|
0,247
|
0,2471
|
0,2471
|
0,2471
|
|
0,4
|
0,2456
|
0,2456
|
0,2458
|
0,2461
|
0,2462
|
0,2464
|
0,2465
|
0,2464
|
0,2465
|
0,2464
|
0,2464
|
0,2463
|
0,2463
|
0,2463
|
0,2462
|
|
0,6
|
0,2462
|
0,2462
|
0,2459
|
0,2457
|
0,2458
|
0,2459
|
0,246
|
0,2466
|
0,2462
|
0,2463
|
0,2465
|
0,2466
|
0,2465
|
0,2466
|
0,2464
|
|
0,8
|
0,2378
|
0,2412
|
0,2422
|
0,242
|
0,2421
|
0,2419
|
0,2417
|
0,2417
|
0,2419
|
0,2419
|
0,2420
|
0,2421
|
0,2421
|
0,2421
|
0,2422
|
|
1
|
0,2197
|
0,2274
|
0,2303
|
0,2325
|
0,2328
|
0,2327
|
0,2327
|
0,2325
|
0,2324
|
0,2325
|
0,2323
|
0,2325
|
0,2327
|
0,2327
|
0,2326
|
|
1,2
|
0,1969
|
0,2081
|
0,2153
|
0,2176
|
0,2192
|
0,22
|
0,2202
|
0,2202
|
0,2203
|
0,2202
|
0,2201
|
0,2198
|
0,2199
|
0,2197
|
0,22
|
|
1,4
|
0,1747
|
0,1867
|
0,1971
|
0,2132
|
0,2033
|
0,2052
|
0,206
|
0,2065
|
0,2065
|
0,2064
|
0,2064
|
0,2065
|
0,2065
|
0,2062
|
0,2062
|
|
1,6
|
0,1521
|
0,166
|
0,178
|
0,1823
|
0,1822
|
0,1894
|
0,1909
|
0,192
|
0,1924
|
0,1926
|
0,1929
|
0,1929
|
0,1929
|
0,1928
|
0,1927
|
|
1,8
|
0,1324
|
0,147
|
0,1574
|
0,165
|
0,1702
|
0,1737
|
0,1761
|
0,1776
|
0,1787
|
0,1794
|
0,1797
|
0,1799
|
0,1799
|
0,1798
|
0,1798
|
|
2
|
0,1162
|
0,1299
|
0,1405
|
0,1486
|
0,1545
|
0,1591
|
0,162
|
0,1641
|
0,1656
|
0,1664
|
0,1672
|
0,1675
|
0,1676
|
0,1677
|
0,1679
|
|
2,2
|
0,1012
|
0,115
|
0,126
|
0,1339
|
0,1402
|
0,1451
|
0,1487
|
0,1513
|
0,1532
|
0,1546
|
0,1552
|
0,1562
|
0,1563
|
0,1566
|
0,1571
|
|
2,4
|
0,0899
|
0,102
|
0,1124
|
0,1207
|
0,1273
|
0,1368
|
0,1358
|
0,1394
|
0,1416
|
0,1434
|
0,1445
|
0,1455
|
0,1461
|
0,1465
|
0,1470
|
|
2,6
|
0,0796
|
0,091
|
0,1008
|
0,1088
|
0,1157
|
0,1208
|
0,125
|
0,1285
|
0,1309
|
0,133
|
0,1345
|
0,1356
|
0,1364
|
0,1371
|
0,1377
|
|
2,8
|
0,0703
|
0,0814
|
0,0906
|
0,0984
|
0,105
|
0,1101
|
0,1148
|
0,1204
|
0,1211
|
0,1235
|
0,1253
|
0,1265
|
0,1276
|
0,1284
|
0,1295
|
|
3
|
0,0631
|
0,0731
|
0,0817
|
0,0894
|
0,0957
|
0,101
|
0,1055
|
0,1092
|
0,1124
|
0,1147
|
0,1166
|
0,1181
|
0,1194
|
0,1203
|
0,1215
|
|
3,2
|
0,0568
|
0,066
|
0,0739
|
0,0812
|
0,0945
|
0,0926
|
0,0933
|
0,1008
|
0,1047
|
0,1066
|
0,1087
|
0,1105
|
0,1119
|
0,1129
|
0,1144
|
|
3,4
|
0,0512
|
0,0622
|
0,0673
|
0,0741
|
0,0954
|
0,085
|
0,0895
|
0,0933
|
0,0966
|
0,0991
|
0,1014
|
0,1033
|
0,1048
|
0,1060
|
0,1078
|
|
3,6
|
0,0464
|
0,0538
|
0,0613
|
0,0677
|
0,0734
|
0,0784
|
0,0826
|
0,0864
|
0,0898
|
0,0924
|
0,0966
|
0,0967
|
0,0987
|
0,1008
|
0,1017
|
|
3,8
|
0,0421
|
0,0495
|
0,0559
|
0,0609
|
0,0674
|
0,0723
|
0,076
|
0,0802
|
0,0834
|
0,0862
|
0,0886
|
0,0906
|
0,0923
|
0,0938
|
0,0961
|
|
4
|
0,0385
|
0,0452
|
0,0513
|
0,0570
|
0,0622
|
0,0666
|
0,071
|
0,0752
|
0,0778
|
0,0807
|
0,0833
|
0,0849
|
0,0868
|
0,0883
|
0,0908
|
2.19. Распределение по
глубине вертикальных давлений в любой точке основания в пределах и за пределами
плитного фундамента от приложенных к фундаменту нагрузок, а также от влияния
соседних фундаментов устанавливают методом угловых точек вручную либо на ЭВМ с
помощью программного комплекса «GEST-82», сведения о
котором даны в прил. 1.
В соответствии с методом угловых точек
нормальное давление  по вертикали, проходящей через точку В (рис. 4), определяют по
алгебраическим суммированием давлений по вертикали, проходящей через точку В (рис. 4), определяют по
алгебраическим суммированием давлений 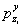 в угловых точках четырех фиктивных фундаментов, равномерно
загруженных давлением р в угловых точках четырех фиктивных фундаментов, равномерно
загруженных давлением р
|

|
(12)
|

Рис. 4. Схема расположения «фиктивных
фундаментов» для определения вертикальных давлений в основании рассчитываемого
фундамента по методу угловых точек
I - схема взаимного
расположения рассчитываемого (1) и влияющего (2) фундаментов;
II - схемы расположения
«фиктивных фундаментов» с указанием знаков давлений в угловых точках основания;
В - точка, через которую
проводят расчетную вертикаль и определяют давления на глубине z по этой вертикали
2.20. Вертикальные
давления р'z на любой глубине по вертикали, проходящей через
рассматриваемую точку фундамента, с учетом соседних фундаментов определяют по
формуле
|
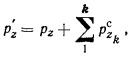
|
(13)
|
где
рz - давление на глубине z от среднего давления р, передаваемого рассчитываемым фундаментом;
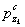 - давление на глубине z под
рассчитываемым фундаментом от влияния соседнего фундамента; - давление на глубине z под
рассчитываемым фундаментом от влияния соседнего фундамента;
k - число влияющих фундаментов.
2.21. При послойном
суммировании осадок определяют вертикальное давление на границе каждого
литологического слоя грунта. Условное разделение этих слоев на более мелкие
слои не требуется в связи с тем, что формулы (10)
и (11) даны для трапецеидальной эпюры
распределения вертикальных давлений.
2.22. Для каждой расчетной
вертикали qf,
проходящей через узел сетки (см. рис.
3), вычисляют приведенный в пределах сжимаемого слоя Н модуль деформации основания 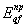 : :
где
n - число литологических слоев
грунта, находящихся в пределах сжимаемой толщи основания по вертикали qf;
hi -
толщина i-го слоя грунта;
рi - среднее давление в i-том слое грунта, равное
полусумме давлений на верхней и нижней границах этого слоя, определяемых по
указаниям пп.
2.18 и 2.19
без учета влияния соседних фундаментов;
Ei - модуль деформации i-гo слоя грунта.
2.23. Степень изменчивости
сжимаемости основания в плане определяют как отношение наибольшего значения приведенного по расчетным
вертикалям модуля деформации грунтов  к наименьшему к наименьшему 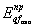 : :
|
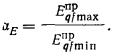
|
(15)
|
Основание считают однородным по
сжимаемости в плане, если αЕ
≤ 1,5.
2.24. Осредненный
приведенный модуль деформации неоднородного в плане основания 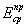 определяют как
отношение к площади фундамента суммы приведенных в соответствии с пп. 2.22 по расчетным вертикалям qf модулей деформации
грунтов определяют как
отношение к площади фундамента суммы приведенных в соответствии с пп. 2.22 по расчетным вертикалям qf модулей деформации
грунтов 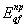 , умноженных на площадь прилегающих к вертикалям qf участков основания. , умноженных на площадь прилегающих к вертикалям qf участков основания.
2.25. Осредненный приведенный модуль деформации однородного
в плане основания 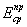 , принимают равным модулю деформации грунтов , принимают равным модулю деформации грунтов 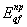 , приведенному в соответствии с пн. 2.22 по вертикали qf, проходящей через
центр подошвы фундамента, при осредненных в пределах плана плиты толщинах слоев
грунта. , приведенному в соответствии с пн. 2.22 по вертикали qf, проходящей через
центр подошвы фундамента, при осредненных в пределах плана плиты толщинах слоев
грунта.
2.26. Осадку Sqf точки qf поверхности основания фундамента по методу послойного
суммирования определяют (с учетом и без учета влияния соседних фундаментов) по
формуле
где
pi - среднее давление в i-том слое
грунта, равное полусумме давлений на верхней и нижней границах этого слоя,
определяемых с учетом либо без учета влияния соседних фундаментов по указаниям пп.
2.18 - 2.20;
mг - коэффициент условий работы основания, нагруженного
по большой площади, принимаемый для оснований с осредненный приведенным модулем
деформации 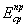 ≥ 10 МПа в
зависимости от ширины b прямоугольного
или диаметра b = 2r круглого фундамента равным: mг = 1,35 при 10 м < b ≤ 15 м и mг = 1,5
при b > 15 м; mг = 1,
если осредненный приведенный модуль деформации основания ≥ 10 МПа в
зависимости от ширины b прямоугольного
или диаметра b = 2r круглого фундамента равным: mг = 1,35 при 10 м < b ≤ 15 м и mг = 1,5
при b > 15 м; mг = 1,
если осредненный приведенный модуль деформации основания  < 10 МПа; < 10 МПа;
β - безразмерный коэффициент, равный 0,8.
2.27. Среднюю
осадку неоднородного в плане основания находят как отношение к площади
фундамента суммы осадок Sqf основания в точках qf, умноженных на площадь примыкающих к этим точкам
участков основания.
2.28. Среднюю осадку неоднородного по глубине и однородного
в плане основания прямоугольного или круглого плитного фундамента вычисляют по
формуле
где
b - ширина прямоугольного или диаметр круглого
фундамента;
р - среднее
давление на грунт под подошвой фундамента;
М - поправочной
коэффициент, принимаемый в зависимости от отношения толщины сжимаемого слоя H к
полуширине прямоугольного m' = 2Н/b или радиусу
круглого m'
= Н/r фундамента равным: M = 1,5 при
0 < m' ≤ 0,5; М
= 1,4 при 0,5 < m' ≤ 1; М
= 1,3 при 1 < m '≤ 2; M = l,2 при 2 < m' ≤
3; М = 1,1 при 3 < m' ≤ 5
и М = 1 при m '>
5;
n - количество слоев грунта, различающихся по
сжимаемости в пределах линейно-деформируемого слоя Н;
ki - коэффициент, определяемый по
табл. 3 в зависимости от формы подошвы фундамента, отношения сторон
прямоугольного фундамента n = l/b, а также отношения глубины z залегания подошвы слоя к полуширине прямоугольного m' = 2z/b или радиусу круглого m' = z/r фундамента;
mг - коэффициент условий работы основания, нагруженного
по большой площади, определяемый по п.
2.26;
Ei - модуль деформации i-го слоя грунта.
2.29. Осадки
однородного в плане основания под центром, угловыми точками и серединами сторон
прямоугольного фундамента определяют по формуле
где
р - среднее давление на основание под подошвой
фундамента;
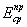 - осредненный приведенный модуль деформации основания,
определяемый по пп.
2.24 и 2.25; - осредненный приведенный модуль деформации основания,
определяемый по пп.
2.24 и 2.25;
k = k0 - коэффициент, определяемый по табл. 4 для точки
основания под центром фундамента в зависимости от отношения сторон фундамента n = l/b и отношения толщины сжимаемого слоя к полуширине
фундамента m'
= 2H/b;
k = k1 - то же, под серединой большей стороны фундамента;
k = k2- коэффициент, определяемый по табл. 4 для точки
основания под серединой меньшей стороны фундамента в зависимости от отношения
сторон фундамента n = l/b и отношения толщины сжимаемого слоя Н к полуширине фундамента m' = 2H/b;
k = k3 -то же, под угловой точкой фундамента.
Таблица 3
|
m' = 2z/b
m' = z/r
|
Коэффициент
ki
для фундаментов
|
|
круглых
радиусом
r
|
прямоугольных
с соотношением сторон n = l/b, равным
|
ленточных
n > 10
|
|
1
|
1,4
|
1,8
|
2,4
|
3,2
|
5
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0,4
|
0,090
|
0,100
|
0,100
|
0,100
|
0,100
|
0,100
|
0,100
|
0,104
|
|
0,8
|
0,179
|
0,200
|
0,200
|
0,200
|
0,200
|
0,200
|
0,200
|
0,208
|
|
1,2
|
0,266
|
0,299
|
0,300
|
0,300
|
0,300
|
0,300
|
0,300
|
0,311
|
|
1,6
|
0,348
|
0,380
|
0,394
|
0,397
|
0,397
|
0,397
|
0,397
|
0,412
|
|
2
|
0,411
|
0,446
|
0,472
|
0,482
|
0,486
|
0,486
|
0,486
|
0,511
|
|
2,4
|
0,461
|
0,499
|
0,538
|
0,556
|
0,565
|
0,567
|
0,567
|
0,605
|
|
2,8
|
0,501
|
0,542
|
0,592
|
0,618
|
0,635
|
0,640
|
0,640
|
0,687
|
|
3,2
|
0,532
|
0,577
|
0,637
|
0,671
|
0,696
|
0,707
|
0,709
|
0,763
|
|
3,6
|
0,558
|
0,606
|
0,676
|
0,717
|
0,750
|
0,768
|
0,772
|
0,831
|
|
4
|
0,579
|
0,600
|
0,708
|
0,756
|
0,796
|
0,820
|
0,830
|
0,892
|
|
4,4
|
0,596
|
0,650
|
0,735
|
0,789
|
0,837
|
0,867
|
0,883
|
0,949
|
|
4,8
|
0,611
|
0,668
|
0,759
|
0,819
|
0,873
|
0,908
|
0,932
|
1,001
|
|
5,2
|
0,624
|
0,683
|
0,780
|
0,884
|
0,904
|
0,948
|
0,977
|
1,005
|
|
5,6
|
0,635
|
0,697
|
0,798
|
0,867
|
0,933
|
0,981
|
1,018
|
1,095
|
|
6
|
0,645
|
0,708
|
0,814
|
0,887
|
0,958
|
1,011
|
1,056
|
1,138
|
|
6,4
|
0,653
|
0,719
|
0,828
|
0,904
|
0,980
|
1,031
|
1,090
|
1,178
|
|
6,8
|
0,661
|
0,728
|
0,841
|
0,920
|
1
|
1,065
|
1,122
|
1,215
|
|
7,2
|
0,668
|
0,736
|
0,852
|
0,935
|
1,019
|
1,088
|
1,152
|
1,251
|
|
7,6
|
0,674
|
0,744
|
0,863
|
0,948
|
1,036
|
1,109
|
1,180
|
1,285
|
|
8
|
0,679
|
0,751
|
0,872
|
0,960
|
1,051
|
1,128
|
1,205
|
1,316
|
|
8,4
|
0,684
|
0,757
|
0,881
|
0,970
|
1,065
|
1,146
|
1,229
|
1,347
|
|
8,8
|
0,689
|
0,762
|
0,888
|
0,980
|
1,078
|
1,162
|
1,251
|
1,376
|
|
9,2
|
0,693
|
0,768
|
0,896
|
0,989
|
1,089
|
1,178
|
1,272
|
1,404
|
|
9,6
|
0,697
|
0,772
|
0,902
|
0,998
|
1,100
|
1,192
|
1,291
|
1,431
|
|
10
|
0,700
|
0,777
|
0,908
|
1,005
|
1,110
|
1,205
|
1,309
|
1,456
|
|
11
|
0,705
|
0,786
|
0,922
|
1,022
|
1,132
|
1,233
|
1,349
|
1,506
|
|
12
|
0,710
|
0,794
|
0,933
|
1,037
|
1,151
|
1,257
|
1,384
|
1,550
|
Таблица
4
|
m' = 2H/b
|
n = 1
|
n = 1,5
|
n = 2
|
|
k0
|
k1
|
k2
|
k3
|
k0
|
k1
|
k2
|
k3
|
k0
|
|
0,2
|
0,090
|
0,045
|
0,045
|
0,024
|
0,091
|
0,046
|
0,045
|
0,024
|
0,091
|
|
0,5
|
0,233
|
0,115
|
0,115
|
0,056
|
0,229
|
0,113
|
0,115
|
0,056
|
0,229
|
|
1
|
0,462
|
0,233
|
0,233
|
0,116
|
0,469
|
0,235
|
0,231
|
0,115
|
0,466
|
|
2
|
0,701
|
0,398
|
0,398
|
0,233
|
0,769
|
0,443
|
0,404
|
0,230
|
0,796
|
|
3
|
0,802
|
0,485
|
0,485
|
0,309
|
0,911
|
0,565
|
0,508
|
0,323
|
0,969
|
|
5
|
0,888
|
0,565
|
0,565
|
0,380
|
1,036
|
0,682
|
0,617
|
0,426
|
1,130
|
|
7
|
0,925
|
0,601
|
0,601
|
0,416
|
1,092
|
0,736
|
0,669
|
0,478
|
1,204
|
|
10
|
0,954
|
0,630
|
0,630
|
0,444
|
1,135
|
0,779
|
0,712
|
0,518
|
1,260
|
Продолжение табл. 4
|
m' = 2H/b
|
n = 2
|
n = 3
|
n = 5
|
|
k1
|
k2
|
k3
|
k0
|
k1
|
k2
|
k3
|
k0
|
|
0,2
|
0,046
|
0,045
|
0,023
|
0,092
|
0,047
|
0,046
|
0,023
|
0,092
|
|
0,5
|
0,112
|
0,114
|
0,056
|
0,229
|
0,112
|
0,115
|
0,056
|
0,230
|
|
1
|
0,233
|
0,231
|
0,115
|
0,463
|
0,229
|
0,231
|
0,114
|
0,461
|
|
2
|
0,461
|
0,403
|
0,233
|
0,808
|
0,469
|
0,400
|
0,328
|
0,802
|
Продолжение табл. 4
|
m' = 2H/b
|
n = 2
|
n = 3
|
n = 5
|
|
k1
|
k2
|
k3
|
k0
|
k1
|
k2
|
k3
|
k0
|
|
3
|
0,610
|
0,514
|
0,328
|
1,016
|
0,649
|
0,514
|
0,328
|
1,029
|
|
5
|
0,761
|
0,641
|
0,448
|
1,235
|
0,852
|
0,658
|
0,462
|
1,305
|
|
7
|
0,832
|
0,708
|
0,512
|
1,340
|
0,954
|
0,742
|
0,545
|
1,459
|
|
10
|
0,888
|
0,762
|
0,565
|
1,423
|
1,036
|
0,815
|
0,616
|
1,588
|
Продолжение табл. 4
|
m' = 2H/b
|
n = 5
|
n = 10
|
|
k1
|
k2
|
k3
|
k0
|
k1
|
k2
|
k3
|
|
0,2
|
0,047
|
0,046
|
0,024
|
0,091
|
0,047
|
0,046
|
0,024
|
|
0,5
|
0,114
|
0,115
|
0,057
|
0,231
|
0,114
|
0,115
|
0,057
|
|
1
|
0,229
|
0,231
|
0,114
|
0,463
|
0,230
|
0,232
|
0,115
|
|
2
|
0,464
|
0,400
|
0,231
|
0,799
|
0,461
|
0,400
|
0,231
|
|
3
|
0,658
|
0,511
|
0,326
|
1,023
|
0,651
|
0,511
|
0,326
|
|
5
|
0,916
|
0,658
|
0,463
|
1,316
|
0,926
|
0,656
|
0,460
|
|
7
|
1,065
|
0,756
|
0,558
|
1,511
|
1,116
|
0,752
|
0,555
|
|
10
|
1,193
|
0,852
|
0,652
|
1,706
|
1,306
|
0,868
|
0,659
|
2.30. Осадки однородного основания прямоугольного
фундамента от влияния соседнего прямоугольного фундамента или нагрузок на
прилегающие прямоугольные площади определяют как алгебраические суммы осадок
соответствующих точек основания прямоугольных «фиктивных фундаментов» (рис.
4) с использованием формулы (18).
2.31. Осадки точек поверхности однородного основания
круглого фундамента радиусом r определяют по формуле
|
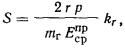
|
(19)
|
где
р - среднее давление на основание под подошвой
фундамента;
kr
= коэффициент, принимаемый по табл. 5 в
зависимости от отношения толщины слоя Н к радиусу фундамента m' = Н/r и отношения p = ri/r (здесь ri - расстояние от центра фундамента до рассматриваемой
точки i поверхности основания);
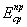 - осредненный приведенный модуль деформации
основания, определяемый по п.
2.25. - осредненный приведенный модуль деформации
основания, определяемый по п.
2.25.
Осадки различных точек непрямоугольного
фундамента (приводимого к системе прямоугольников) допускается определять как
алгебраические суммы осадок соответствующих точек основания прямоугольных
фундаментов, на которые условно разбивают непрямоугольный фундамент. При этом
используется метод, изложенный в п. 2.30.
Осадки прямоугольных и круглых
фундаментов на однородном основании приближенно можно определить по графикам прил. 2
и 3.
Таблица 5
|
m' = H/r
|
Значение
kr при p = ri/r равном
|
|
0
|
0,25
|
0,5
|
0,75
|
1
|
1,25
|
1,5
|
2
|
2,5
|
3
|
4
|
5
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0,25
|
0,12
|
0,12
|
0,12
|
0,12
|
0,05
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
0,5
|
0,24
|
0,24
|
0,23
|
0,22
|
0,11
|
0
|
-
|
-
|
-
|
-
|
-
|
-
|
|
0,75
|
0,35
|
0,35
|
0,34
|
0,29
|
0,16
|
0,03
|
0,01
|
-
|
-
|
-
|
-
|
-
|
|
1
|
0,45
|
0,44
|
0,42
|
0,35
|
0,21
|
0,07
|
0,02
|
0
|
-
|
-
|
-
|
-
|
|
1,5
|
0,58
|
0,57
|
0,53
|
0,45
|
0,28
|
0,13
|
0,07
|
0,02
|
0
|
-
|
-
|
-
|
|
2
|
0,65
|
0,64
|
0,60
|
0,52
|
0,34
|
0,17
|
0,10
|
0,04
|
0,01
|
0
|
-
|
-
|
|
3
|
0,74
|
0,73
|
0,68
|
0,59
|
0,41
|
0,23
|
0,16
|
0,08
|
0,04
|
0,02
|
0
|
-
|
|
4
|
0,81
|
0,79
|
0,74
|
0,66
|
0,47
|
0,30
|
0,22
|
0,13
|
0,09
|
0,06
|
0,02
|
0,01
|
|
5
|
0,84
|
0,82
|
0,77
|
0,69
|
0,50
|
0,33
|
0,24
|
0,15
|
0,11
|
0,08
|
0,04
|
0,02
|
|
7
|
0,85
|
0,83
|
0,79
|
0,71
|
0,52
|
0,35
|
0,27
|
0,18
|
0,13
|
0,10
|
0,06
|
0,04
|
|
10
|
0,91
|
0,89
|
0,84
|
0,76
|
0,58
|
0,40
|
0,32
|
0,25
|
0,18
|
0,15
|
0,11
|
0,09
|
2.32. Осадки основания силосных корпусов следует определять
с учетом многократно повторного характера приложения нагрузки от загружаемого
продукта.
Дополнительные осадки основания силосного
корпуса, вызванные многократно повторными нагрузками от веса загружаемого
продукта, находят с учетом сжимаемой толщи, вычисляемой по п.
2.15.
2.33. Крен фундамента от действия внецентренной нагрузки
(изгибающего момента в уровне подошвы фундамента) вычисляют:
а) прямоугольного фундамента -
в направлении большей его стороны l (вдоль
продольной оси) по формуле
|
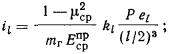
|
(20)
|
б) прямоугольного фундамента -
в направлении меньшей его стороны (вдоль поперечной оси) по формуле
|

|
(21)
|
в) круглого фундамента
радиусом r по формуле
|

|
(22)
|
где
Р -
равнодействующая всех вертикальных нагрузок от фундамента на основание;
el, eb, e - соответственно расстояния точки приложения
равнодействующей от середины подошвы фундамента до продольной оси, поперечной
оси и по радиусу круга;
μср и 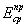 - соответственно
осредненный коэффициент бокового расширения грунта и осредненный приведенный
модуль деформации основания, принимаемые по пп.
2.16, 2.24,
2.25; - соответственно
осредненный коэффициент бокового расширения грунта и осредненный приведенный
модуль деформации основания, принимаемые по пп.
2.16, 2.24,
2.25;
kl и kb - коэффициенты, определяемые по табл. 6 и 7 в
зависимости от отношения сторон подошвы фундамента n = l/b и отношения толщины сжимаемого слоя Н к полуширине фундамента m' = 2H/b;
k1 - коэффициент, определяемый по табл. 8 в зависимости
от отношения толщины линейно-деформируемого слоя Н к радиусу r круглого фундамента m' = Н/r.
Таблица
6
|
n = l/b
|
Значения
kl при m' = 2H/b, равном
|
|
0,5
|
1
|
1,5
|
2
|
3
|
4
|
5
|
|
1
|
0,28
|
0,41
|
0,46
|
0,48
|
0,5
|
0,5
|
0,5
|
|
1,2
|
0,29
|
0,44
|
0,51
|
0,54
|
0,57
|
0,57
|
0,57
|
|
1,5
|
0,31
|
0,48
|
0,57
|
0,62
|
0,66
|
0,68
|
0,68
|
|
2
|
0,32
|
0,52
|
0,64
|
0,72
|
0,78
|
0,81
|
0,82
|
|
3
|
0,33
|
0,56
|
0,73
|
0,83
|
0,95
|
1,01
|
1,04
|
|
5
|
0,34
|
0,60
|
0,81
|
0,95
|
1,12
|
1,24
|
1,31
|
|
10
|
0,35
|
0,63
|
0,85
|
1,05
|
1,31
|
1,46
|
1,57
|
Таблица
7
|
n = l/b
|
Значения
kb при m' = 2H/b, равном
|
|
0,5
|
1
|
1,5
|
2
|
3
|
4
|
5
|
|
1
|
0,28
|
0,41
|
0,46
|
0,48
|
0,5
|
0,5
|
0,5
|
|
1,2
|
0,24
|
0,35
|
0,39
|
0,41
|
0,42
|
0,43
|
0,43
|
|
1,5
|
0,2
|
0,28
|
0,32
|
0,33
|
0,36
|
0,36
|
0,36
|
|
2
|
0,15
|
0,22
|
0,25
|
0,27
|
0,28
|
0,28
|
0,28
|
|
3
|
0,1
|
0,15
|
0,17
|
0,18
|
0,19
|
0,19
|
0,19
|
|
5
|
0,06
|
0,09
|
0,1
|
0,11
|
0,12
|
0,12
|
0,12
|
|
10
|
0,03
|
0,05
|
0,05
|
0,06
|
0,06
|
0,06
|
0,06
|
Таблица
8
|
m'
|
0,25
|
0,5
|
1
|
2
|
> 3
|
|
k1
|
0,26
|
0,43
|
0,63
|
0,74
|
0,75
|
2.34. Крены плитного
фундамента, вызванные неоднородностью основания в плане либо влиянием соседнего
фундамента, определяют как отношение разности средних осадок противоположных
сторон фундамента к расстоянию между ними, т.е. к длине, либо к ширине
прямоугольного фундамента и к диаметру круглого фундамента.
Крены прямоугольного фундамента, осадки Sqf неоднородного основания которого найдены в узлах qf прямоугольной сетки, нанесенной на план фундамента с
шагом ∆х в
продольном направлении и ∆у
в поперечном направлении, можно определить по формулам:
а) в направлении большей стороны
|
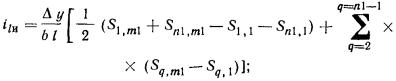
|
(23)
|
б) в направлении меньшей стороны
|
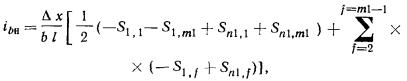
|
(24)
|
где
q -
номер ряда узлов сетки, параллельного
длинной стороне фундамента (q = 1, 2, 3,…, n1);
f -
номер ряда узлов сетки, параллельного
короткой стороне фундамента (f = l, 2, 3,..., m1).
Аналогично определяют крен прямоугольного
фундамента от влияния соседнего фундамента.
2.35. Крен фундамента многоэтажного здания или сооружения
башенного типа следует определять с учетом увеличения эксцентриситета
приложения вертикальной составляющей нагрузки вследствие наклона фундамента или
здания (сооружения) в целом. Кроме того, как правило, нужно учитывать
увеличение эксцентриситета нагрузки за счет податливости надфундаментной
конструкции.
Дополнительный крен фундамента
многоэтажного здания, вызванный увеличением эксцентриситета приложения
вертикальной нагрузки при наклоне здания в целом, без учета податливости
надфундаментной конструкции определяют в случае:
а) однородного основания по
формуле
|

|
(25)
|
где
i - крен фундамента, определяемый по указаниям п.
2.33 в зависимости от принятой расчетной схемы основания, характеристик его
сжимаемости, формы и размеров фундамента, а также направления действия
суммарного изгибающего момента М
в уровне подошвы фундамента;
 - крен фундамента от единичного изгибающего момента; - крен фундамента от единичного изгибающего момента;
Р - вертикальная составляющая всей нагрузки,
действующей на фундамент;
h' - высота от подошвы фундамента до точки приложения
нагрузки Р;
б) неоднородного основания по
формуле
где
iн - крен фундамента вследствие неоднородности
основания, определяемый по указаниям п.
2.34.
Остальные обозначения те же, что и в
формуле (25).
2.36. Суммарный крен фундамента, найденный по пп.
2.33, 2.34,
не должен превышать предельных величин, установленных главой СНиП на
проектирование основания зданий и сооружений.
2.37. Крен фундаментов
силосных корпусов определяют с учетом повышения модуля деформации основания
вследствие предварительного обжатия грунта равномерной загрузкой длительностью
не менее 2 мес. Коэффициент увеличения модуля деформации основания находят по
табл. 9 в зависимости от наименования грунтов.
Таблица
9
|
Наименование
грунтов
|
Коэффициент
К0
|
Наименование
грунтов
|
Коэффициент
К0
|
|
Песчаные
грунты
|
1,5
|
Глинистые
грунты тугопластичной консистенции
|
1,2
|
|
Глинистые
грунты твердой н полутвердой консистенции
|
1,3
|
Прочие грунты
|
1
|
2.38. Крены прямоугольных и круглых фундаментов на
однородном основании можно приближенно найти по графикам прил. 2
и 3.
Пример расчета деформаций основания.
Требуется рассчитать основание плитного
фундамента четырех сблокированных монолитных железобетонных силосных корпусов.
Геологический разрез и план плитного
фундамента приведены на рис. 5.
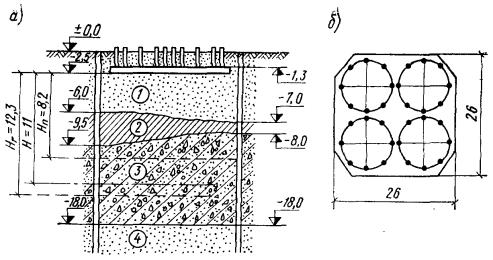
Рис. 5. Пример расчета деформаций основания
а - геологический разрез; б - план плитного фундамента; 1 - песок
средней крупности; 2 -
суглинок; 3 - мореный суглинок;
4 - песок мелкий
Расчетные характеристики грунтов
основания определены по данным табл. 1 и 2 прил. 2 к главе СНиП на
проектирование оснований зданий и сооружений и приведены в табл. 10.
Таблица
10
|
Наименование
грунтов
|
Толщина
слоя грунта, м
|
Характеристика
грунтов
|
|
cII
кПа
|
φII
град
|
е
|
Il
|
γII
т/м3
|
е,
МПа
|
μ
|
|
Песок средней
крупности
|
3,5-4,5
|
3
|
40
|
0,45
|
-
|
1,75
|
33
|
0,3
|
|
Суглинок
мягко-пластичный
|
1-3,5
|
25
|
19
|
0,65
|
0,6
|
2
|
11
|
0,36
|
|
Суглинок
моренный
|
8,5
|
47
|
26
|
0,45
|
0,1
|
2
|
37
|
0,35
|
|
Песок мелкий
|
-
|
6
|
38
|
0,45
|
-
|
1,75
|
32
|
0,3
|
Глубина заложения плитного
фундамента h = 2,5 м принята минимальной с
тем, чтобы по возможности не уменьшать толщину песка средней крупности в зоне
наибольших деформаций и уменьшить давление на мягкопластичный суглинок.
На плитный фундамент в уровне его подошвы
передаются следующие расчетные нагрузки (при расчете оснований по деформациям
они равны нормативным):
постоянная от собственного веса всех
силосов G1 = 44200
кН;
временная от загрузки одного силоса P1 = 27000 кН, изгибающий момент от ветровой нагрузки Мв = 46000 кН·м.
При расчете основания по деформациям без
учета совместной работы основания, плитного фундамента и надфундаментного
строения, предельные значения деформаций основания можно принять по табл. 18
главы СНиП на проектирование оснований зданий и сооружений равными: крена - 0,004,
средней осадки - 40 см.
Предварительные минимальные размеры
фундамента в плане принимаем по габаритам надфундаментного строения равными 26
× 26 м и проверяем по указаниям п.
2.2.
Вычисляем среднее давление на грунт от
нормативных нагрузок с учетом веса грунта обратной засыпки:
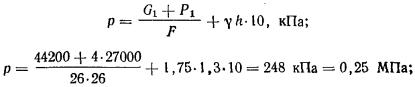
Для определения расчетного давления на
основание предварительно находим следующие величины по табл. 16, 17 и п. 3.52
главы СНиП на проектирование оснований зданий и сооружений: А = 2,46; В = 10,84; D = 11,73; m1 = 1,4; m2 = 1,4 и kн = 1,1.
Расчетное давление на основание
определяем по п. 3.50 той же главы СНиП:

Следовательно, расчет основания можно
вести с использованием теории линейно-деформируемой среды.
Давление под краем фундамента при
загружении двух силосов

т.е. требование п. 3.60 главы СНиП на
проектирование оснований зданий и сооружений удовлетворяется.
Ширина рассчитываемого плитного
фундамента b > 10 и модули деформации грунтов основания E > 10
МПа, поэтому в соответствии с п.
2.10 б для определения деформаций основания используем расчетную схему
линейно-деформируемого слоя.
Толщину линейно-деформируемого слоя Н определяем по указаниям пп.
2.6 и 2.7:
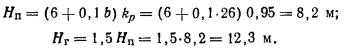
Поскольку в пределах от Hп до Hг залегает
глинистый грунт, величину Н определяем
по формуле (3)
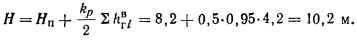
Принимаем (в запас) H = 11 м.
В соответствии с требованием п. 3.62 СНиП
на проектирование оснований зданий и сооружений, проверяем давление на кровлю
слоя мягкопластичного суглинка, расположенную на глубине z = 4 м от
подошвы фундамента.
При

по табл. 2 находим α
= 0,2333.
Давление на глубине z = 4 м под
центром фундамента определяем по формуле (11)
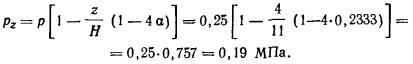
Расчетное давление Rz на кровлю мягкопластичного
суглинка определяем по формуле (17)
вышеуказанной главы СНиП для условного фундамента шириной bz,
равной:

Величины, необходимые для вычисления
давления Rz, равны:
А = 0,47; В = 2,89; D = 5,48; m1 = 1,1; m2 = 1; kн = 1,1.
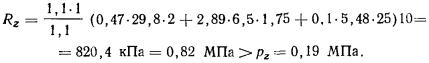
Для определения наибольшего Emax
и наименьшего Emin модулей деформации основания, приведенных по
вертикалям, проходящим через середины противоположных сторон фундамента,
предварительно находим средние давления в слоях грунта, находящихся в пределах
сжимаемой толщи Н.
Поскольку по п.
2.18 эпюра вертикальных давлений имеет вид трапеции, вычисляем средние
давления в пределах каждого из трех слоев грунта под серединами противоположных
сторон фундамента, как давления в середине толщины слоя, по формуле (10) с
введением при коэффициенте α
множителя, равного 2, по методу угловых точек:
а) для левой стороны
фундамента при z1 = 1,75 м
в слое песка средней крупности:

при z2 = 5,25 м
в слое мягкопластичного суглинка
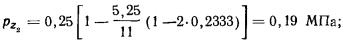
при z3 = 9 м в
слое моренного суглинка
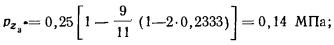
б) для правой стороны:
при z4 = 2,25 м в слое песка средней крупности
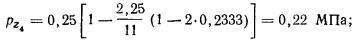
при z5 = 5 м в
слое мягкопластичного суглинка

при z6 = 8,25 м
в слое моренного суглинка
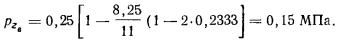
Используя найденные значения рz, вычисляем по формуле (14)
настоящего Руководства приведенные модули деформации основания Emin под серединой левой стороны
фундамента и Еmax под правой:

Оцениваем степень изменчивости
сжимаемости основания в плане в соответствии с указанием п.
2.23

т.е. основание нужно считать неоднородным
по сжимаемости в плане.
Определяем осредненный
приведенный модуль деформации неоднородного основания  по рекомендациям п.
2.24 и с учетом характера напластования грунтов принимаем равным: по рекомендациям п.
2.24 и с учетом характера напластования грунтов принимаем равным:
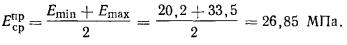
Повышение модуля деформации в
соответствии с п.
2.37 за счет предварительного обжатия грунтов равномерной нагрузкой (от
загрузки силосов) не учитываем из-за наличия в основании слоя мягкопластичного
суглинка.
Средний коэффициент бокового давления
грунта определяем по формуле (9)
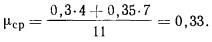
Находим по формуле (16) осадки середин противоположных сторон фундамента с
использованием результатов вычислений, выполненных при определении модулей
деформации Emin и Emax:
а) левой стороны фундамента
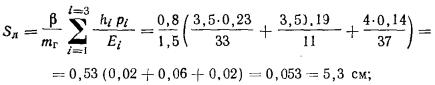
б) правой стороны
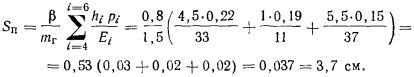
Вычисляем среднюю осадку основания

В соответствии с п. 2.35 при определении
крена плитного фундамента необходимо рассматривать силосный корпус в целом как
сооружение с высокорасположенным центром тяжести и учитывать увеличение
эксцентриситета вертикальной нагрузки из-за наклона сооружения.
Для этого сначала вычисляем крен
фундамента, считая его низким, от внецентренного действия нагрузки (заполнения
двух силосов) и ветровой нагрузки по п.
2.33
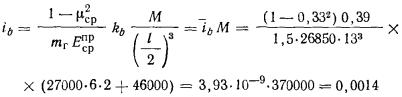
(здесь попутно вычислено значение  , которое потребуется в дальнейших вычислениях). , которое потребуется в дальнейших вычислениях).
Крен фундамента, вызванный
неоднородностью основания, определяем по п.
2.34 как отношение разности осадок середин противоположных сторон
квадратного фундамента к его стороне
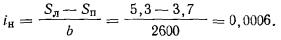
Суммарная нагрузка на основание Р при заполнении двух силосов равна:

Суммарный крен силосного корпуса
определяем по формуле (26):

Таким образом, исходя из расчета
деформаций основания размеры плитного фундамента могут быть приняты равными 26 ×
26 м.
3.
ОПРЕДЕЛЕНИЕ ПРЕДВАРИТЕЛЬНЫХ РАЗМЕРОВ ПЛИТНОГО ФУНДАМЕНТА ПО УСЛОВИЮ
МИНИМАЛЬНОГО ОБЪЕМА БЕТОНА
3.1. Определение предварительных размеров плитного
фундамента выполняют при подготовке исходной информации к совместному расчету
основания, плитного фундамента и надфундаментного строения, а затем уточняют по
результатам статического расчета, так как в большинстве программ статического
расчета плитных фундаментов для сокращения времени счета не предусмотрено
варьирование размеров фундамента.
3.2. Предварительные размеры плитных фундаментов каркасных
зданий и сооружений можно вычислить на ЭВМ по программе «РАПОРТ»,
характеристики которой приведены в прил.
1.
3.3.
При определении предварительных размеров фундамента по условию минимума объема
бетона, близкому для монолитного железобетона к минимуму стоимости варьируют
толщину фундамента, а также размеры в плане и толщину местных монолитных утолщений
под колоннами (банкеток) и стенами.
Размеры фундамента в плане определяют по
габаритам надфундаментного строения с добавлением консольных участков. Размеры
(вылеты) этих участков находят при определении минимальных размеров фундамента
в плане по рекомендациям разд. 2, а затем уточняют по
условиям (27) и (42).
3.4. Размеры фундамента здания или сооружения, для которого установлены ограничения
по разностям осадок соседних колонн или участков фундамента под несущими
стенами, проверяют по этим ограничениям предварительно при подготовке
информации к расчету плитного фундамента на сжимаемом основании и окончательно
по результатам этого расчета.
3.5. Вычисление
предварительных размеров фундамента выполняют методом последовательных
приближений, принимая при этом минимальную и максимальную толщину фундамента по
конструктивным соображениям, а местные утолщения фундамента в пределах от
нулевой до максимальной величины, также определяемой по конструктивным
соображениям.
3.6. При определении
предварительных размеров плитного фундамента каркасного здания или сооружения
толщину фундамента принимают не менее требуемой из расчета прочности на
продавливание бетона (без учета поперечного армирования) базами колонн или
подколонниками с последующим уточнением по результатам проверки прочности
наклонных сечений фундамента без учета поперечного армирования на действие
поперечных сил, величины которых получают при расчете плитного фундамента на
сжимаемом основании.
Участки фундамента в местах расположения
стен жесткости также проверяют по условию прочности наклонных сечений на
действие поперечной силы.
3.7. Толщину плитного
фундамента здания или сооружения с несущими стенами принимают не менее
требуемой из расчета прочности наклонных сечений без учета поперечного
армирования на действие поперечных сил. Величины этих сил при предварительном
расчете прямоугольных плитных фундаментов определяют, принимая основание однородным
в плане с расчетной схемой в виде линейно-деформируемого слоя, параметры
которого находят по указаниям разд. 2.
3.8. Условие прочности плитного фундамента на продавливание
бетона базами колонн или подколонниками (банкетками) без учета поперечной
арматуры принимают в соответствии с указаниями главы СНиП на проектирование
бетонных и железобетонных конструкций в виде зависимости
где
Рп - продавливающая сила, определяемая по формуле
|
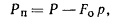
|
(28)
|
здесь
Р - расчетная нагрузка на колонну;
F0 - площадь
нижнего основания пирамиды продавливания;
р - среднее
давление на грунт в пределах нижнего основания пирамиды продавливания от
расчетных нагрузок (для предварительных расчетов р принимают равным отношению расчетной
нагрузки на колонну в уровне верха фундамента к площади фундамента,
определяемой как произведение полусумм расстояний между колоннами, но не более,
чем 6 × 6 м, а затем уточняют по результатам статического расчета);
Rp - расчетное сопротивление бетона на осевое растяжение;
bср -
средний периметр пирамиды продавливания;
h -
рабочая высота сечения плитного фундамента;
kп -
коэффициент, принимаемый равным 1 (для тяжелого бетона).
Расчетные схемы продавливания плитного
фундамента, определяющие величины F0 и bср в формулах (27) и (28), принимают в зависимости от
расположения колонн на фундаменте по наиболее невыгодной из возможных схем
продавливания.
При выборе схемы продавливания плитного
фундамента количество плоскостей продавливания, проходящих через базы колонн
или подколенников, задают равным:
четырем для средних колонн, если
выполняется условие
|

|
(29)
|
где
l - расстояние между осями колонн;
h -
толщина фундамента,
а - длина или ширина сечения колонны или подколонника;
k -
номер колонны;
трем для крайних, а также для двух
средних колонн, расположенных на расстоянии
|

|
(30)
|
двум для угловых, а также для четырех
средних колонн, расположенных на расстоянии l, удовлетворяющем условию (30).
3.9. Минимальные размеры
плитного фундамента, требуемые по условиям (27) и (28), определяют по следующим
зависимостям при продавливании фундамента прямоугольным подколонником:
а)
по четырем граням в средних зонах фундамента
где
h -
толщина фундамента;
а и b' - соответственно ширина и длина подколонника;
с - защитный слой бетона;
б) по трем граням у края
фундамента
где
lk - длина
консоли фундамента от оси крайнего ряда колонн;
в) по двум граням в угловом
участке фундамента:
|


|
(34)
|

Рис. 6. Схема плитного фундамента под сетку
колони для подбора его оптимальных размеров
Pij – нагрузки на
колонны; i, j – номера рядов сетки колонн; x, y – система координат
а + b'
|

|
(35)
|
Формулы (32)
- (35) используют в том случае, когда возможно продавливание фундамента
колоннами крайнего ряда, параллельного короткой стороне плиты. При этом длинную
сторону колонны b' считают параллельной длинной стороне плиты. Если ряд
колонн параллелен длинной стороне плиты, то в формулах (32) - (35) величину b' заменяют на а
и обратно.
По формулам (32)
и (33) можно определить размеры плитного
фундамента для случая близко расположенных средних колонн.
При этом величину lк принимают
равной половине расстояния между осями колонн.
Толщину плитного фундамента и размеры в плане
квадратных подколонников можно найти в зависимости от величины предельной по
продавливанию фундамента нагрузки, кН·10, на колонну по табл. 11, составленной
с использованием формулы (31).
Таблица 11
|
Толщина плиты, м
|
Размер подколенников в плане, м
|
|
0,5
|
1,0
|
1,5
|
2,0
|
|
При среднем давлении на основание 0,1 МПа
для плиты из бетона М 200
|
|
0,4
|
110,5
|
178
|
250,5
|
328
|
|
0,5
|
152,5
|
235
|
322,5
|
415
|
|
0,6
|
200,5
|
298
|
400,5
|
508
|
|
0,7
|
254,5
|
367
|
484,5
|
607
|
|
0,8
|
314,5
|
442
|
574,5
|
712
|
|
0,9
|
380,5
|
523
|
670,5
|
823
|
|
1
|
452,5
|
610
|
772,5
|
940
|
|
1,1
|
530,5
|
703
|
880,5
|
1063
|
|
1,2
|
614,5
|
802
|
994,5
|
1192
|
|
1,3
|
704,5
|
907
|
1114,5
|
1327
|
|
1,4
|
800,5
|
1018
|
1240,5
|
1468
|
|
1,5
|
902,5
|
1135
|
1372,5
|
1615
|
|
1,6
|
1010,5
|
1258
|
1510,5
|
1768
|
|
1,7
|
1124,5
|
1387
|
1654,5
|
1927
|
|
1,8
|
1244,5
|
1522
|
1804,5
|
2092
|
|
1,9
|
1370,5
|
1663
|
1960,5
|
2263
|
|
2
|
1502,5
|
1810
|
2122,5
|
2440
|
|
При среднем давлении на основание 0,1 МПа
для плиты из бетона М 300
|
|
0,4
|
139,3
|
222,8
|
311,3
|
404,8
|
|
0,5
|
192,5
|
295
|
402,5
|
515
|
|
0,6
|
253,3
|
374,8
|
501,3
|
632,8
|
|
0,7
|
321,7
|
462,2
|
607,7
|
758,2
|
|
0,8
|
397,7
|
557,2
|
721,7
|
891,2
|
|
0,9
|
481,3
|
659,8
|
843,3
|
1031,8
|
|
1
|
572,5
|
770
|
972,5
|
1180
|
|
1,1
|
671,3
|
887,8
|
1109,3
|
1335,8
|
|
1,2
|
777,7
|
1013,2
|
1253,7
|
1499,2
|
|
1,3
|
891,7
|
1146,2
|
1405,7
|
1670,2
|
|
1,4
|
1013,3
|
1286,8
|
1565,3
|
1848,8
|
|
1,5
|
1142,5
|
1435
|
1732,5
|
2035
|
|
1,6
|
1279,3
|
1590,8
|
1907,3
|
2228,8
|
|
1,7
|
1423,7
|
1754,2
|
2089,7
|
2430,2
|
|
1,8
|
1575,7
|
1925,2
|
2279,7
|
2639,2
|
|
1,9
|
1735,3
|
2103,8
|
2477,3
|
2855,8
|
|
2
|
1902,5
|
2290
|
2682,5
|
3080
|
|
При среднем давлении на основание 0,2 МПа
для плиты из бетона М 200
|
|
0,4
|
127,4
|
210,4
|
303,4
|
406,4
|
|
0,5
|
175
|
275
|
385
|
505
|
|
0,6
|
229,4
|
346,4
|
473,4
|
610,4
|
|
0,7
|
290,6
|
424,6
|
568,6
|
722,6
|
|
0,8
|
358,6
|
509,6
|
670,6
|
841,6
|
|
0,9
|
433,4
|
601,4
|
779,4
|
967,4
|
|
1
|
515
|
700
|
895
|
1100
|
|
1,1
|
603,4
|
805,4
|
1017,4
|
1239,4
|
|
1,2
|
698,6
|
917,6
|
1146,6
|
1385,6
|
|
1,3
|
800,6
|
1036,6
|
1282,6
|
1538,6
|
|
1,4
|
909,4
|
1162,4
|
1425,4
|
1698,4
|
|
1,5
|
1025
|
1295
|
1575
|
1865
|
|
1,6
|
1147,4
|
1434,4
|
1731,4
|
2038,4
|
|
1,7
|
1276,6
|
1580,6
|
1894,6
|
2216,6
|
|
1,8
|
1412,6
|
1733,6
|
2064,6
|
2405,6
|
|
1,9
|
1555,4
|
1893,4
|
2241,4
|
2599,4
|
|
2
|
1705
|
2060
|
2425
|
2800
|
|
При среднем
давлении на основание 0,2 МПа для плиты из бетона М 300
|
|
0,4
|
156,2
|
255,2
|
364,2
|
483,2
|
|
0,5
|
215
|
335
|
465
|
605
|
|
0,6
|
282,2
|
423,2
|
574,2
|
735,2
|
|
0,7
|
357,8
|
519,8
|
691,8
|
873,8
|
|
0,8
|
441,8
|
624,8
|
817,8
|
1020,8
|
|
0,9
|
534,2
|
738,2
|
952,2
|
1176,2
|
|
1
|
635
|
860
|
1095
|
1340
|
|
1,1
|
744,2
|
990,2
|
1246,2
|
1512,2
|
|
1,2
|
861,8
|
1128,8
|
1405,8
|
1692,8
|
|
1,3
|
987,8
|
1275,8
|
1573,8
|
1881,8
|
|
1,4
|
1122,2
|
1431,2
|
1750,2
|
2079,2
|
|
1,5
|
1265
|
1595
|
1935
|
2285
|
|
1,6
|
1416,2
|
1767,2
|
2128,2
|
2499,2
|
|
1,7
|
1575,8
|
1947,8
|
2329,8
|
2721,8
|
|
1,8
|
1743,8
|
2136,8
|
2539,8
|
2952,8
|
|
1,9
|
1920,2
|
2334,2
|
2758,2
|
3192,2
|
|
2
|
2105
|
2540
|
2985
|
3440
|
|
При среднем давлении на основание 0,3 МПа
для плиты из бетона М200
|
|
0,4
|
144,3
|
242,8
|
356,3
|
484,8
|
|
0,5
|
197,5
|
315
|
447,5
|
595
|
|
0,6
|
258,3
|
394,8
|
546,3
|
712,8
|
|
0,7
|
326,7
|
482,2
|
652,7
|
838,2
|
|
0,8
|
402,7
|
577,2
|
766,7
|
971,2
|
|
0,9
|
486,3
|
679,8
|
888,3
|
1111,8
|
|
1
|
577,5
|
790
|
1017,5
|
1260
|
|
1,1
|
676,3
|
907,8
|
1154,3
|
1415,8
|
|
1,2
|
782,7
|
1033,2
|
1298,7
|
1579,2
|
|
1,3
|
896,7
|
1166,2
|
1450,7
|
1750,2
|
|
1,4
|
1018,3
|
1306,8
|
1610,3
|
1928,8
|
|
1,5
|
1147,5
|
1455
|
1777,5
|
2115
|
|
1,6
|
1284,3
|
1610,8
|
1952,3
|
2308,8
|
|
1,7
|
1428,7
|
1774,2
|
2134,7
|
2510,2
|
|
1,8
|
1580,7
|
1945,2
|
2324,7
|
2719,2
|
|
1,9
|
1740,3
|
2123,8
|
2522,3
|
2935,8
|
|
2
|
1907,5
|
2310
|
2727,5
|
3160
|
|
При среднем давлении на основание 0,3 МПа
для плиты из бетона М 300
|
|
0,4,
|
1 173,1
|
1 287,6
|
I 417,1
|
561,6
|
|
0,5
|
237,5
|
375
|
527,5
|
695
|
|
0,6
|
311,1
|
471,6
|
647,1
|
837,6
|
|
0,7
|
393,9
|
577,4
|
775,9
|
989,4
|
|
0,8
|
485,9
|
692,4
|
913,9
|
1150,4
|
|
0,9
|
587,1
|
816,6
|
1061,1
|
1320,6
|
|
1
|
697,5
|
950
|
1217,5
|
1500
|
|
1,1
|
817,1
|
1092,6
|
1383,1 •
|
1688,6
|
|
1,2
|
945,9
|
1244,4
|
1557,9
|
1886,4
|
|
1,3
|
1083,9
|
1405,4
|
1741,9
|
2093,4
|
|
1,4
|
1231,1
|
1575,6
|
1935,1
|
2309,6
|
|
1,5
|
1387,5
|
1755
|
2137,5
|
2535
|
|
1,6
|
1553,1
|
1943,6
|
2349,1
|
2769,6
|
|
1,7
|
1727,9
|
2141,4
|
2569,9
|
3013,4
|
|
1,8
|
1911,9
|
2348,4
|
2799,9
|
3266,4
|
|
1,9
|
2105,1
|
2564,6
|
3039,1
|
3528,6
|
|
2
|
2307,5
|
2790
|
3287,5
|
3800
|
|
При среднем давлении на основание 0,4 МПа
для плиты из бетона М200
|
|
0,4
|
161,2
|
275,2
|
409,2
|
563,2
|
|
0,5
|
220
|
355
|
510
|
685
|
|
0,6
|
287,2
|
443,2
|
619,2
|
815,2
|
|
0,7
|
362,8
|
539,8
|
736,8
|
953,8
|
|
0,8
|
446,8
|
644,8
|
862,8
|
1100,8
|
|
0,9
|
539,2
|
758,2
|
997,2
|
1256,2
|
|
1
|
640
|
880
|
1140
|
1420
|
|
1,1
|
749,2
|
1010,2
|
1291,2
|
1592,2
|
|
1,2
|
866,8
|
1148,8
|
1450,8
|
1772,8
|
|
1,3
|
992,8
|
1295,8
|
1618,8
|
1961,8
|
|
1,4
|
1127,2
|
1451,2
|
1795,2
|
2159,2
|
|
1,5
|
1270
|
1615
|
1980
|
2365
|
|
1,6
|
1421,2
|
1787,2
|
2173,2
|
2579,2
|
|
1,7
|
1580,8
|
1967,8
|
2374,8
|
2801,8
|
|
1,8
|
1748,8
|
2156,8
|
2584,8
|
3032,8
|
|
1,9
|
1925,2
|
2354,2
|
2803,2
|
3272,2
|
|
2
|
2110
|
2560
|
3030
|
3520
|
|
При среднем давлении на основание 0,4 MПа для плиты из бетона М 300
|
|
0,4
|
190
|
320
|
470
|
640
|
|
0,5
|
260
|
415
|
590
|
785
|
|
0,6,
|
340
|
520
|
720
|
940
|
|
0,7
|
430
|
635
|
860
|
1105
|
|
0,8
|
530
|
760
|
1010
|
1280
|
|
0,9
|
640
|
895
|
1170
|
1465
|
|
1
|
760
|
1040
|
1340
|
1660
|
|
1,1
|
890
|
1195
|
1520
|
1865
|
|
1,2
|
1030
|
1360
|
1710
|
2080
|
|
1,3
|
1180
|
1535
|
1910
|
2305
|
|
1,4
|
1340
|
1720
|
2120
|
2540
|
|
1,5
|
1510
|
1915
|
2340
|
2785
|
|
1,6
|
1690
|
2120
|
2570
|
3040
|
|
1,7
|
1880
|
2335
|
2810
|
3305
|
|
1,8
|
2080
|
2560
|
3060
|
3580
|
|
1,9
|
2290
|
2795
|
3320
|
3865
|
|
2
|
2510
|
3040
|
3590
|
4160
|
3.10. Осадки Sn точек n фундамента (рис. 6) определяют по следующей формуле, если в соответствии
с указаниями п. 3.4 требуется проверка разностей осадок участков фундамента,
где
 - безразмерная расчетная величина,
определяемая по табл. 12 - 21 в
зависимости от вычисляемых по формулам табл.
22 приведенных (в долях от L) расстояния δkij нагрузки Рij от ближайшего
края фундамента и величин ξ, η найденных по координатам точки ij (xij, yij) приложения нагрузки Рij и рассматриваемой точки n (хn, уn) фундамента
в системе координат, начало которой - безразмерная расчетная величина,
определяемая по табл. 12 - 21 в
зависимости от вычисляемых по формулам табл.
22 приведенных (в долях от L) расстояния δkij нагрузки Рij от ближайшего
края фундамента и величин ξ, η найденных по координатам точки ij (xij, yij) приложения нагрузки Рij и рассматриваемой точки n (хn, уn) фундамента
в системе координат, начало которой
Таблица 12
Осадки 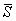
δ = 0
|
η
|
ξ
|
|
0,0
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
3,2
|
3,6
|
4,0
|
|
0,0
|
0,66
|
0,57
|
0,49
|
0,42
|
0,36
|
0,30
|
0,27
|
0,20
|
0,16
|
0,15
|
0,13
|
0,12
|
0,10
|
0,09
|
|
0,2
|
0,64
|
0,55
|
0,48
|
0,41
|
0,35
|
0,30
|
0,26
|
0,20
|
0,16
|
0,14
|
0,13
|
0,12
|
0,10
|
0,09
|
|
0,4
|
0,59
|
0,52
|
0,45
|
0,39
|
0,34
|
0,29
|
0,25
|
0,19
|
0,16
|
0,14
|
0,12
|
0,12
|
0,10
|
0,09
|
|
0,6
|
0,53
|
0,47
|
0,41
|
0,36
|
0,31
|
0,27
|
0,24
|
0,18
|
0,15
|
0,13
|
0,12
|
0,12
|
0,10
|
0,09
|
|
0,8
|
0,47
|
0,41
|
0,37
|
0,32
|
0,28
|
0,25
|
0,22
|
0,17
|
0,14
|
0,12
|
0,12
|
0,11
|
0,09
|
0,09
|
|
1,0
|
0,40
|
0,36
|
0,32
|
0,29
|
0,25
|
0,22
|
0,20
|
0,16
|
0,13
|
0,12
|
0,11
|
0,10
|
0,09
|
0,09
|
|
1,2
|
0,33
|
0,31
|
0,28
|
0,25
|
0,22
|
0,20
|
0,17
|
0,14
|
0,11
|
0,10
|
0,11
|
0,10
|
0,09
|
0,08
|
|
1,6
|
0,22
|
0,20
|
0,19
|
0,18
|
0,16
|
0,14
|
0,13
|
0,11
|
0,10
|
0,11
|
0,10
|
0,09
|
0,08
|
0,07
|
|
2,0
|
0,14
|
0,13
|
0,13
|
0,12
|
0,11
|
0,10
|
0,10
|
0,10
|
0,08
|
0,09
|
0,08
|
0,08
|
0,08
|
0,07
|
Таблица
13
Осадки 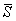
δ = 0,1
|
η
|
ξ
|
|
0,0
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
3,2
|
3,6
|
4,0
|
|
0,0
|
0,61
|
0,54
|
0,48
|
0,42
|
0,36
|
0,31
|
0,28
|
0,22
|
0,18
|
0,16
|
0,14
|
0,12
|
0,10
|
0,09
|
|
0,2
|
0,59
|
0,53
|
0,47
|
0,41
|
0,35
|
0,30
|
0,28
|
0,22
|
0,18
|
0,16
|
0,14
|
0,12
|
0,10
|
0,09
|
|
0,4
|
0,56
|
0,51
|
0,46
|
0,40
|
0,35
|
0,30
|
0,27
|
0,21
|
0,18
|
0,15
|
0,13
|
0,12
|
0,10
|
0,00
|
|
0,6
|
0,50
|
0,48
|
0,43
|
0,39
|
0,34
|
0,30
|
0,26
|
0,20
|
0,17
|
0,15
|
0,12
|
0,12
|
0,10
|
0,09
|
|
0,8
|
0,44
|
0,41
|
0,39
|
0,34
|
0,30
|
0,27
|
0,24
|
0,19
|
0,16
|
0,14
|
0,12
|
0,11
|
0,09
|
0,0
|
|
1,0
|
0,38
|
0,37
|
0,34
|
0,32
|
0,28
|
0,25
|
0,22
|
0,18
|
0,15
|
0,13
|
0,11
|
0,11
|
0,09
|
0,08
|
|
1,2
|
0,32
|
0,31
|
0,30
|
0,28
|
0,25
|
0,22
|
0,19
|
0,16
|
0,13
|
0,12
|
0,11
|
0,10
|
0,09
|
0,08
|
|
1,6
|
0,21
|
0,22
|
0,21
|
0,20
|
0,19
|
0,17
|
0,15
|
0,14
|
0,12
|
0,14
|
0,10
|
0,10
|
0,08
|
0,07
|
|
2,0
|
0,14
|
0,15
|
0,15
|
0,14
|
0,13
|
0,12
|
0,12
|
0,12
|
0,11
|
0,10
|
0,09
|
0,09
|
0,08
|
0,07
|
Таблица
14
Осадки 
δ = 0,2
|
η
|
ξ
|
|
0,0
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
3,2
|
3,6
|
4,0
|
|
0,0
|
0,57
|
0,52
|
0,48
|
0,43
|
0,37
|
0,32
|
0,30
|
0,24
|
0,20
|
0,17
|
0,15
|
0,12
|
0,11
|
0,09
|
|
0,2
|
0,55
|
0,51
|
0,47
|
0,42
|
0,36
|
0,32
|
0,30
|
0,24
|
0,20
|
0,17
|
0,15
|
0,12
|
0,11
|
0,09
|
|
0,4
|
0,52
|
0,50
|
0,46
|
0,41
|
0,36
|
0,31
|
0,28
|
0,22
|
0,19
|
0,16
|
0,13
|
0,12
|
0,11
|
0,09
|
|
0,6
|
0,47
|
0,48
|
0,44
|
0,40
|
0,35
|
0,30
|
0,27
|
0,21
|
0,18
|
0,16
|
0,13
|
0,11
|
0,10
|
0,08
|
|
0,8
|
0,41
|
0,41
|
0,40
|
0,36
|
0,32
|
0,29
|
0,25
|
0,20
|
0,17
|
0,15
|
0,12
|
0,11
|
0,10
|
0,08
|
|
1,0
|
0,36
|
0,37
|
0,35
|
0,38
|
0,30
|
0,27
|
0,23
|
0,19
|
0,16
|
0,14
|
0,12
|
0,11
|
0,10
|
0,08
|
|
1,2
|
0,30
|
0,32
|
0,31
|
0,30
|
0,27
|
0,24
|
0,21
|
0,18
|
0,15
|
0,14
|
0,12
|
0,10
|
0,09
|
0,08
|
|
1,6
|
0,21
|
0,23
|
0,22
|
0,22
|
0,21
|
0,19
|
0,17
|
0,16
|
0,14
|
0,13
|
0,12
|
0,10
|
0,09
|
0,08
|
|
2,0
|
0,14
|
0,15
|
0,15
|
0,15
|
0,14
|
0,14
|
0,14
|
0,14
|
0,13
|
0,12
|
0,11
|
0,10
|
0,09
|
0,08
|
Таблица
15
Осадки 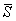
δ = 0,4
|
η
|
ξ
|
|
0,0
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
3,2
|
3,6
|
4,0
|
|
0,0
|
0,49
|
0,48
|
0,48
|
0,46
|
0,42
|
0,38
|
0,35
|
0,29
|
0,24
|
0,20
|
0,17
|
0,14
|
0,12
|
0,10
|
|
0,2
|
0,47
|
0,47
|
0,47
|
0,44
|
0,41
|
0,38
|
0,35
|
0,29
|
0,24
|
0,20
|
0,17
|
0,14
|
0,12
|
0,10
|
|
0,4
|
0,45
|
0,46
|
0,45
|
0,43
|
0,40
|
0,37
|
0,34
|
0,29
|
0,24
|
0,19
|
0,16
|
0,14
|
0,12
|
0,10
|
|
0,6
|
0,41
|
0,44
|
0,42
|
0,40
|
0,39
|
0,36
|
0,34
|
0,28
|
0,23
|
0,18
|
0,15
|
0,13
|
0,11
|
0,10
|
|
0,8
|
0,36
|
0,40
|
0,39
|
0,37
|
0,36
|
0,35
|
0,33
|
0,26
|
0,22
|
0,18
|
0,15
|
0,13
|
0,11
|
0,10
|
|
1,0
|
0,32
|
0,35
|
0,36
|
0,33
|
0,32
|
0,30
|
0,30
|
0,24
|
0,21
|
0,17
|
0,14
|
0,12
|
0,11
|
0,10
|
|
1,2
|
0,28
|
0,31
|
0,32
|
0,30
|
0,28
|
0,27
|
0,27
|
0,22
|
0,20
|
0,16
|
0,14
|
0,12
|
0,11
|
0,09
|
|
1,6
|
0,19
|
0,23
|
0,23
|
0,22
|
0,22
|
0,22
|
0,21
|
0,19
|
0,18
|
0,15
|
0,13
|
0,11
|
0,10
|
0,09
|
|
2,0
|
0,13
|
0,17
|
0,18
|
0,18
|
0,18
|
0,18
|
0,18
|
0,17
|
0,16
|
0,14
|
0,12
|
0,11
|
0,09
|
0,09
|
Таблица 16
Осадки 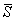
δ = 0,6
|
η
|
ξ
|
|
0,0
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
3,2
|
3,6
|
4,0
|
|
0,0
|
0,42
|
0,43
|
0,46
|
0,48
|
0,46
|
0,43
|
0,39
|
0,33
|
0,27
|
0,23
|
0,19
|
0,16
|
0,13
|
0,11
|
|
0,2
|
0,41
|
0,42
|
0,44
|
0,47
|
0,45
|
0,42
|
0,39
|
0,33
|
0,27
|
0,23
|
0,19
|
0,16
|
0,13
|
0,11
|
|
0,4
|
0,39
|
0,41
|
0,43
|
0,44
|
0,42
|
0,39
|
0,37
|
0,32
|
0,26
|
0,22
|
0,18
|
0,15
|
0,13
|
0,11
|
|
0,6
|
0,36
|
0,41
|
0,40
|
0,40
|
0,38
|
0,36
|
0,35
|
0,31
|
0,26
|
0,21
|
0,17
|
0,14
|
0,12
|
0,10
|
|
0,8
|
0,32
|
0,36
|
0,37
|
0,35
|
0,33
|
0,32
|
0,32
|
0,30
|
0,25
|
0,20
|
0,16
|
0,13
|
0,11
|
0,10
|
|
1,0
|
0,29
|
0,33
|
0,33
|
0,30
|
0,29
|
0,29
|
0,28
|
0,27
|
0,24
|
0,19
|
0,15
|
0,12
|
0,11
|
0,10
|
|
1,2
|
0,25
|
0,30
|
0,30
|
0,28
|
0,27
|
0,27
|
0,24
|
0,25
|
0,22
|
0,17
|
0,13
|
0,12
|
0,11
|
0,10
|
|
1,6
|
0,18
|
0,21
|
0,22
|
0,23
|
0,23
|
0,23
|
0,22
|
0,21
|
0,19
|
0,16
|
0,12
|
0,12
|
0,11
|
0,09
|
|
2,0
|
0,12
|
0,15
|
0,18
|
0,20
|
0,19
|
0,19
|
0,18
|
0,17
|
0,16
|
0,15
|
0,12
|
0,11
|
0,10
|
0,09
|
Таблица 17
Осадки 
δ = 0,8
|
η
|
ξ
|
|
0,0
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
3,2
|
3,6
|
4,0
|
|
0,0
|
0,36
|
0,37
|
0,42
|
0,46
|
0,47
|
0,45
|
0,41
|
0,35
|
0,29
|
0,25
|
0,20
|
0,16
|
0,13
|
0,11
|
|
0,2
|
0,35
|
0,36
|
0,41
|
0,45
|
0,46
|
0,44
|
0,41
|
0,35
|
0,29
|
0,25
|
0,20
|
0,16
|
0,13
|
0,11
|
|
0,4
|
0,34
|
0,36
|
0,40
|
0,42
|
0,44
|
0,42
|
0,40
|
0,34
|
0,29
|
0,24
|
0,20
|
0,16
|
0,13
|
0,11
|
|
0,6
|
0,31
|
0,35
|
0,39
|
0,38
|
0,39
|
0,38
|
0,37
|
0,32
|
0,28
|
0,23
|
0,19
|
0,15
|
0,13
|
0,11
|
|
0,8
|
0,28
|
0,32
|
0,36
|
0,33
|
0,35
|
0,34
|
0,33
|
0,31
|
0,27
|
0,22
|
0,18
|
0,15
|
0,13
|
0,11
|
|
1,0
|
0,25
|
0,30
|
0,32
|
0,29
|
0,31
|
0,30
|
0,30
|
0,28
|
0,25
|
0,21
|
0,17
|
0,15
|
0,12
|
0,11
|
|
1,2
|
0,22
|
0,27
|
0,28
|
0,27
|
0,29
|
0,28
|
0,28
|
0,26
|
0,24
|
0,20
|
0,16
|
0,14
|
0,12
|
0,10
|
|
1,6
|
0,16
|
0,21
|
0,22
|
0,23
|
0,24
|
0,23
|
0,23
|
0,23
|
0,21
|
0,17
|
0,15
|
0,13
|
0,11
|
0,10
|
|
2,0
|
0,11
|
0,14
|
0,18
|
0,19
|
0,20
|
0,20
|
0,20
|
0,19
|
0,17
|
0,15
|
0,13
|
0,12
|
0,11
|
0,09
|
принято в левом верхнем углу
фундамента;
ось х направлена вдоль длинной
стороны вправо, ось у - вдоль короткой стороны вниз по
плану фундамента;
Eпрср - осредненный
приведенный модуль деформации основания, определяемый по указаниям разд. 2;
mЕ -
корректирующий коэффициент, вычисляемый по п. 3.11;
μср - осредненный
коэффициент бокового расширения грунта основания, определяемый по рекомендациям
разд.
2;
L - упругая
характеристика плитного фундамента, вычисляемая по формуле
здесь
h -
толщина фундамента;
Еb - начальный модуль упругости
бетона;
μб - коэффициент Пуассона
бетона;
Рi,j - вертикальная нагрузка на колонну.
Таблица 18
Осадки 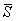
δ = 1,2
|
η
|
ξ
|
|
0,0
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
3,2
|
3,6
|
4,0
|
|
0,0
|
0,28
|
0,30
|
0,35
|
0,39
|
0,41
|
0,42
|
0,43
|
0,40
|
0,34
|
0,29
|
0,23
|
0,19
|
0,16
|
0,13
|
|
0,2
|
0,28
|
0,30
|
0,35
|
0,39
|
0,41
|
0,42
|
0,42
|
0,39
|
0,34
|
0,29
|
0,23
|
0,19
|
0,16
|
0,13
|
|
0,4
|
0,27
|
0,28
|
0,34
|
0,37
|
0,40
|
0,40
|
0,40
|
0,38
|
0,33
|
0,28
|
0,23
|
0,18
|
0,16
|
0,13
|
|
0,6
|
0,26
|
0,27
|
0,34
|
0,35
|
0,37
|
0,38
|
0,38
|
0,38
|
0,32
|
0,27
|
0,22
|
0,18
|
0,16
|
0,13
|
|
0,8
|
0,24
|
0,25
|
0,33
|
0,32
|
0,33
|
0,36
|
0,.36
|
0,34
|
0,30
|
0,26
|
0,21
|
0,17
|
0,16
|
0,13
|
|
1,0
|
0,22
|
0,23
|
0,30
|
0,28
|
0,30
|
0,32
|
0,33
|
0,31
|
0,28
|
0,24
|
0,20
|
0,17
|
0,15
|
0,12
|
|
1,2
|
0,19
|
0,21
|
0,27
|
0,26
|
0,28
|
0,29
|
0,30
|
0,29
|
0,27
|
0,22
|
0,19
|
0,17
|
0,14
|
0,12
|
|
1,6
|
0,15
|
0,17
|
0,21
|
0,22
|
0,23
|
0,24
|
0,24
|
0,24
|
0,21
|
0,19
|
0,17
|
0,15
|
0,13
|
0,12
|
|
2,0
|
0,12
|
0,14
|
0,18
|
0,18
|
0,20
|
0,20
|
0,20
|
0,20
|
0,18
|
0,17
|
0,15
|
,013
|
0,12
|
0,11
|
Таблица 19
Осадки 
δ = 1,6
|
η
|
ξ
|
|
0,0
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
3,2
|
3,6
|
4,0
|
|
0,0
|
0,20
|
0,24
|
0,29
|
0,33
|
0,35
|
0,37
|
0,40
|
0,42
|
0,38
|
0,35
|
0,31
|
0,27
|
0,23
|
0,18
|
|
0,2
|
0,19
|
0,23
|
0,29
|
0,32
|
0,35
|
0,37
|
0,39
|
0,42
|
0,38
|
0,35
|
0,31
|
0,27
|
0,23
|
0,18
|
|
0,4
|
0,19
|
0,22
|
0,29
|
0,31
|
0,34
|
0,36
|
0,38
|
0,40
|
0,37
|
0,35
|
0,31
|
0,27
|
0,23
|
0,18
|
|
0,6
|
0,18
|
0,21
|
0,28
|
0,30
|
0,32
|
0,34
|
0,36
|
0,38
|
0,35
|
0,33
|
0,30
|
0,26
|
0,22
|
0,17
|
|
0,8
|
0,17
|
0,20
|
0,24
|
0,29
|
0,31
|
0,32
|
0,34
|
0,35
|
0,33
|
0,32
|
0,28
|
0,25
|
0,22
|
0,17
|
|
1,0
|
0,16
|
0,19
|
0,24
|
0,27
|
0,28
|
0,30
|
0,31
|
0,32
|
0,30
|
0,30
|
0,27
|
0,23
|
0,20
|
0,16
|
|
1,2
|
0,14
|
0,18
|
0,22
|
0,25
|
0,26
|
0,28
|
0,29
|
0,30
|
0,29
|
0,28
|
0,25
|
0,22
|
0,29
|
0,15
|
|
1,6
|
0,11
|
0,16
|
0,19
|
0,21
|
0,23
|
0,23
|
0,24
|
0,25
|
0,24
|
0,23
|
0,21
|
0,18
|
0,16
|
0,13
|
|
2,0
|
0,10
|
0,14
|
0,16
|
0,17
|
0,19
|
0,19
|
0,20
|
0,20
|
0,19
|
0,19
|
0,16
|
0,14
|
0,13
|
0,12
|
Таблица 20
Осадки 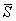
δ = 2,0
|
η
|
ξ
|
|
0,0
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
3,2
|
3,6
|
4,0
|
|
0,0
|
0,16
|
0,20
|
0,24
|
0,27
|
0,29
|
0,32
|
0,34
|
0,38
|
0,41
|
0,38
|
0,34
|
0,29
|
0,24
|
0,20
|
|
0,2
|
0,16
|
0,20
|
0,24
|
0,27
|
0,29
|
0,31
|
0,34
|
0,38
|
0,41
|
0,38
|
0,34
|
0,29
|
0,24
|
0,20
|
|
0,4
|
0,16
|
0,20
|
0,24
|
0,26
|
0,29
|
0,31
|
0,32
|
0,37
|
0,38
|
0,37
|
0,33
|
0,29
|
0,24
|
0,20
|
|
0,6
|
0,15
|
0,18
|
0,24
|
0,26
|
0,28
|
0,30
|
0,31
|
0,35
|
0,36
|
0,34
|
0,31
|
0,28
|
0,24
|
0,19
|
|
0,8
|
0,14
|
0,17
|
0,23
|
0,25
|
0,27
|
0,28
|
0,30
|
0,33
|
0,34
|
0,33
|
0,30
|
0,26
|
0,23
|
0,19
|
|
1,0
|
0,13
|
0,16
|
0,22
|
0,24
|
0,25
|
0,26
|
0,28
|
0,31
|
0,32
|
0,31
|
0,28
|
0,25
|
0,23
|
0,18
|
|
1,2
|
0,11
|
0,15
|
0,21
|
0,22
|
0,24
|
0,24
|
0,26
|
0,29
|
0,29
|
0,28
|
0,26
|
0,23
|
0,20
|
0,17
|
|
1,6
|
0,10
|
0,14
|
0,18
|
0,19
|
0,21
|
0,21
|
0,22
|
0,24
|
0,24
|
0,23
|
0,22
|
0,14
|
0,17
|
0,14
|
|
2,0
|
0,09
|
0,13
|
0,16
|
0,16
|
0,17
|
0,17
|
0,17
|
0,19
|
0,19
|
0,19
|
0,18
|
0,16
|
0,14
|
0,13
|
Таблица 21
Осадки 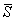
δ > 2
|
η
|
ξ
|
|
0,0
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
1,8
|
|
0,0
|
0,385
|
0,377
|
0,359
|
0,338
|
0,314
|
0,291
|
0,268
|
0,226
|
0,207
|
|
0,2
|
0,377
|
0,371
|
0,354
|
0,334
|
0,312
|
0,289
|
0,266
|
0,225
|
0,206
|
|
0,4
|
0,359
|
0,354
|
0,341
|
0,324
|
0,304
|
0,281
|
0,261
|
0,221
|
0,203
|
|
0,6
|
0,338
|
0,334
|
0,324
|
0,308
|
0,291
|
0,271
|
0,253
|
0,215
|
0,198
|
|
0,8
|
0,314
|
0,312
|
0,304
|
0,291
|
0,276
|
0,259
|
0,243
|
0,208
|
0,192
|
|
1,0
|
0,291
|
0,289
|
0,281
|
0,271
|
0,259
|
0,246
|
0,232
|
0,199
|
0,184
|
|
1,2
|
0,268
|
0,266
|
0,261
|
0,253
|
0,243
|
0,232
|
0,216
|
0,189
|
0,176
|
|
1,4
|
0,247
|
0,246
|
0,241
|
0,234
|
0,225
|
0,214
|
0,203
|
0,179
|
0,167
|
|
1,6
|
0,226
|
0,225
|
0,221
|
0,215
|
0,208
|
0,199
|
0,189
|
0,169
|
0,158
|
|
1,8
|
0,207
|
0,206
|
0,203
|
0,198
|
0,192
|
0,184
|
0,176
|
0,158
|
0,150
|
|
2,0
|
0,189
|
0,188
|
0,186
|
0,182
|
0,177
|
0,170
|
0,164
|
0,149
|
0,141
|
|
2,2
|
0,173
|
0,172
|
0,170
|
0,167
|
0,163
|
0,158
|
0,152
|
0,139
|
0,133
|
|
2,4
|
0,159
|
0,158
|
0,157
|
0,155
|
0,151
|
0,146
|
0,141
|
0,131
|
0,124
|
|
2,6
|
0,146
|
0,145
|
0,144
|
0,142
|
0,139
|
0,136
|
0,132
|
0,122
|
0,117
|
Продолжение таблицы 21
Осадки 
δ > 2
|
η
|
ξ
|
|
2,0
|
2,2
|
2,4
|
2,6
|
2,8
|
3,0
|
3,2
|
3,4
|
3,6
|
3,8
|
0,4
|
|
0,0
|
0,189
|
0,173
|
0,159
|
0,146
|
0,135
|
0,124
|
0,115
|
0,107
|
0,099
|
0,093
|
0,087
|
|
0,2
|
0,188
|
0,172
|
0,158
|
0,146
|
0,135
|
0,124
|
0,115
|
0,107
|
0,099
|
0,093
|
0,087
|
|
0,4
|
0,186
|
0,170
|
0,157
|
0,144
|
0,133
|
0,123
|
0,114
|
0,106
|
0,098
|
0,092
|
0,086
|
|
0,6
|
0,182
|
0,167
|
0,155
|
0,142
|
0,131
|
0,121
|
0,113
|
0,105
|
0,097
|
0,091
|
0,086
|
|
0,8
|
0,177
|
0,163
|
0,151
|
0,139
|
0,129
|
0,119
|
0,111
|
0,103
|
0,096
|
0,089
|
|
|
1,0
|
0,170
|
0,158
|
0,146
|
0,136
|
0,126
|
0,117
|
0,109
|
0,101
|
0,095
|
0,089
|
|
|
1,2
|
0,164
|
0,152
|
0,141
|
0,132
|
0,122
|
0,113
|
0,106
|
0,099
|
0,093
|
0,087
|
|
|
1,4
|
0,157
|
0,145
|
0,136
|
0,127
|
0,118
|
0,111
|
0,103
|
0,097
|
0,091
|
0,086
|
|
|
1,6
|
0,149
|
0,139
|
0,131
|
0,122
|
0,114
|
0,107
|
0,100
|
0,094
|
0,089
|
|
|
|
1,8
|
0,141
|
0,133
|
0,124
|
0,117
|
0,110
|
0,103
|
0,097
|
0,091
|
0,086
|
|
|
|
1,0
|
0,133
|
0,126
|
0,118
|
0,112
|
0,106
|
0,099
|
0,094
|
0,089
|
|
|
|
|
2,2
|
0,126
|
0,119
|
0,112
|
0,107
|
0,101
|
0,095
|
0,091
|
0,086
|
|
|
|
|
2,4
|
0,118
|
0,112
|
0,107
|
0,101
|
0,096
|
0,092
|
0,086
|
|
|
|
|
Продолжение таблицы 21
Осадки 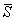
δ > 2
|
η
|
ξ
|
|
0,0
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,4
|
1,6
|
1,8
|
|
2,8
|
0,135
|
0,134
|
0,133
|
0,131
|
0,129
|
0,126
|
0,122
|
0,118
|
0,114
|
0,110
|
|
3,0
|
0,124
|
0,124
|
0,123
|
0,121
|
0,119
|
0,117
|
0,113
|
0,111
|
0,107
|
0,103
|
|
3,2
|
0,115
|
0,115
|
0,114
|
0,113
|
0,111
|
0,109
|
0,106
|
0,103
|
0,100
|
0,097
|
|
3,4
|
0,107
|
0,107
|
0,106
|
0,105
|
0,108
|
0,101
|
0,099
|
0,097
|
0,094
|
0,091
|
|
3,6
|
0,099
|
0,099
|
0,098
|
0,097
|
0,096
|
0,095
|
0,093
|
0,091
|
0,089
|
0,086
|
|
3,8
|
0,093
|
0,093
|
0,092
|
0,091
|
0,090
|
0,089
|
0,087
|
0,086
|
|
|
|
4,0
|
0,087
|
0,087
|
0,086
|
0,086
|
|
|
|
|
|
|
Продолжение
таблицы 21
Осадки 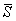
δ > 2
|
η
|
ξ
|
|
2,0
|
2,2
|
2,4
|
2,6
|
2,8
|
3,0
|
3,2
|
3,4
|
3,6
|
3,8
|
4,0
|
|
2,6
|
0,112
|
0,107
|
0,101
|
0,097
|
0,092
|
0,088
|
|
|
|
|
|
|
2,8
|
0,106
|
0,101
|
0,096
|
0,092
|
0,088
|
|
|
|
|
|
|
|
3,0
|
0,099
|
0,095
|
0,092
|
0,088
|
|
|
|
|
|
|
|
|
3,2
|
0,094
|
0,091
|
0,086
|
|
|
|
|
|
|
|
|
|
3,4
|
0,089
|
0,086
|
|
|
|
|
|
|
|
|
|
Таблица 22
|
Расстояние нагрузки
от края фундамента δki j
|
Вводы в табл. 12
- 21
|
|
ξ
|
η
|
|

|
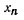
|
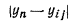
|
|
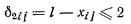
|

|
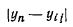
|
|
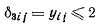
|

|
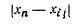
|
|

|

|

|
|

|

|

|
Вводы в табл. 12 - 21
приведены в табл. 22.
В табл.
22 l и b -
соответственно длина и ширина плитного фундамента.
Безразмерную величину 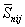 определяют по табл. 21, если все значения δkij > 2. Если величины ξ или η окажутся
больше табличных значений, то принимают определяют по табл. 21, если все значения δkij > 2. Если величины ξ или η окажутся
больше табличных значений, то принимают  . .
Из величин 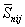 , полученных
по табл. 12 - 20, выбирают большую. , полученных
по табл. 12 - 20, выбирают большую.
3.11. Корректирующий
коэффициент mЕ находят по формуле
где
ωср - коэффициент,
определяемый по табл. 23 в зависимости от отношения длины фундамента к ширине n = l/b и толщины сжимаемого слоя Н
либо Нэ к полуширине фундамента m' = 2Н/b либо m' = 2Нa/b. Величины Н
и Нa находят по указаниям разд. 2
с учетом принятой расчетной схемы для расчета деформаций основания;
 - коэффициент, определяемый по табл. 23 для m' = ∞ в зависимости от
отношения сторон фундамента n = l/b. - коэффициент, определяемый по табл. 23 для m' = ∞ в зависимости от
отношения сторон фундамента n = l/b.
Таблица
23
|
m' = 2Н/b
|
Значение ωср при n, равном
|
|
1
|
2
|
3
|
≥ 10
|
|
0
|
0
|
0
|
0
|
0
|
|
0,25
|
0,12
|
0,12
|
0,13
|
0,13
|
|
0,5
|
0,22
|
0,24
|
0,24
|
0,25
|
|
0,75
|
0,31
|
0,34
|
0,34
|
0,35
|
|
1
|
0,39
|
0,43
|
0,44
|
0,46
|
|
1,5
|
0,53
|
0,59
|
0,61
|
0,63
|
|
2
|
0,62
|
0,7
|
0,73
|
0,77
|
|
2,5
|
0,68
|
0,79
|
0,83
|
0,8
|
|
3
|
0,72
|
0,87
|
0,92
|
1
|
|
4
|
0,77
|
0,96
|
1,04
|
1,15
|
|
5
|
0,8
|
1,03
|
1,13
|
1,27
|
|
7
|
0,84
|
1,1
|
1,23
|
1,45
|
|
10
|
0,87
|
1,16
|
1,31
|
1,62
|
|
20
|
0,91
|
1,23
|
1,42
|
1,9
|
|
50
|
0,93
|
1,27
|
1,48
|
2,1
|
|
|
0,95
|
1,3
|
1,63
|
2,25
|
3.12. Вычисление
предварительных размеров плитного фундамента под сетку колонн выполняют по
указаниям пп.
3.3 - 3.6
следующим образом:
принимают толщину hп подколенника
в интервале от нулевого значения до заданной максимальной величины hп max с шагом 150 мм;
для принятой толщины
подколенника hп и заданных сторон колонн ak и b' определяют
по следующим формулам стороны а и b прямоугольном в плане подколенника, кратные 100 мм и
не превышающие заданные предельные величины amax и b'max :
|
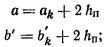
|
(39)
|
находят в соответствии с указаниями п.
3.9 толщину фундамента, требующуюся по расчету его прочности на
продавливание подколенниками при всех возможных схемах продавливания. При этом
толщина фундамента должна быть кратной 50 мм и быть не менее 300 мм;
определяют объем фундамента, ограниченный
осями крайних рядов колони, и суммируют его с объемом подколонников;
находят толщину фундамента и размеры
подколенников, при которых получен минимальный объем бетона, приходящегося на
фундамент и подколонники;
определяют длины консольных
участков фундамента lR по выбранным толщине фундамента h, сторонам а и b' подколонников, используя формулы (36) и (38). Из найденных
величин lk выбирают большую для
соответствующего ряда колонн. Если по конструктивным или иным ограничениям
нельзя принять необходимую длину консоли, а также при расчетной длине консоли,
большей 3 м, предусматривают местное утолщение плиты вдоль соответствующего
ряда колонн;
определяют осадки центров колонн по
формуле (36);
вычисляют относительные разности осадок
соседних колонн и сравнивают с предельными величинами, рекомендуемыми нормами
проектирования главы СНиП на основания зданий и сооружений. Если относительная
разность осадок соседних колонн превышает заданную предельную величину, то
увеличивают толщину фундамента и вновь отыскивают размеры подколонников, длины
консолей и относительные разности осадок соседних колонн.
3.13. В случае учета поперечной арматуры при расчете
прочности плитного фундамента на продавливание должны быть выполнены следующие
требования главы СНиП на проектирование бетонных и железобетонных конструкций:
|
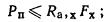
|
(40)
|
|
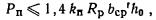
|
(41)
|
где
Fx - площадь сечения хомутов, пересекающих боковые
поверхности пирамиды продавливания;
Rа,х -
расчетное сопротивление арматуры хомутов.
Остальные обозначения те же, что и в
формуле (27).
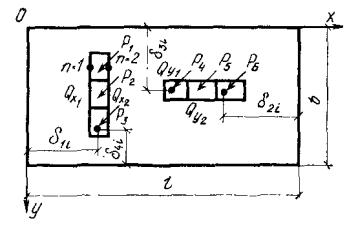
Рис. 7. Схема плитного фундамента здания с несущими
стенами
для подбора его оптимальных размеров
Pi - нагрузки на участки стен; 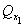 , ,  , , 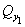 , , 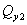 - поперечные
силы в плите; x, y – система координат - поперечные
силы в плите; x, y – система координат
3.14. Условия
прочности наклонных сечений плитного фундамента здания или сооружения с
несущими стенами на действие поперечных сил (без учета поперечного армирования)
принимают в соответствии с указаниями главы СНиП на проектирование бетонных и
железобетонных конструкций в виде зависимости
где
Q - поперечная
сила в плитном фундаменте у грани стены, приходящейся на 1 м ширины сечения
фундамента;
остальные обозначения те же, что и в
формуле (27).
3.15. Для определения поперечных сил и осадок плитного
фундамента здания или сооружения с несущими стенами следует предварительно
разбить нагруженные площадки под стенами на участки шириной, равной ширине
стены, длиной 1 - 2 м и приложить равнодействующую нагрузку Рi, в центрах i этих участков (рис. 7).
Поперечные силы 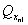 и и  находят от расчетной нагрузки,
передаваемой на фундамент стенами, расположенными параллельно оси у
(рис. 7), в сечениях фундамента, совпадающих соответственно с левыми и
правыми (по плану) границами n-го
загруженного участка. При расположении несущих стен параллельно оси х определяют поперечные силы находят от расчетной нагрузки,
передаваемой на фундамент стенами, расположенными параллельно оси у
(рис. 7), в сечениях фундамента, совпадающих соответственно с левыми и
правыми (по плану) границами n-го
загруженного участка. При расположении несущих стен параллельно оси х определяют поперечные силы 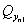 и и  вдоль границ n-го нагруженного участка, параллельных оси х,
причем поперечную силу вдоль границ n-го нагруженного участка, параллельных оси х,
причем поперечную силу  находят в сечении, которое ближе
расположено к оси х. Поперечную силу, приходящуюся на 1
м сечения фундамента, совпадающего с внешней границей n-го нагруженного участка, находят для точки n, задаваемой в середине этой
границы, как сумму поперечных сил от всех приложенных к фундаменту нагрузок Рi. находят в сечении, которое ближе
расположено к оси х. Поперечную силу, приходящуюся на 1
м сечения фундамента, совпадающего с внешней границей n-го нагруженного участка, находят для точки n, задаваемой в середине этой
границы, как сумму поперечных сил от всех приложенных к фундаменту нагрузок Рi.
3.16. Поперечные силы Qn в точках n от нагрузок Рi вычисляют по следующей формуле:
|

|
(43)
|
где
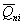 - безразмерная расчетная величина, определяемая по табл. 24 - 42 в зависимости от вычисленных по формулам
табл. 43 приведенных (в долях от L) расстояния δki нагрузки
Рi от ближайшего края
фундамента и величин ξ, η, найденных по координатам точки i (xi yi) приложения нагрузки Рi и рассматриваемой точки n (хп, уп)
фундамента в системе координат,
показанной на рис. 7; - безразмерная расчетная величина, определяемая по табл. 24 - 42 в зависимости от вычисленных по формулам
табл. 43 приведенных (в долях от L) расстояния δki нагрузки
Рi от ближайшего края
фундамента и величин ξ, η, найденных по координатам точки i (xi yi) приложения нагрузки Рi и рассматриваемой точки n (хп, уп)
фундамента в системе координат,
показанной на рис. 7;
L - упругая характеристика
плитного фундамента, вычисляемая по формуле (37);
Рi - нагрузка на фундамент, приложенная в центре i загруженного участка.
Таблица 24
Поперечные
силы 
δ = 0
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
|
0,0
|
0,24-∞
|
-2,91
|
-1,30
|
-0,50
|
-0,24
|
-0,12
|
-0,06
|
-0,02
|
0,00
|
|
0,2
|
0,21
|
-0,38
|
-0,52
|
-0,35
|
-0,19
|
-0,10
|
-0,05
|
-0,02
|
0,00
|
|
0,4
|
0,18
|
0,06
|
-0,07
|
-0,13
|
-0,10
|
-0,06
|
-0,03
|
-0,01
|
0,00
|
|
0,6
|
0,10
|
0,09
|
0,05
|
-0,01
|
-0,02
|
-0,02
|
-0,01
|
0,00
|
0,00
|
|
0,8
|
0,06
|
0,06
|
0,06
|
0,03
|
-0,02
|
0,01
|
-0,01
|
0,01
|
0,00
|
|
1,0
|
-0,01
|
0,02
|
0,03
|
0,03
|
0,03
|
0,02
|
0,01
|
0,01
|
0,00
|
|
1,2
|
-0,08
|
-0,04
|
-0,01
|
0,01
|
0,02
|
0,02
|
0,01
|
0,01
|
0,00
|
|
1,6
|
-0,12
|
-0,11
|
-0,08
|
-0,03
|
-0,01
|
0,00
|
0,00
|
0,00
|
0,00
|
Таблица 25
Поперечные
силы 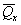
δ = 0,1
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
|
0,0
|
0,22
|
±∞
|
-1,69
|
-0,54
|
-0,27
|
-0,14
|
-0,07
|
-0,14
|
0,03
|
|
0,2
|
0,19
|
-0,14
|
-0,40
|
-0,37
|
-0,22
|
-0,12
|
-0,06
|
-0,14
|
0,03
|
|
0,4
|
0,15
|
-0,05
|
-0,13
|
-0,16
|
-0,13
|
-0,07
|
-0,03
|
-0,00
|
0,04
|
|
0,6
|
0,08
|
0,01
|
-,0,02
|
-0,04
|
-0,04
|
-0,02
|
0,00
|
0,03
|
0,04
|
|
0,8
|
0,01
|
0,04
|
0,06
|
0,04
|
0,03
|
0,03
|
0,03
|
0,05
|
0,06
|
|
1,0
|
-0,04
|
0,08
|
0,11
|
0,08
|
0,07
|
0,07
|
0,07
|
0,07
|
0,07
|
|
1,2
|
-0,08
|
0,09
|
0,13
|
0,11
|
0,10
|
0,10
|
0,10
|
0,10
|
0,10
|
|
1,6
|
-0,08
|
0,10
|
0,14
|
0,11
|
0,11
|
0,11
|
0,11
|
0,11
|
0,11
|
Таблица 26
Поперечные
силы 
δ = 0,2
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
|
0,0
|
0,19
|
1,42
|
±00
|
-0,82
|
-0,36
|
-0,19
|
-0,10
|
-0,05
|
0,01
|
|
0,2
|
0,17
|
0,17
|
-0,10
|
-0,41
|
-0,28
|
-0,16
|
-0,09
|
-0,04
|
0,01
|
|
0,4
|
0,11
|
0,02
|
-0,05
|
0,15
|
-0,15
|
-,010
|
-0,06
|
-0,02
|
0,02
|
|
0,6
|
0,03
|
0,01
|
0,00
|
-0,04
|
-0,05
|
-0,04
|
-0,02
|
0,01
|
0,03
|
|
0,8
|
-0,04
|
0,00
|
0,04
|
0,03
|
0,01
|
0,01
|
0,02
|
0,02
|
0,04
|
|
1,0
|
-0,07
|
0,00
|
0,06
|
0,07
|
0,06
|
0,05
|
0,05
|
0,04
|
0,04
|
|
1,2
|
-0,08
|
0,00
|
0,05
|
0,09
|
0,08
|
0,07
|
0,06
|
0,05
|
0,05
|
|
1,6
|
-0,05
|
0,00
|
0,03
|
0,06
|
0,06
|
0,05
|
0,05
|
0,05
|
0,05
|
Таблица 27
Поперечные
силы 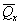
δ = 0,4
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
|
0,0
|
0,12
|
0,36
|
0,68
|
±∞
|
-0,79
|
-0,35
|
-0,20
|
-0,11
|
-0,03
|
0,01
|
|
0,2
|
0,10
|
0,22
|
0,29
|
-0,04
|
-0,38
|
-0,27
|
-0,17
|
-0,17
|
-0,02
|
0,01
|
|
0,4
|
0,04
|
0,06
|
0,08
|
-0,02
|
-0,14
|
-0,15
|
-0,11
|
-0,07
|
-0,01
|
0,01
|
|
0,6
|
0,00
|
0,02
|
0,04
|
0,01
|
-0,04
|
-0,06
|
-0,05
|
-0,03
|
0,00
|
0,01
|
|
0,8
|
-0,03
|
0,01
|
0,03
|
0,02
|
0,01
|
-0,01
|
-0,01
|
0,00
|
0,02
|
0,03
|
|
1,0
|
-0,04
|
0,00
|
0,03
|
0,04
|
0,04
|
0,03
|
0,02
|
0,02
|
0,03
|
0,03
|
|
1,2
|
-0,03
|
0,00
|
0,02
|
0,04
|
0,04
|
0,04
|
0,05
|
0,05
|
0,04
|
0,04
|
|
1,6
|
-0,01
|
0,00
|
0,02
|
0,03
|
0,04
|
0,05
|
0,06
|
0,05
|
0,05
|
0,04
|
Таблица 28
Поперечные
силы 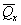
δ = 0,6
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
|
0,0
|
0,05
|
0,16
|
0,28
|
0,74
|
±∞
|
-0,68
|
-0,35
|
-0,20
|
-0,07
|
-0,02
|
0,00
|
|
0,2
|
0,04
|
0,12
|
0,21
|
0,35
|
-0,01
|
-0,38
|
-0,27
|
-0,18
|
-0,06
|
-0,02
|
0,00
|
|
0,4
|
0,02
|
0,06
|
0,11
|
0,12
|
0,00
|
-0,13
|
-0,15
|
-0,12
|
-0,05
|
-0,01
|
0,01
|
|
0,6
|
0,01
|
0,03
|
0,06
|
0,06
|
0,01
|
-0,05
|
-0,07
|
-0,07
|
-0,03
|
-0,01
|
0,01
|
|
0,8
|
0,00
|
0,02
|
0,05
|
0,05
|
0,02
|
0,00
|
-0,02
|
-0,03
|
-0,01
|
-0,01
|
0,02
|
|
1,0
|
-0,01
|
0,02
|
0,05
|
0,05
|
0,04
|
0,02
|
0,01
|
0,00
|
0,00
|
0,00
|
0,02
|
|
1,2
|
-0,01
|
0,01
|
0,04
|
0,04
|
0,04
|
0,04
|
0,03
|
0,02
|
0,02
|
0,02
|
0,03
|
|
1,6
|
-0,01
|
0,01
|
0,04
|
0,04
|
0,04
|
0,03
|
0,02
|
0,02
|
0,02
|
0,02
|
0,03
|
Таблица 29
Поперечные
силы 
δ = 0,8
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
|
0,0
|
0,01
|
0,08
|
0,15
|
0,33
|
0,77
|
±∞
|
-0,77
|
-0,36
|
-0,13
|
-0,05
|
-0,02
|
0,00
|
|
0,2
|
0,01
|
0,07
|
0,13
|
0,26
|
0,37
|
-0,04
|
-0,38
|
-0,28
|
-0,11
|
-0,05
|
-0,02
|
0,00
|
|
0,4
|
0,01
|
0,04
|
0,09
|
0,15
|
0,14
|
0,00
|
-0,13
|
-0,16
|
-0,09
|
-0,04
|
-0,01
|
0,00
|
|
0,6
|
0,00
|
0,03
|
0,06
|
0,08
|
0,07
|
0,01
|
-0,05
|
-0,08
|
-0,06
|
-0,03
|
-0,01
|
0,00
|
|
0,8
|
0,00
|
0,02
|
0,05
|
0,06
|
0,05
|
0,02
|
-0,02
|
-0,04
|
-0,03
|
-0,02
|
0,00
|
0,00
|
|
1,0
|
-0,01
|
0,02
|
0,05
|
0,05
|
0,04
|
0,02
|
0,00
|
-0,01
|
-0,01
|
0,00
|
0,00
|
0,00
|
|
1,2
|
-0,01
|
0,01
|
0,04
|
0,04
|
0,04
|
0,03
|
0,02
|
0,01
|
0,00
|
0,00
|
0,00
|
0,00
|
|
1,6
|
-0,01
|
0,01
|
0,04
|
0,04
|
0,03
|
0,03
|
0,02
|
0,02
|
0,01
|
0,01
|
0,01
|
0,00
|
Таблица 30
Поперечные
силы 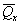
δ = 1,2
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
3,2
|
|
0,0
|
-0,01
|
0,03
|
0,07
|
0,13
|
0,22
|
0,27
|
0,78
|
±∞
|
-0,36
|
-0,14
|
-0,06
|
-0,03
|
-0,01
|
|
0,2
|
-0,01
|
0,03
|
0,06
|
0,12
|
0,19
|
0,29
|
0,39
|
0,00
|
-0,28
|
-0,13
|
-0,06
|
-0,03
|
-0,02
|
|
0,4
|
0,00
|
0,03
|
0,06
|
0,10
|
0,14
|
0,17
|
0,15
|
0,01
|
-0,16
|
-0,10
|
-0,05
|
-0,02
|
-0,02
|
|
0,6
|
0,01
|
0,03
|
0,05
|
0,08
|
0,10
|
0,10
|
0,08
|
0,01
|
-0,09
|
-0,07
|
-0,04
|
-0,02
|
-0,01
|
|
0,8
|
0,02
|
0,04
|
0,05
|
0,07
|
0,08
|
0,07
|
0,05
|
0,01
|
-0,04
|
-0,04
|
-0,03
|
-0,01
|
-0,01
|
|
1,0
|
0,03
|
0,03
|
0,05
|
0,06
|
0,06
|
0,05
|
0,04
|
0,02
|
-0,02
|
-0,02
|
-0,02
|
-0,01
|
0,00
|
|
1,2
|
0,03
|
0,03
|
0,04
|
0,06
|
0,05
|
0,04
|
0,04
|
0,02
|
0,00
|
-0,01
|
-0,01
|
0,00
|
0,00
|
|
1,6
|
0,02
|
0,03
|
0,04
|
0,05
|
0,04
|
0,05
|
0,03
|
0,01
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
Таблица 31
Поперечные силы 
δ = 1,6
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
3,2
|
3,6
|
|
0,0
|
-0,01
|
0,00
|
0,02
|
0,05
|
0,08
|
0,14
|
0,22
|
0,36
|
±∞
|
-0,36
|
-0,14
|
-0,06
|
-0,03
|
-0,01
|
|
0,2
|
-0,01
|
0,00
|
0,02
|
0,05
|
0,08
|
0,13
|
0,19
|
0,28
|
0,00
|
-0,29
|
-0,13
|
-0,06
|
-0,03
|
-0,01
|
|
0,4
|
-0,01
|
0,00
|
0,02
|
0,04
|
0,07
|
0,10
|
0,14
|
0,17
|
0,00
|
-0,17
|
-0,10
|
-0,05
|
-0,02
|
-0,01
|
|
0,6
|
0,00
|
0,00
|
0,02
|
0,03
|
0,05
|
0,07
|
0,09
|
0,10
|
0,00
|
-0,09
|
-0,06
|
-0,04
|
-0,02
|
-0,01
|
|
0,8
|
0,00
|
0,00
|
0,02
|
0,03
|
0,04
|
0,05
|
0,06
|
0,06
|
0,00
|
-0,05
|
-0,05
|
-0,03
|
-0,02
|
0,00
|
|
1,0
|
0,00
|
0,00
|
0,02
|
0,03
|
0,03
|
0,04
|
0,04
|
0,04
|
0,00
|
-0,03
|
-0,03
|
-0,02
|
-0,01
|
0,00
|
|
1,2
|
0,00
|
0,00
|
0,01
|
0,02
|
0,03
|
0,03
|
0,03
|
0,02
|
0,00
|
-0,02
|
-0,02
|
-0,02
|
-0,01
|
0,00
|
|
1,6
|
0,00
|
0,00
|
0,00
|
0,01
|
0,01
|
0,02
|
0,02
|
0,02
|
0,00
|
-0,01
|
-0,01
|
-0,01
|
-0,00
|
0,00
|
Таблица 32
Поперечные силы 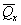
δ = 2,0
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
3,2
|
3,6
|
4,0
|
|
0,0
|
-0,01
|
0,00
|
0,01
|
0,02
|
0,04
|
0,06
|
0,10
|
0,14
|
0,37
|
±8
|
-0,37
|
-0,15
|
-0,07
|
-0,04
|
-0,02
|
|
0,2
|
-0,01
|
0,00
|
0,01
|
0,02
|
0,04
|
0,06
|
0,09
|
0,13
|
0,29
|
0,00
|
-0,29
|
-0,14
|
-0,07
|
-0,04
|
-0,02
|
|
0,4
|
-0,01
|
0,00
|
0,00
|
0,02
|
0,04
|
0,05
|
0,08
|
0,11
|
0,17
|
0,00
|
-0,17
|
-0,12
|
-0,06
|
-0,03
|
-0,02
|
|
0,6
|
-0,01
|
0,00
|
0,00
|
0,02
|
0,03
|
0,04
|
0,06
|
0,08
|
0,16
|
0,00
|
-0,10
|
-0,08
|
-0,05
|
-0,03
|
-0,02
|
|
0,8
|
0,00
|
0,00
|
0,00
|
0,01
|
0,02
|
0,03
|
0,05
|
0,05
|
0,05
|
0,00
|
-0,05
|
-0,06
|
-0,04
|
-0,03
|
-0,02
|
|
1,0
|
0,00
|
0,00
|
0,00
|
0,01
|
0,02
|
0,03
|
0,03
|
0,04
|
0,03
|
0,00
|
-0,03
|
-0,04
|
-0,03
|
-0,02
|
-0,01
|
|
1,2
|
0,00
|
0,00
|
0,00
|
0,01
|
0,01
|
0,02
|
0,02
|
0,03
|
0,02
|
0,00
|
-0,02
|
-0,03
|
-0,02
|
-0,02
|
-0,01
|
|
1,6
|
0,00
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,01
|
0,00
|
-0,01
|
-0,01
|
-0,01
|
-0,01
|
-0,00
|
Таблица 33
Поперечные силы 
δ = 0,0
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
|
0,0
|
-∞/0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0,2
|
-1,48
|
-1,17
|
-0,71
|
-0,24
|
-0,10
|
-0,04
|
-0,02
|
-0,01
|
-0,01
|
|
0,4
|
-0,58
|
-0,54
|
-0,46
|
-0,26
|
-0,13
|
-0,06
|
-0,03
|
-0,02
|
-0,01
|
|
0,6
|
-0,24
|
-0,24
|
-0,24
|
-0,17
|
-0,11
|
-0,06
|
-0,03
|
-0,02
|
-0,01
|
|
0,8
|
-0,04
|
-0,08
|
-0,09
|
-0,08
|
-0,06
|
-0,04
|
-0,02
|
-0,01
|
-0,01
|
|
1,0
|
0,08
|
0,04
|
0,02
|
-0,01
|
-0,02
|
-0,02
|
-0,01
|
-0,01
|
-0,02
|
|
1,2
|
0,11
|
0,08
|
0,05
|
0,02
|
0,00
|
-0,01
|
-0,01
|
-0,02
|
-0,03
|
|
1,6
|
0,07
|
0,06
|
0,04
|
0,02
|
0,00
|
-0,01
|
-0,02
|
-0,02
|
-0,03
|
Таблица 34
Поперечные силы 
δ = 0,1
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
|
0,0
|
0
|
-∞
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0,2
|
-0,74
|
-0,87
|
-0,69
|
-0,28
|
-0,13
|
-0,07
|
-0,04
|
-0,03
|
-0,01
|
|
0,4
|
-0,55
|
-0,52
|
-0,48
|
-0,32
|
-0,19
|
-0,12
|
-0,07
|
-0,05
|
-0,02
|
|
0,6
|
-0,48
|
-0,43
|
-0,38
|
-0,29
|
-0,20
|
-0,14
|
-0,10
|
-0,07
|
-0,02
|
|
0,8
|
-0,40
|
-0,35
|
-0,32
|
-0,25
|
-0,19
|
-0,14
|
-0,10
|
-0,07
|
-0,03
|
|
1,0
|
-0,30
|
-0,27
|
-0,25
|
-0,21
|
-0,17
|
-0,14
|
-0,10
|
-0,07
|
-0,03
|
|
1,2
|
-0,22
|
-0,20
|
-0,18
|
-0,17
|
-0,15
|
-0,12
|
-0,09
|
-0,06
|
-0,03
|
|
1,6
|
-0,14
|
-0,14
|
-0,14
|
-0,14
|
-0,12
|
-0,08
|
-0,05
|
0,00
|
-0,02
|
Таблица 35
Поперечные силы 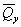
δ = 0,2
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
|
0,0
|
0
|
0
|
-∞
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0,2
|
-0,48
|
-0,70
|
-0,84
|
-0,42
|
-0,17
|
-0,09
|
-0,05
|
-0,03
|
-0,01
|
|
0,4
|
-0,47
|
-0,47
|
-0,48
|
-0,37
|
-0,22
|
-0,13
|
-0,8
|
-0,05
|
-0,02
|
|
0,6
|
-0,42
|
-0,40
|
-0,37
|
-0,30
|
-0,22
|
-0,15
|
-0,10
|
-0,07
|
-0,02
|
|
0,8
|
-0,36
|
-0,33
|
-0,30
|
-0,24
|
-0,19
|
-0,14
|
-0,10
|
-0,07
|
-0,03
|
|
1,0
|
-0,28
|
-0,25
|
-0,23
|
-0,20
|
-0,16
|
-0,13
|
-0,10
|
-0,07
|
-0,03
|
|
1,2
|
-0,17
|
-0,17
|
-0,17
|
-0,16
|
-0,14
|
-0,11
|
-0,08
|
-0
|
-0,02
|
|
1,6
|
-0,1
|
-0,1
|
-0,1
|
-0,1
|
-0,09
|
-0,07
|
-0,04
|
-0,01
|
-0,01
|
Таблица 36
Поперечные силы 
δ = 0,4
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
|
0,0
|
0
|
0
|
0
|
-∞
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0,2
|
-0,22
|
-0,29
|
-0,43
|
-0,81
|
-0,40
|
-0,16
|
-0,08
|
-0,04
|
-0,02
|
-0,01
|
|
0,4
|
-0,30
|
-0,33
|
-0,37
|
-0,42
|
-0,33
|
-0,20
|
-0,11
|
-0,07
|
-0,02
|
-0,01
|
|
0,6
|
-0,31
|
-0,31
|
-0,30
|
-0,29
|
-0,25
|
-0,18
|
-0,12
|
-0,08
|
-0,03
|
-0,01
|
|
0,8
|
-0,28
|
-0,26
|
-0,24
|
-0,22
|
-0,19
|
-0,15
|
-0,11
|
-0,08
|
-0,03
|
-0,01
|
|
1,0
|
-0,22
|
-0,21
|
-0,19
|
-0,17
|
-0,15
|
-0,12
|
-0,09
|
-0,07
|
-0,02
|
-0,00
|
|
1,2
|
-0,14
|
-0,14
|
-0,14
|
-0,13
|
-0,11
|
-0,10
|
-0,07
|
-0,05
|
-0,02
|
-0,00
|
|
1,6
|
-0,08
|
-0,08
|
-0,07
|
-0,07
|
-0,06
|
-0,05
|
-0,03
|
-0,01
|
-0,00
|
-0,00
|
Таблица 37
Поперечные силы 
δ = 0,6
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
|
0,0
|
0
|
0
|
0
|
0
|
-∞
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0,2
|
-0,11
|
-0,13
|
-0,18
|
-0,40
|
-0,80
|
-0,39
|
-0,15
|
-0,07
|
-0,02
|
-0,01
|
0,00
|
0,00
|
|
0,4
|
-0,19
|
-0,21
|
-0,23
|
-0,33
|
-0,40
|
-0,31
|
-0,18
|
-0,10
|
-0,13
|
-0,01
|
0,00
|
0,01
|
|
0,6
|
-0,21
|
-0,21
|
-0,22
|
-0,25
|
-0,26
|
-0,22
|
-0,16
|
-0,11
|
-0,04
|
-0,01
|
0,00
|
0,01
|
|
0,8
|
-0,20
|
-0,19
|
-0,19
|
-0,19
|
-0,19
|
-0,19
|
-0,13
|
-0,04
|
-0,04
|
-0,01
|
0,00
|
0,01
|
|
1,0
|
-0,17
|
-0,16
|
-0,16
|
-0,15
|
-0,14
|
-0,12
|
-0,10
|
-0,07
|
-0,04
|
-0,01
|
0,00
|
0,02
|
|
1,2
|
-0,12
|
-0,12
|
-0,12
|
-0,11
|
-0,10
|
-0,09
|
-0,07
|
-0,06
|
-0,03
|
-0,01
|
0,00
|
0,02
|
|
1,6
|
-0,05
|
-0,05
|
-0,05
|
-0,05
|
-0,04
|
-0,04
|
-0,03
|
-0,02
|
-0,03
|
0,00
|
0,01
|
0,00
|
Таблица 38
Поперечные силы 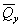
δ = 0,6
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
|
0,0
|
0
|
0
|
0
|
0
|
0
|
-∞
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0,2
|
-0,07
|
-0,08
|
-0,09
|
-0,16
|
-0,39
|
-0,79
|
-0,39
|
-0,15
|
-0,03
|
-0,01
|
0,00
|
0,00
|
|
0,4
|
-0,12
|
-0,13
|
-0,14
|
-0,20
|
-0,31
|
-0,38
|
-0,30
|
-0,18
|
-0,06
|
-0,02
|
0,00
|
0,00
|
|
0,6
|
-0,14
|
-0,14
|
-0,15
|
-0,18
|
-0,22
|
-0,24
|
-0,21
|
-0,15
|
-0,06
|
-0,02
|
-0,01
|
0,00
|
|
0,8
|
-0,14
|
-0,14
|
-0,14
|
0,15
|
-0,16
|
-0,16
|
-0,15
|
-0,12
|
-0,06
|
-0,02
|
-0,01
|
0,01
|
|
1,0
|
-0,11
|
-0,11
|
-0,11
|
0,11
|
-0,12
|
-0,11
|
-0,10
|
-0,09
|
-0,04
|
-0,02
|
0,00
|
0,01
|
|
1,2
|
-0,08
|
-0,08
|
-0,08
|
-0,08
|
-0,08
|
-0,08
|
-0,07
|
-0,06
|
-0,03
|
-0,02
|
0,00
|
0,01
|
|
1,6
|
-0,03
|
-0,03
|
-0,03
|
-0,03
|
-0,03
|
-0,03
|
-0,02
|
-0,02
|
-0,02
|
-0,01
|
0,00
|
0,00
|
Таблица 39
Поперечные силы 
δ = 1,2
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
3,2
|
|
0,0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
-∞
|
0
|
0
|
0
|
0
|
0
|
|
0,2
|
-0,03
|
-0,03
|
-0,03
|
-0,04
|
-0,07
|
-0,15
|
-0,38
|
-0,78
|
-0,13
|
-0,03
|
-0,01
|
-0,00
|
0,00
|
|
0,4
|
-0,06
|
-0,06
|
-0,06
|
-0,07
|
-0,11
|
-0,18
|
-0,29
|
-0,37
|
-0,17
|
-0,05
|
-0,02
|
-0,01
|
0,00
|
|
0,6
|
-0,08
|
-0,08
|
-0,08
|
-0,09
|
-0,11
|
-0,15
|
-0,20
|
-0,22
|
-0,15
|
-0,06
|
-0,02
|
-0,01
|
0,00
|
|
0,8
|
-0,08
|
-0,08
|
-0,08
|
-0,09
|
-0,10
|
-0,12
|
-0,14
|
-0,15
|
-0,11
|
-0,05
|
-0,02
|
-0,00
|
0,01
|
|
1,0
|
-0,09
|
-0,08
|
-0,08
|
-0,08
|
-0,09
|
-0,09
|
-0,10
|
-0,10
|
-0,09
|
-0,04
|
-0,02
|
-0,00
|
0,01
|
|
1,2
|
-0,08
|
-0,08
|
-0,07
|
-0,07
|
-0,07
|
-0,07
|
-0,07
|
-0,07
|
-0,05
|
-0,03
|
-0,02
|
-0,00
|
0,01
|
|
1,6
|
-0,04
|
-0,04
|
-0,04
|
-0,05
|
-0,06
|
-0,04
|
-0,05
|
-0,02
|
-0,02
|
-0,02
|
-0,01
|
-0,00
|
0,01
|
Таблица 40
Поперечные силы 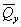
δ = 1,6
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
3,2
|
3,6
|
|
0,0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
-∞
|
0
|
0
|
0
|
0
|
0
|
|
0,2
|
-0,01
|
-0,01
|
-0,01
|
-0,01
|
-0,02
|
-0,03
|
-0,07
|
-0,14
|
-0,78
|
-0,13
|
-0,03
|
-0,01
|
0,00
|
0,00
|
|
0,4
|
-0,02
|
-0,02
|
-0,02
|
-0,03
|
-0,04
|
-0,06
|
-0,10
|
-0,17
|
-0,36
|
-0,17
|
-0,05
|
-0,02
|
-0,01
|
0,00
|
|
0,6
|
-0,03
|
-0,03
|
-0,03
|
-0,03
|
-0,04
|
-0,06
|
-0,09
|
-0,14
|
-0,22
|
-0,15
|
-0,06
|
-0,02
|
-0,01
|
0,00
|
|
0,8
|
-0,04
|
-0,04
|
-0,04
|
-0,04
|
-0,04
|
-0,06
|
-0,08
|
-0,11
|
-0,14
|
-0,10
|
-0,05
|
-0,02
|
-0,01
|
0,00
|
|
1,0
|
-0,04
|
-0,04
|
-0,04
|
-0,04
|
-0,04
|
-0,05
|
-0,06
|
-0,08
|
-0,10
|
-0,09
|
-0,04
|
-0,02
|
-0,01
|
0,00
|
|
1,2
|
-0,03
|
-0,03
|
-0,03
|
-0,03
|
-0,03
|
-0,04
|
-0,04
|
-0,05
|
-0,06
|
-0,05
|
-0,03
|
-0,02
|
-0,01
|
0,00
|
|
1,6
|
-0,02
|
-0,02
|
-0,02
|
-0,02
|
-0,02
|
-0,02
|
-0,02
|
-0,02
|
-0,02
|
-0,02
|
-0,02
|
-0,01
|
0,00
|
0,00
|
Таблица 41
Поперечные силы 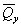
δ = 2,0
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
3,2
|
3,6
|
4,0
|
|
0,0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
-∞
|
0
|
0
|
0
|
0
|
0
|
|
0,2
|
0,00
|
-0,01
|
-0,01
|
-0,01
|
-0,01
|
-0,01
|
-0,02
|
-0,03
|
-0,13
|
-0,78
|
-0,13
|
-0,03
|
-0,01
|
-0,01
|
0,00
|
|
0,4
|
-0,01
|
-0,01
|
-0,01
|
-0,01
|
-0,01
|
-0,02
|
-0,03
|
-0,05
|
-0,17
|
-0,37
|
-0,17
|
-0,05
|
-0,02
|
-0,01
|
0,00
|
|
0,6
|
-0,01
|
-0,01
|
-0,01
|
-0,01
|
-0,02
|
-0,03
|
-0,04
|
-0,06
|
-0,15
|
-0,22
|
-0,135
|
-0,06
|
-0,03
|
-0,01
|
-0,01
|
|
0,8
|
-0,01
|
-0,01
|
-0,01
|
-0,01
|
-0,02
|
-0,03
|
-0,04
|
-0,05
|
-0,11
|
-0,14
|
-0,11
|
-0,05
|
-0,03
|
-0,01
|
-0,01
|
|
1,0
|
-0,01
|
-0,01
|
-0,01
|
-0,01
|
-0,02
|
-0,03
|
-0,03
|
-0,04
|
-0,09
|
-0,10
|
-0,09
|
-0,04
|
-0,03
|
-0,01
|
-0,01
|
|
1,2
|
-0,01
|
-0,01
|
-0,01
|
-0,01
|
-0,01
|
-0,02
|
-0,03
|
-0,03
|
-0,05
|
-0,06
|
-0,05
|
-0,03
|
-0,02
|
-0,01
|
-0,01
|
|
1,6
|
-0,01
|
-0,01
|
-0,01
|
-0,01
|
-0,01
|
-0,01
|
-0,02
|
-0,02
|
-0,03
|
-0,04
|
-0,03
|
-0,02
|
-0,01
|
-0,01
|
0,00
|
Таблица 42
Поперечные силы 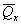
δ > 2
|
η
|
ξ
|
η
|
ξ
|
|
0,0
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,4
|
1,6
|
1,8
|
2,0
|
2,2
|
2,4
|
2,6
|
2,8
|
|
0,0
|
∞
|
0,779
|
0,367
|
0,224
|
0,150
|
0,105
|
0,074
|
0,053
|
0,038
|
0,027
|
0,019
|
0,013
|
0,0
|
0,008
|
0,005
|
0,002
|
|
0,2
|
0
|
0,385
|
0,294
|
0,203
|
0,141
|
0,100
|
0,071
|
0,052
|
0,037
|
0,027
|
0,019
|
0,013
|
0,2
|
0,008
|
0,005
|
0,002
|
|
0,4
|
0
|
0,132
|
0,172
|
0,150
|
0,117
|
0,086
|
0,065
|
0,047
|
0,034
|
0,024
|
0,018
|
0,012
|
0,4
|
0,008
|
0,005
|
0,002
|
|
0,6
|
0
|
0,064
|
0,100
|
0,098
|
0,084
|
0,068
|
0,053
|
0,041
|
0,030
|
0,022
|
0,015
|
0,011
|
0,6
|
0,007
|
0,004
|
0,001
|
|
0,8
|
0
|
0,035
|
0,058
|
0,063
|
0,060
|
0,052
|
0,040
|
0,032
|
0,025
|
0,018
|
0,013
|
0,008
|
0,8
|
0,006
|
0,003
|
0,001
|
|
1,0
|
0
|
0,020
|
0,034
|
0,041
|
0,041
|
0,037
|
0,032
|
0,025
|
0,019
|
0,015
|
0,011
|
0,007
|
1,0
|
0,005
|
0,002
|
0,000
|
|
1,2
|
0
|
0,012
|
0,022
|
0,026
|
0,027
|
0,026
|
0,023
|
0,019
|
0,015
|
0,012
|
0,009
|
0,005
|
1,2
|
0,004
|
0,001
|
|
|
1,4
|
0
|
0,007
|
0,013
|
0,017
|
0,018
|
0,018
|
0,016
|
0,014
|
0,011
|
0,009
|
0,006
|
0,004
|
1,4
|
0,002
|
0,000
|
|
|
1,6
|
0
|
0,005
|
0,008
|
0,011
|
0,013
|
0,012
|
0,011
|
0,010
|
0,008
|
0,006
|
0,005
|
0,002
|
1,6
|
0,001
|
|
|
|
1,8
|
0
|
0,003
|
0,005
|
0,007
|
0,008
|
0,008
|
0,008
|
0,007
|
0,005
|
0,004
|
0,003
|
0,001
|
|
|
|
|
|
2,0
|
0
|
0,002
|
0,004
|
0,005
|
0,005
|
0,006
|
0,005
|
0,005
|
0,004
|
0,003
|
0,002
|
0,000
|
|
|
|
|
|
2,2
|
0
|
0,001
|
0,002
|
0,003
|
0,003
|
0,003
|
0,003
|
0,003
|
0,002
|
0,001
|
0,000
|
|
|
|
|
|
|
2,4
|
0
|
0,001
|
0,001
|
0,002
|
0,002
|
0,002
|
0,002
|
0,001
|
0,001
|
0,000
|
|
|
|
|
|
|
|
2,6
|
0
|
0,000
|
0,001
|
0,001
|
0,001
|
0,001
|
0,000
|
0,000
|
0,000
|
|
|
|
|
|
|
|
|
2,8
|
0
|
0,000
|
0,000
|
0,000
|
0,000
|
0,000
|
0,000
|
0,000
|
0,000
|
|
|
|
|
|
|
|
Таблица 43
Вводы в табл. 24 - 42
|
Расстояние нагрузки
от края
плиты δki
|
Вводы в табл. 24 - 42
|
Примечания
|
|
ξ
|
η
|
|
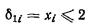
|
xn
|
yn - yi
|
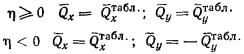
|
|
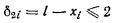
|
l - xn
|
yn - yi
|
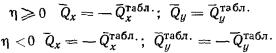
|
|
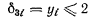
|
yn
|
xn - xi
|
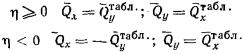
|
|

|
b - yn
|
xn - xi
|

|
|

|
xi - xn
|
yi - yn
|
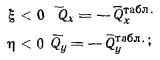
|
Для определения величины 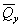 по табл.
42 меняют вводы ξ на η и обратно. по табл.
42 меняют вводы ξ на η и обратно.
Безразмерную величину 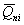 определяют по табл. 42, если все значения δki > 2. определяют по табл. 42, если все значения δki > 2.
При определении безразмерных величин 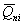 по табл.
24 - 42 может потребоваться
интерполяция табличных значений между бесконечно большой величиной и
расположенной от нее справа или слева. В этом случае выбирают соответственно
левое или правое значение безразмерной величины по табл.
24 - 42 может потребоваться
интерполяция табличных значений между бесконечно большой величиной и
расположенной от нее справа или слева. В этом случае выбирают соответственно
левое или правое значение безразмерной величины 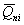 . .
Если величины ξ и η окажутся больше табличных значений, то принимают 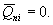
3.17. Вычисление предварительных размеров плитного
фундамента здания с несущими стенами выполняют по указаниям пп.
3.3 - 3.5
и 3.7
следующим образом:
1) принимают толщину
фундамента h в интервале от минимальной hmin до максимальной hmax
заданных величин с шагом 50 мм;
2) вычисляют величину
поперечной силы Q, максимально возможную по условию (42) прочности наклонных сечений при принятой толщине
фундамента;
3) находят по формуле (37) упругую характеристику плитного фундамента;
4) определяют поперечную силу Qn в заданной точке n фундамента по рекомендациям п. 3.16 и сравнивают с
величиной Q;
5) повторяют вычисления п. 4
для точки n +
1, если Qn
≤ Q;
6) увеличивают толщину
фундамента h так, как это указано в п.
3.17.1, если Qn > Q, и повторяют
пп. 3.17.2 - 3.17.4;
7) вычисления по пп. 3.17.1 -
3.17.6 продолжают до тех пор, пока толщина фундамента h ≤ hmax;
8) увеличивают толщину
фундамента под стенами, если при принятой максимальной толщине фундамента hmax
поперечная сила Q в
точке n, расположенной у грани стены, оказалась больше
максимально возможной величины Q. Величину
местных утолщений hм фундамента
под стенами принимают в пределах от нулевой до максимальной заданной величины с
шагом 50 мм и повторяют пп. 2 - 4;
9) для уменьшения поперечных
сил Qn в точках n фундамента под гранями наружных стен при Qn
> Q , h = hmax, hм = hм max увеличивают с шагом 150 мм длины консольных участков lk фундамента от значений, принятых
в результате расчета по указаниям разд. 2, до максимальных
заданных величин lk mах;

Рис.
8. План плитного фундамента каркасного здания
i, j - номера рядов сетки колонн; х1, у1, х2, у2 -
системы координат; l1, l2,
l3, l4 - длины консольных участков фундамента
10) определяют осадки центров n-х
загруженных участков фундамента по рекомендациям пп.
3.10, 3.11 и
проверяют относительные разности средних осадок участков фундамента под
параллельными стенами;
11) толщину плиты увеличивают с шагом 50
мм до максимального заданного значения hmах и
повторяют п. 10, если относительная разность осадок превышает заданную
предельную величину.
3.18. Для унификации опалубочных и арматурных изделий
принимают размеры плитного фундамента кратными в плане 300 мм, по высоте 50 мм
(при минимальной толщине фундамента 300 мм).
Пример вычисления на ЭВМ по программе «РАПОРТ» предварительных размеров
плитного фундамента каркасного здания
Требуется определить по условию
минимального объема бетона предварительные размеры в плане и толщину плитного
фундамента каркасного здания, а также квадратных в плане монолитных
подколонников, необходимые для статического расчета плитного фундамента на ЭВМ
по программам, перечисленным в прил.
1.
План плитного фундамента каркасного
здания с нагрузками на колонны, кН, приведен на рис. 8.
Вычисления выполняем на ЭВМ по программе
«РАПОРТ». Исходные данные к расчету составляем с использованием результатов
расчета деформаций основания фундамента, выполненных по указаниям разд. 2
с помощью программы «GEST-82».
Для определения предварительных
размеров плитного фундамента на ЭВМ по программе «РАПОРТ» задаем следующие
исходные данные: количество рядов колонн m = 6 по оси х1 и n = 4 по оси
y1; расстояния между осями крайних рядов колонн l0 = 30 м по оси x1 и b0 = 18 м
по оси y1; расчетное сопротивление бетона марки
М 300 на осевое растяжение Rр = 1000
кПа; защитный слой бетона с = 0,035
м; модуль упругости бетона Eб =
3,15·107 кПа; коэффициент бокового расширения бетона μб
= 0,17; осредненный приведенный модуль деформации основания Eпрср = 38100
кПа; коэффициент бокового расширения грунта v0 = 0,329;
толщину сжимаемого слоя основания H = 9,3 м; координаты центров колонн в системе
координат x1, y1, м (табл.
44); вертикальные нагрузки на колонны, кН (табл. 45); признаки продавливания
фундамента надколонниками соответственно 1
- по четырем, 2 - по
трем, 3 - по двум граням (табл.
46); среднее реактивное давление на участках фундамента, примыкающих к
колоннам, кПа (табл. 47); длины
консольных участков фундамента 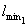 = = 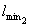 = = 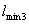 . = . =  = 1,5 м (по
расчету деформаций основания) и = 1,5 м (по
расчету деформаций основания) и  = =  = =  . = . = 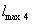 = 3 м (по
конструктивным соображениям); длину стороны квадратного сечения колонны = 3 м (по
конструктивным соображениям); длину стороны квадратного сечения колонны  м; максимальную длину
стороны квадратного подколонника м; максимальную длину
стороны квадратного подколонника  м; максимальную
толщину подколонника м; максимальную
толщину подколонника  м предельную относительную
разность осадок колонны в продольном и поперечном направлении 0,006. м предельную относительную
разность осадок колонны в продольном и поперечном направлении 0,006.
Таблица 44
|
Номера рядов колонн i
|
Координаты центров колонн j
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
x1
|
y1
|
x1
|
y1
|
x1
|
y1
|
x1
|
y1
|
x1
|
y1
|
x1
|
y1
|
|
1
|
0
|
0
|
6
|
0
|
12
|
0
|
18
|
0
|
24
|
0
|
30
|
0
|
|
2
|
0
|
6
|
6
|
6
|
12
|
6
|
18
|
6
|
24
|
6
|
30
|
6
|
|
3
|
0
|
12
|
6
|
12
|
12
|
12
|
18
|
12
|
24
|
12
|
30
|
12
|
|
4
|
0
|
18
|
6
|
18
|
12
|
18
|
18
|
18
|
24
|
18
|
30
|
18
|
Таблица 45
|
Номера рядов колонн i
|
Вертикальные нагрузки Рij на колонны ряда j
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
3500
|
4500
|
4500
|
4500
|
4500
|
3500
|
|
2
|
3500
|
6500
|
6500
|
6500
|
6500
|
3500
|
|
3
|
3500
|
6500
|
6500
|
6500
|
6500
|
6500
|
|
4
|
3500
|
4500
|
4500
|
4500
|
4500
|
3500
|
Таблица 46
|
Номера рядов колонн i
|
Признаки продавливания подколонников ряда j
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
3
|
2
|
2
|
2
|
2
|
3
|
|
2
|
2
|
1
|
1
|
1
|
1
|
2
|
|
3
|
2
|
1
|
1
|
1
|
1
|
2
|
|
4
|
3
|
2
|
2
|
2
|
2
|
3
|
Таблица 47
|
Номера рядов колонн i
|
Среднее реактивное давление на участках
фундамента,
примыкающих к колоннам ряда j
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
172,84
|
166,67
|
166,67
|
166,67
|
166,67
|
172,84
|
|
2
|
129,63
|
180,56
|
180,56
|
180,56
|
180,56
|
129,63
|
|
3
|
129,63
|
180,56
|
180,56
|
180,56
|
180,56
|
129,63
|
|
4
|
172,84
|
166,67
|
166,67
|
166,67
|
166,67
|
172,84
|
В результате расчета найдены и
выданы на АЦПУ ЭВМ следующие величины: упругая характеристика фундамента L = 1,73 м;
осредненный приведенный модуль деформации основания с корректирующим
коэффициентом mE Eпрср =
117254,6 кПа; толщина подколонников hп = 0,9 м;
длина стороны квадратного подколонника aij
= bij, м (табл.
48); длина консолей l1 = l2 = l3 = l4 = l,5 м; объем
бетона плитного фундамента с подколонниками 439,43 м3; стоимость
фундамента 24168 руб.; толщина h = 0,5 м, длина l = 33 м и ширина b = 21 м фундамента.
Таблица 48
|
Номера рядов колонн i
|
Длина стороны квадратного подколонника ряда
j
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
2
|
2
|
2
|
2
|
2
|
2
|
|
2
|
2
|
2,2
|
2,2
|
2,2
|
2,2
|
2
|
|
3
|
2
|
2,2
|
2,2
|
2,2
|
2,2
|
2
|
|
4
|
2
|
2
|
2
|
2
|
2
|
2
|
4. ОПРЕДЕЛЕНИЕ
КОЭФФИЦИЕНТОВ ЖЕСТКОСТИ ОСНОВАНИЯ ПЛИТНОГО ФУНДАМЕНТА
4.1. Рекомендации настоящего раздела составлены для
определения деформационной характеристики (переменного коэффициента жесткости
при сжатии) неоднородного в плане и по глубине основания на контакте с плитным
фундаментом.
4.2. Вычисление переменного коэффициента жесткости
основания выполняют на стадии подготовки исходной информации к раздельному либо
совместному расчету плитного фундамента на сжимаемом основании и
надфундаментного строения.
4.3. При определении переменного коэффициента жесткости
основания учитывают основные параметры физико-механических свойств грунтов,
неоднородность геологического строения основания, распределительные свойства
грунта, размеры, форму и жесткость плитного фундамента, влияние нагрузок,
передаваемых на основание соседними фундаментами (если их строят одновременно
или позднее рассчитываемого), а также величину и действительную схему
размещения на фундаменте заданных нагрузок.
4.4. Переменный коэффициент k(x, у) жесткости основания, аналогичный по смыслу
винклеровскому коэффициенту постели, определяют, исходя из ожидаемых осадок S(x, у) участков фундамента и возможных величин реактивных
давлений р(х, у) на
этих же участках фундамента, по формуле
4.5. При определении
переменного коэффициента жесткости основания возможна приближенная оценка
влияния жесткости плитного фундамента на осадки основания и реактивные
давления.
В этом случае переменный коэффициент
жесткости kqf основания
фундамента, прямоугольной формы в плане, несущего нагрузку от колонн здания или
сооружения, расположенных по прямоугольной сетке с переменным шагом в двух
направлениях, находят в узлах qf основной
прямоугольной сетки, нанесенной на план фундамента (рис.
3), вручную по формуле (45) или на ЭВМ по программе «ЖОК», основные сведения о которой даны в прил.
1:
|
kqf = pqf/(Sqf αqf),
|
(45)
|
где
pqf - давление на основание, найденное по указаниям п. 4.6 с
учетом влияния жесткости фундамента на распределение реактивных давлений;
Sqf - осадка неоднородного в плане многослойного основания
от среднего давления р, равномерно
распределенного в пределах плана фундамента, вычисленная по указаниям разд. 2
вручную или на ЭВМ по программе
«GEST-82», т.е. без учета влияния жесткости фундамента на
характер эпюр реактивных давлений и осадок основания;
αqf - коэффициент влияния жесткости фундамента на характер
эпюры осадок основания, определяемый по формуле
В формуле (46) приняты следующие
обозначения:
Sqf1 - осадка однородного основания, нагруженного в пределах
плана фундамента равномерно распределенным средним давлением р, вычисляемая по п. (4.7);
Sqf2 - осадка
плитного фундамента, лежащего на однородном основании и несущего нагрузку от
здания или сооружения, определяемая по п.
3.10.
4.6. Давление рqf на
основание в точке qf под подошвой
плитного фундамента вычисляют по формуле
|

|
(47)
|
где
L -
упругая характеристика фундамента, вычисляемая по формуле (37);
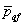 - безразмерная величина, определяемая по табл. 49 - 58 в
зависимости от найденных по формулам табл.
22 приведенных (в долях от L) расстояния δkij,
нагрузки Pij от
ближайшего края фундамента и величин ξ, η, найденных по координатам точки
ij(xij, уij) приложения нагрузки Pij и рассматриваемой точки qf(xqf, yqf) фундамента в системе координат, начало которой принято
в левом верхнем углу фундамента; ось х направлена вдоль длинной стороны вправо; ось у вдоль короткой стороны вниз по плану
фундамента (см. рис.
3); - безразмерная величина, определяемая по табл. 49 - 58 в
зависимости от найденных по формулам табл.
22 приведенных (в долях от L) расстояния δkij,
нагрузки Pij от
ближайшего края фундамента и величин ξ, η, найденных по координатам точки
ij(xij, уij) приложения нагрузки Pij и рассматриваемой точки qf(xqf, yqf) фундамента в системе координат, начало которой принято
в левом верхнем углу фундамента; ось х направлена вдоль длинной стороны вправо; ось у вдоль короткой стороны вниз по плану
фундамента (см. рис.
3);
Pij - нагрузка от колонн или участков стен здания либо
сооружения.
Безразмерную величину  определяют по табл. 58, если все значения δkij > 2. Если величины ξ или η окажутся больше табличных, то принимают определяют по табл. 58, если все значения δkij > 2. Если величины ξ или η окажутся больше табличных, то принимают 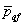 = 0. Из величин = 0. Из величин  , полученных по табл. 49
- 57, выбирают большую. , полученных по табл. 49
- 57, выбирают большую.
4.7. Осадки Sqf1 однородного основания, нагруженного в пределах плана
фундамента средним давлением р,
определяют с использованием метода угловых точек и следующей формулы, принимая
основание однородным в плане с расчетной схемой в виде линейно-деформируемого
слоя
где
b - ширина плитного фундамента;
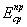 и μср - соответственно осредненный приведенный модуль
деформации основания и осредненный коэффициент бокового давления грунта,
определяемые по рекомендациям разд. 2; и μср - соответственно осредненный приведенный модуль
деформации основания и осредненный коэффициент бокового давления грунта,
определяемые по рекомендациям разд. 2;
mЕ -
корректирующий коэффициент, введенный в формулу (48)
для сближения расчетных осадок фундамента на линейно-деформируемом
полупространстве и слое, вычисляемый по рекомендациям п. 3.11;
ki - коэффициент, определяемый для основания в виде
линейно-деформируемого полупространства по табл.
59 в зависимости от отношения сторон фундамента n = l/b для следующих точек i фундамента: i = 0 - центра; 1 - середины большей стороны; 2 - середины меньшей стороны; 3 - угловой точки.
Таблица 49
Реактивные
давления 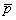
δ = 0
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
|
0,0
|
1,06
|
0,81
|
0,63
|
0,39
|
0,25
|
0,17
|
0,11
|
0,06
|
0,00
|
-0,03
|
|
0,2
|
1,05
|
0,80
|
0,62
|
0,38
|
0,25
|
0,16
|
0,11
|
0,06
|
0,00
|
-0,03
|
|
0,4
|
1,01
|
0,77
|
0,59
|
0,36
|
0,23
|
0,15
|
0,09
|
0,05
|
-0,01
|
-0,03
|
|
0,6
|
0,96
|
0,71
|
0,54
|
0,32
|
0,20
|
0,12
|
0,07
|
0,03
|
-0,02
|
-0,03
|
|
0,8
|
0,88
|
0,65
|
0,48
|
0,27
|
0,16
|
0,09
|
0,05
|
0,01
|
-0,03
|
-0,03
|
|
1,0
|
0,79
|
0,56
|
0,42
|
0,22
|
0,12
|
0,06
|
0,02
|
-0,01
|
-0,04
|
-0,03
|
|
1,2
|
0,07
|
0,50
|
0,35
|
0,16
|
0,07
|
0,02
|
-0,01
|
-0,03
|
-0,05
|
-0,03
|
|
1,6
|
0,50
|
0,32
|
0,19
|
0,06
|
0,00
|
0,00
|
-0,01
|
-0,02
|
-0,02
|
-0,02
|
|
2,0
|
0,30
|
0,15
|
0,05
|
-0,03
|
-0,04
|
-0,02
|
-0,01
|
-0,01
|
-0,01
|
-0,01
|
Таблица 50
Реактивные
давления 
δ = 0,1
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
|
0,0
|
0,98
|
0,75
|
0,58
|
0,37
|
0,25
|
0,18
|
0,12
|
0,06
|
0,02
|
0,01
|
|
0,2
|
0,97
|
0,74
|
0,57
|
0,36
|
0,25
|
0,18
|
0,12
|
0,06
|
0,02
|
0,01
|
|
0,4
|
0,95
|
0,72
|
0,55
|
0,33
|
0,23
|
0,15
|
0,10
|
0,05
|
0,01
|
0,01
|
|
0,6
|
0,89
|
0,66
|
0,50
|
0,30
|
0,20
|
0,12
|
0,06
|
0,04
|
0,01
|
0,01
|
|
0,8
|
0,82
|
0,60
|
0,45
|
0,26
|
0,16
|
0,09
|
0,05
|
0,04
|
0,01
|
0,01
|
|
1,0
|
0,74
|
0,52
|
0,39
|
0,22
|
0,12
|
0,07
|
0,05
|
0,04
|
0,01
|
0,01
|
|
1,2
|
0,65
|
0,47
|
0,32
|
0,18
|
0,09
|
0,06
|
0,04
|
0,04
|
0,00
|
0,00
|
|
1,6
|
0,47
|
0,30
|
0,18
|
0,11
|
0,05
|
0,03
|
0,03
|
0,03
|
0,00
|
-0,01
|
|
2,0
|
0,28
|
0,14
|
0,07
|
0,04
|
0,03
|
0,03
|
0,03
|
0,02
|
0,00
|
-0,02
|
Таблица 51
Реактивные
давления 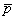
δ = 0,2
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
|
0,0
|
0,91
|
0,70
|
0,53
|
0,34
|
0,25
|
0,18
|
0,13
|
0,07
|
0,03
|
0,01
|
0,01
|
|
0,2
|
0,90
|
0,69
|
0,52
|
0,34
|
0,25
|
0,18
|
0,13
|
0,07
|
0,03
|
0,01
|
0,01
|
|
0,4
|
0,88
|
0,66
|
0,51
|
0,31
|
0,23
|
0,15
|
0,11
|
0,06
|
0,03
|
0,01
|
0,01
|
|
0,6
|
0,82
|
0,61
|
0,47
|
0,29
|
0,20
|
0,13
|
0,08
|
0,06
|
0,03
|
0,01
|
0,01
|
|
0,8
|
0,76
|
0,56
|
0,41
|
0,25
|
0,16
|
0,09
|
0,07
|
0,05
|
0,02
|
0,01
|
0,01
|
|
1,0
|
0,69
|
0,48
|
0,36
|
0,21
|
0,12
|
0,08
|
0,07
|
0,05
|
0,02
|
0,01
|
0,01
|
|
1,2
|
0,61
|
0,44
|
0,30
|
0,17
|
0,10
|
0,08
|
0,06
|
0,05
|
0,02
|
0,01
|
0,01
|
|
1,6
|
0,44
|
0,28
|
0,17
|
0,12
|
0,07
|
0,07
|
0,05
|
0,04
|
0,02
|
0,01
|
0,01
|
|
2,0
|
0,27
|
0,13
|
0,08
|
0,06
|
0,05
|
0,05
|
0,05
|
0,04
|
0,02
|
0,01
|
0,00
|
Таблица
52
Реактивные давления 
δ = 0,4
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
|
0,0
|
0,76
|
0,58
|
0,45
|
0,30
|
0,23
|
0,18
|
0,14
|
0,11
|
0,06
|
0,03
|
0,02
|
|
0,2
|
0,76
|
0,58
|
0,45
|
0,30
|
0,23
|
0,18
|
0,13
|
0,11
|
0,06
|
0,03
|
0,02
|
|
0,4
|
0,74
|
0,55
|
0,43
|
0,27
|
0,22
|
0,17
|
0,12
|
0,10
|
0,05
|
0,02
|
0,02
|
|
0,6
|
0,70
|
0,52
|
0,39
|
0,25
|
0,20
|
0,14
|
0,11
|
0,09
|
0,05
|
0,02
|
0,02
|
|
0,8
|
0,64
|
0,47
|
0,34
|
0,22
|
0,15
|
0,11
|
0,10
|
0,08
|
0,04
|
0,02
|
0,02
|
|
1,0
|
0,58
|
0,41
|
0,30
|
0,19
|
0,12
|
0,10
|
0,09
|
0,07
|
0,04
|
0,02
|
0,01
|
|
1,2
|
0,51
|
0,37
|
0,25
|
0,15
|
0,11
|
0,10
|
0,08
|
0,07
|
0,04
|
0,02
|
0,01
|
|
1,6
|
0,37
|
0,25
|
0,15
|
0,13
|
0,09
|
0,09
|
0,08
|
0,06
|
0,03
|
0,01
|
0,01
|
|
2,0
|
0,23
|
0,12
|
0,10
|
0,09
|
0,08
|
0,08
|
0,07
|
0,06
|
0,03
|
0,01
|
0,00
|
Таблица
53
Реактивные давления 
δ = 0,6
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
|
0,0
|
0,62
|
0,47
|
0,36
|
0,25
|
0,21
|
0,17
|
0,15
|
0,13
|
0,09
|
0,06
|
0,04
|
0,03
|
|
0,2
|
0,62
|
0,47
|
0,36
|
0,25
|
0,21
|
0,16
|
0,14
|
0,12
|
0,08
|
0,06
|
0,04
|
0,03
|
|
0,4
|
0,60
|
0,44
|
0,34
|
0,23
|
0,20
|
0,15
|
0,14
|
0,12
|
0,08
|
0,05
|
0,03
|
0,03
|
|
0,6
|
0,57
|
0,42
|
0,32
|
0,21
|
0,18
|
0,14
|
0,12
|
0,11
|
0,08
|
0,05
|
0,03
|
0,03
|
|
0,8
|
0,51
|
0,39
|
0,28
|
0,19
|
0,14
|
0,12
|
0,11
|
0,10
|
0,07
|
0,04
|
0,03
|
0,03
|
|
1,0
|
0,47
|
0,34
|
0,24
|
0,17
|
0,12
|
0,11
|
0,10
|
0,09
|
0,06
|
0,03
|
0,02
|
0,02
|
|
1,2
|
0,42
|
0,31
|
0,21
|
0,14
|
0,11
|
0,10
|
0,09
|
0,08
|
0,05
|
0,03
|
0,02
|
0,01
|
|
1,6
|
0,31
|
0,21
|
0,15
|
0,13
|
0,11
|
0,10
|
0,08
|
0,07
|
0,05
|
0,02
|
0,01
|
0,00
|
|
2,0
|
0,20
|
0,10
|
0,10
|
0,10
|
0,10
|
0,09
|
0,08
|
0,07
|
0,04
|
0,02
|
0,00
|
-0,01
|
Таблица
54
Реактивные давления 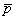
δ
= 0,8
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
|
0,0
|
0,48
|
0,36
|
0,28
|
0,21
|
0,18
|
0,17
|
0,16
|
0,14
|
0,11
|
0,07
|
0,05
|
0,03
|
|
0,2
|
0,48
|
0,36
|
0,28
|
0,20
|
0,18
|
0,17
|
0,16
|
0,14
|
0,11
|
0,07
|
0,05
|
0,03
|
|
0,4
|
0,47
|
0,34
|
0,27
|
0,19
|
0,17
|
0,16
|
0,15
|
0,13
|
0,10
|
0,07
|
0,04
|
0,03
|
|
0,6
|
0,44
|
0,33
|
0,26
|
0,18
|
0,16
|
0,15
|
0,13
|
0,12
|
0,10
|
0,06
|
0,03
|
0,03
|
|
0,8
|
0,40
|
0,31
|
0,22
|
0,15
|
0,14
|
0,13
|
0,12
|
0,11
|
0,03
|
0,06
|
0,03
|
0,02
|
|
1,0
|
0,37
|
0,26
|
0,19
|
0,14
|
0,12
|
0,11
|
0,10
|
0,10
|
0,07
|
0,05
|
0,02
|
0,02
|
|
1,2
|
0,33
|
0,25
|
0,16
|
0,12
|
0,11
|
0,10
|
0,09
|
0,08
|
0,06
|
0,04
|
0,02
|
0,01
|
|
1,6
|
0,25
|
0,18
|
0,11
|
0,11
|
0,10
|
0,10
|
0,09
|
0,08
|
0,05
|
0,03
|
0,02
|
0,01
|
|
2,0
|
0,17
|
0,09
|
0,10
|
0,10
|
0,09
|
0,09
|
0,08
|
0,07
|
0,05
|
0,03
|
0,01
|
0,00
|
Таблица
55
Реактивные давления 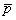
δ = 1,2
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
3,2
|
|
0,0
|
0,24
|
0,19
|
0,15
|
0,12
|
0,13
|
0,14
|
0,16
|
0,17
|
0,16
|
0,12
|
0,07
|
0,03
|
0,03
|
|
0,2
|
0,24
|
0,19
|
0,15
|
0,12
|
0,12
|
0,14
|
0,15
|
0,16
|
0,15
|
0,11
|
0,07
|
0,03
|
0,03
|
|
0,4
|
0,23
|
0,18
|
0,14
|
0,11
|
0,11
|
0,13
|
0,14
|
0,15
|
0,14
|
0,10
|
0,06
|
0,03
|
0,03
|
|
0,6
|
0,22
|
0,17
|
0,13
|
0,09
|
0,10
|
0,11
|
0,12
|
0,13
|
0,13
|
0,09
|
0,05
|
0,03
|
0,03
|
|
0,8
|
0,21
|
0,16
|
0,11
|
0,08
|
0,08
|
0,09
|
0,10
|
0,11
|
0,10
|
0,08
|
0,05
|
0,03
|
0,03
|
|
1,0
|
0,18
|
0,14
|
0,10
|
0,06
|
0,06
|
0,07
|
0,08
|
0,09
|
0,08
|
0,06
|
0,04
|
0,03
|
0,03
|
|
1,2
|
0,17
|
0,13
|
0,09
|
0,05
|
0,04
|
0,05
|
0,06
|
0,07
|
0,07
|
0,05
|
0,03
|
0,02
|
0,01
|
|
1,6
|
0,15
|
0,11
|
0,07
|
0,05
|
0,04
|
0,05
|
0,05
|
0,06
|
0,05
|
0,04
|
0,03
|
0,01
|
0,00
|
|
2,0
|
0,11
|
0,06
|
0,06
|
0,05
|
0,04
|
0,05
|
0,05
|
0,05
|
0,04
|
0,03
|
0,02
|
0,01
|
0,00
|
Таблица
56
Реактивные давления 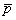
δ = 1,6
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
3,2
|
3,6
|
|
0,0
|
0,10
|
0,09
|
0,09
|
0,09
|
0,10
|
0,13
|
0,14
|
0,16
|
0,18
|
0,16
|
0,12
|
0,07
|
0,04
|
0,04
|
|
0,2
|
0,10
|
0,09
|
0,09
|
0,09
|
0,10
|
0,12
|
0,14
|
0,16
|
0,18
|
0,16
|
0,12
|
0,07
|
0,04
|
0,04
|
|
0,4
|
0,10
|
0,09
|
0,08
|
0,08
|
0,10
|
0,11
|
0,13
|
0,15
|
0,16
|
0,15
|
0,11
|
0,07
|
0,04
|
0,04
|
|
0,6
|
0,09
|
0,08
|
0,07
|
0,07
|
0,08
|
0,10
|
0,12
|
0,13
|
0,14
|
0,13
|
0,09
|
0,06
|
0,04
|
0,04
|
|
0,8
|
0,08
|
0,07
|
0,07
|
0,06
|
0,07
|
0,08
|
0,10
|
0,11
|
0,12
|
0,11
|
0,08
|
0,05
|
0,04
|
0,04
|
|
1,0
|
0,08
|
0,06
|
0,06
|
0,05
|
0,06
|
0,07
|
0,08
|
0,09
|
0,10
|
0,08
|
0,07
|
0,04
|
0,03
|
0,04
|
|
1,2
|
0,07
|
0,06
|
0,05
|
0,05
|
0,05
|
0,05
|
0,06
|
0,07
|
0,07
|
0,06
|
0,05
|
0,03
|
0,03
|
0,03
|
|
1,6
|
0,06
|
0,06
|
0,05
|
0,04
|
0,04
|
0,04
|
0,05
|
0,05
|
0,05
|
0,04
|
0,03
|
0,02
|
0,02
|
0,02
|
|
1,0
|
0,05
|
0,05
|
0,05
|
0,04
|
0,04
|
0,04
|
0,04
|
0,04
|
0,05
|
0,04
|
0,03
|
0,02
|
0,01
|
0,01
|
Таблица 57
Реактивные давления 
δ = 2
|
η
|
ξ
|
|
0,0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,6
|
2,0
|
2,4
|
2,8
|
3,2
|
2,6
|
4,0
|
|
0,0
|
0,07
|
0,07
|
0,07
|
0,06
|
0,07
|
0,08
|
0,09
|
0,11
|
0,15
|
0,17
|
0,15
|
0,11
|
0,07
|
0,95
|
0,03
|
|
0,2
|
0,07
|
0,07
|
0,07
|
0,06
|
0,06
|
0,07
|
0,09
|
0,11
|
0,15
|
0,17
|
0,15
|
0,11
|
0,07
|
0,05
|
0,03
|
|
0,4
|
0,07
|
0,07
|
0,06
|
0,06
|
0,06
|
0,07
|
0,09
|
0,10
|
0,14
|
0,15
|
0,14
|
0,10
|
0,07
|
0,05
|
0,03
|
|
0,6
|
0,06
|
0,06
|
0,06
|
0,06
|
0,06
|
0,07
|
0,08
|
0,09
|
0,12
|
0,13
|
0,12
|
0,09
|
0,06
|
0,04
|
0,03
|
|
0,8
|
0,05
|
0,06
|
0,06
|
0,06
|
0,06
|
0,06
|
0,07
|
0,08
|
0,10
|
0,11
|
0,10
|
0,08
|
0,06
|
0,04
|
0,02
|
|
1,0
|
0,05
|
0,05
|
0,05
|
0,05
|
0,05
|
0,05
|
0,06
|
0,07
|
0,08
|
0,09
|
0,08
|
0,07
|
0,05
|
0,04
|
0,02
|
|
1,2
|
0,04
|
0,04
|
0,04
|
0,05
|
0,05
|
0,05
|
0,05
|
0,06
|
0,07
|
0,07
|
0,07
|
0,06
|
0,01
|
0,03
|
0,02
|
|
2,0
|
0,04
|
0,04
|
0,03
|
0,03
|
0,04
|
0,04
|
0,04
|
0,04
|
0,04
|
0,05
|
0,04
|
0,03
|
0,02
|
0,01
|
0,01
|
Таблица 58
Реактивные
давления 
δ > 2
|
η
|
ξ
|
|
0,0
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,4
|
1,6
|
1,8
|
2,0
|
2,2
|
2,4
|
|
0,0
|
0,192
|
0,162
|
0,136
|
0,114
|
0,094
|
0,077
|
0,063
|
0,051
|
0,041
|
0,033
|
0,026
|
0,020
|
0,015
|
|
0,2
|
0,162
|
0,152
|
0,131
|
0,111
|
0,092
|
0,076
|
0,062
|
0,050
|
0,041
|
0,033
|
0,026
|
0,020
|
0,015
|
|
0,4
|
0,136
|
0,131
|
0,117
|
0,102
|
0,086
|
0,072
|
0,059
|
0,048
|
0,039
|
0,031
|
0,025
|
0,019
|
0,015
|
|
0,6
|
0,114
|
0,111
|
0,102
|
0,089
|
0,077
|
0,065
|
0,055
|
0,045
|
0,037
|
0,029
|
0,023
|
0,018
|
0,014
|
|
0,8
|
0,094
|
0,092
|
0,086
|
0,077
|
0,069
|
0,058
|
0,049
|
0,041
|
0,033
|
0,027
|
0,021
|
0,016
|
0,013
|
|
1,0
|
0,077
|
0,076
|
0,072
|
0,065
|
0,058
|
0,050
|
0,043
|
0,036
|
0,029
|
0,024
|
0,019
|
0,015
|
0,012
|
|
1,2
|
0,063
|
0,062
|
0,059
|
0,055
|
0,049
|
0,043
|
0,037
|
0,031
|
0,026
|
0,021
|
0,016
|
0,013
|
0,010
|
|
1,4
|
0,051
|
0,050
|
0,048
|
0,045
|
0,041
|
0,036
|
0,031
|
0,027
|
0,022
|
0,017
|
0,014
|
0,012
|
0,009
|
|
1,6
|
0,041
|
0,041
|
0,039
|
0,037
|
0,033
|
0,029
|
0,026
|
0,022
|
0,018
|
0,015
|
0,012
|
0,010
|
0,008
|
|
1,8
|
0,033
|
0,033
|
0,031
|
0,029
|
0,027
|
0,024
|
0,021
|
0,017
|
0,015
|
0,013
|
0,010
|
0,009
|
0,007
|
|
2,0
|
0,026
|
0,026
|
0,025
|
0,033
|
0,021
|
0,019
|
0,016
|
0,014
|
0,012
|
0,010
|
0,009
|
0,007
|
0,006
|
|
2,2
|
0,020
|
0,020
|
0,019
|
0,018
|
0,016
|
0,015
|
0,013
|
0,012
|
0,010
|
0,009
|
0,007
|
0,006
|
0,004
|
|
2,4
|
0,015
|
0,015
|
0,015
|
0,014
|
0,013
|
0,012
|
0,010
|
0,009
|
0,008
|
0,007
|
0,006
|
0,004
|
0,003
|
|
2,6
|
0,012
|
0,012
|
0,012
|
0,010
|
0,010
|
0,009
|
0,008
|
0,005
|
0,005
|
0,005
|
0,004
|
0,003
|
0,002
|
|
2,8
|
0,009
|
0,009
|
0,009
|
0,008
|
0,008
|
0,007
|
0,007
|
0,006
|
0,005
|
0,004
|
0,003
|
0,002
|
0,002
|
Продолжение
табл. 58
Реактивные давления 
δ > 2
|
η
|
ξ
|
|
0,0
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
1,4
|
1,6
|
1,8
|
2,0
|
2,2
|
2,4
|
|
3,0
|
0,007
|
0,007
|
0,007
|
0,006
|
0,006
|
0,005
|
0,005
|
0,004
|
0,003
|
0,002
|
0,002
|
0,002
|
0,002
|
|
3,2
|
0,005
|
0,005
|
0,005
|
0,004
|
0,004
|
0,003
|
0,003
|
0,002
|
0,002
|
0,002
|
0,002
|
0,002
|
0,001
|
|
3,4
|
0,003
|
0,003
|
0,003
|
0,002
|
0,002
|
0,002
|
0,002
|
0,002
|
0,002
|
0,002
|
0,002
|
0,001
|
|
|
3,6
|
0,002
|
0,002
|
0,002
|
0,002
|
0,002
|
0,002
|
0,002
|
0,002
|
0,002
|
0,001
|
0,000
|
|
|
|
3,8
|
0,002
|
0,002
|
0,002
|
0,002
|
0,002
|
0,002
|
0,001
|
0,001
|
0,000
|
|
|
|
|
|
4,0
|
0,001
|
0,001
|
0,001
|
0,001
|
0,001
|
|
|
|
|
|
|
|
|
Продолжение
табл. 58
Реактивные давления 
δ > 2
|
η
|
ξ
|
|
2,6
|
2,8
|
3,0
|
3,2
|
3,4
|
3,6
|
3,8
|
4,0
|
|
0,0
|
0,012
|
0,009
|
0,007
|
0,005
|
0,003
|
0,002
|
0,002
|
0,001
|
|
0,2
|
0,012
|
0,009
|
0,007
|
0,005
|
0,003
|
0,002
|
0,002
|
0,001
|
|
0,4
|
0,012
|
0,009
|
0,007
|
0,005
|
0,003
|
0,002
|
0,002
|
0,001
|
|
0,6
|
0,010
|
0,008
|
0,006
|
0,004
|
0,002
|
0,002
|
0,002
|
0,001
|
|
0,8
|
0,010
|
0,008
|
0,006
|
0,004
|
0,002
|
0,002
|
0,002
|
|
|
1,0
|
0,009
|
0,007
|
0,006
|
0,003
|
0,002
|
0,002
|
0,002
|
|
|
1,2
|
0,008
|
0,007
|
0,005
|
0,003
|
0,002
|
0,002
|
0,001
|
|
|
1,4
|
0,008
|
0,006
|
0,004
|
0,002
|
0,002
|
0,002
|
0,001
|
|
|
1,6
|
0,007
|
0,005
|
0,003
|
0,002
|
0,002
|
0,002
|
|
|
|
1,8
|
0,005
|
0,004
|
0,002
|
0,002
|
0,002
|
0,001
|
|
|
|
2,0
|
0,004
|
0,003
|
0,002
|
0,002
|
0,002
|
|
|
|
|
2,2
|
0,003
|
0,002
|
0,002
|
0,002
|
0,001
|
|
|
|
|
2,4
|
0,002
|
0,002
|
0,002
|
0,001
|
|
|
|
|
|
2,6
|
0,002
|
0,002
|
0,001
|
|
|
|
|
|

Рис.
9. Схема плитного фундамента для определения переменного коэффициента жесткости
основания
q1, f1 - номера сторон основной сетки; q0, f0 - номера сторон общей сетки; x0,
y0, x1, y1, x2, y2 - осн. координат; ∆x1,
∆y1 - длины сторон общей сетки; Скв. 1 - Скв. 5 -
геологические скважины
Таблица 59
|
Номер
точки фундамента i
|
Коэффициенты
ki при n = l/b
|
|
1
|
1,4
|
1,7
|
2,4
|
3,2
|
5
|
|
0
|
1,122
|
1,316
|
1,467
|
1,644
|
1,783
|
2,104
|
|
1
|
0,766
|
0,930
|
1,064
|
1,226
|
1,358
|
1,669
|
|
2
|
0,766
|
0,870
|
0,949
|
1,039
|
1,110
|
1,272
|
|
3
|
0,561
|
0,658
|
0,734
|
0,822
|
0,891
|
0,052
|
4.8. Значения переменного коэффициента жесткости в узлах q0f0 общей сетки (рис. 9.), наносимой на план фундамента с
шагом меньшим, чем шаг основной сетки qf, определяют по линейной интерполяции.
4.9. Рекомендациями пп.
4.5 - 4.8 можно пользоваться для вычисления переменного коэффициента
жесткости основания плитного фундамента произвольной ортогональной формы, если
условно разрезать фундамент на отдельные прямоугольные фундаменты или фундамент произвольной
ортогональной формы привести к прямоугольному с сохранением основных габаритов,
взаимного расположения колонн и длин консольных участков. При этом произвольное
положение колонн приводят к прямоугольной сетке путем введения нулевых нагрузок
на колонны и нагрузки от стены здания заменяют нагрузкой по отдельным
прямоугольным участкам.
4.10. При вычислении переменного коэффициента жесткости
основания достаточно точно учитывают влияние жесткости плитного фундамента,
применяя итерационный метод. В соответствии с этим методом на первом шаге
вычислений предусматривают нахождение осадок основания от равномерно
распределенного среднего давления и определение величин переменного
коэффициента жесткости по формуле (44). Затем
выполняют расчет фундамента с вычисленными значениями коэффициента жесткости
основания. На втором шаге расчета выполняют те же вычисления, что и на первом
шаге, но от неравномерно распределенной нагрузки, равной реактивному давлению,
найденному в результате расчета фундамента. Вычисления заканчивают тогда, когда
соответствующие величины переменного коэффициента жесткости основания,
полученные по двум последним итерациям, отличаются не более чем на 5-10 %.
4.11. Переменный коэффициент жесткости основания вычисляют
на ЭВМ по программе «ПРОЛОГ-4» на первом этапе расчета, предусмотренного п.
4.10. Основные характеристики программы «ПРОЛОГ-4» даны в прил.
1.
Пример вычисления на ЭВМ по программе «ЖОК»
переменного коэффициента жесткости основания
Требуется определить величины переменного
коэффициента жесткости неоднородного в плане и по глубине основания с учетом
дополнительных осадок основания за счет нагрузки от соседнего здания и с
приближенной оценкой влияния жесткости плитного фундамента на осадки основания
н реактивные давления.
План плитного фундамента каркасного
здания приведен на рис.
3 и 9.
Вычисления проводят на ЭВМ по программе
«ЖОК». Исходные данные к расчету составляют с использованием результатов
расчета деформаций основания и вычисления
предварительных размеров плитного
фундамента, выполненных на ЭВМ соответственно по программам «GEST-82» и «РАПОРТ».
Для вычисления значений переменного
коэффициента жесткости основания на ЭВМ по программе «ЖОК» задают следующие
исходные данные: количество рядов колонн n = 4 и m = 6
по осям x1,
y1;
количество узлов основной сетки n1 = 3 и m1 = 5 и количество узлов
общей сетки n0 = 5 и m0 = 9 по осям x2, y2, длина
фундамента l = 33 м; ширина
b =
22 м; осредненный приведенный модуль деформации основания с корректирующим
коэффициентом  = 119760 кПа; осредненный коэффициент
бокового расширения грунта μср
= 0,329; упругая характеристика фундамента L = l,88 м; длины
консолей l1 = l2 = 1,5 м, l3 = l4 = 2,0 м; координаты центров колонн в системе
координат x1, y1, м (табл. 60); вертикальные нагрузки на колонны, кН
(табл. 61); полные осадки Sqf основания в узлах qf основной сетки, найденные по напряжениям послойным
суммированием осадок, с учетом дополнительных напряжений от нагрузки,
передаваемой соседним зданием, м (табл. 62). = 119760 кПа; осредненный коэффициент
бокового расширения грунта μср
= 0,329; упругая характеристика фундамента L = l,88 м; длины
консолей l1 = l2 = 1,5 м, l3 = l4 = 2,0 м; координаты центров колонн в системе
координат x1, y1, м (табл. 60); вертикальные нагрузки на колонны, кН
(табл. 61); полные осадки Sqf основания в узлах qf основной сетки, найденные по напряжениям послойным
суммированием осадок, с учетом дополнительных напряжений от нагрузки,
передаваемой соседним зданием, м (табл. 62).
Таблица
60
|
Номера
рядов колонн i
|
Координаты
центров колонн ряда j
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
x1
|
y2
|
x1
|
y2
|
x1
|
y2
|
x1
|
y2
|
x1
|
y2
|
x1
|
y2
|
|
1
|
0
|
0
|
6
|
0
|
12
|
0
|
18
|
0
|
24
|
0
|
30
|
0
|
|
2
|
0
|
6
|
6
|
6
|
12
|
6
|
18
|
6
|
24
|
6
|
30
|
6
|
|
3
|
0
|
12
|
6
|
12
|
12
|
12
|
18
|
12
|
24
|
12
|
30
|
12
|
|
4
|
0
|
18
|
6
|
18
|
12
|
16
|
18
|
18
|
24
|
18
|
30
|
18
|
Таблица
61
|
Номера
рядов колонн i
|
Вертикальные
нагрузки на колонны ряда j
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
3500
|
4500
|
4500
|
4500
|
4500
|
3500
|
|
2
|
3500
|
6500
|
6500
|
6500
|
6500
|
3500
|
|
3
|
3500
|
6500
|
6500
|
6500
|
6500
|
3500
|
|
4
|
3500
|
4500
|
4500
|
4500
|
4500
|
3500
|
Таблица
62
|
Номера
сторон сетки q
|
Осадки
узлов по стороне f основной
сетки
|
|
1
|
2
|
3
|
4
|
5
|
|
1
2
3
|
0,0113
0,0196
0,0109
|
0,0167
0,0375
0,0185
|
0,0178
0,0375
0,0182
|
0,0153
0,0332
0,0187
|
0,0083
0,0172
0,0235
|
В результате расчета найдены и
выданы на АЦПУ координаты узлов q0f0 общей сетки
в системе координат х2 у2, м (табл. 63) и
коэффициенты жесткости основания kqf в узлах общей сетки, кН/м3 (табл. 64).
Таблица 63
|
Номера
сторон сетки q0
|
Координаты
узлов по стороне f0
общей сетки
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
x2
|
y2
|
x2
|
y2
|
x2
|
y2
|
x2
|
y2
|
x2
|
y2
|
x2
|
y2
|
x2
|
y2
|
x2
|
y2
|
x2
|
y2
|
|
1
|
0
|
0
|
4,12
|
0
|
8,25
|
0
|
12,37
|
0
|
16,5
|
0
|
20,62
|
0
|
24,75
|
0
|
28,87
|
0
|
33
|
0
|
|
2
|
0
|
5,5
|
4,12
|
|
8,25
|
0,5
|
12,37
|
5,5
|
16,5
|
0,5
|
20,62
|
5,5
|
24,75
|
5,5
|
28,87
|
5,5
|
33
|
5,5
|
|
3
|
0
|
11
|
4,12
|
|
8,225
|
11
|
12,37
|
11
|
16,5
|
11
|
20,62
|
И
|
24,75
|
11
|
28,87
|
11
|
33
|
11
|
|
4
|
0
|
16,5
|
4,12
|
|
8,25
|
16,5
|
12,37
|
16,5
|
16,5
|
16
5
|
20,62
|
16,5
|
24,75
|
16,5
|
28,87
|
16,5
|
33
|
16,5
|
|
5
|
|
22
|
4,12
|
|
8,25
|
22
|
12,37
|
22
|
16,5
|
22
|
20,62
|
22
|
24,75
|
22
|
28,87
|
22
|
33
|
22
|
Таблица 64
|
Номера
сторон сетки q0
|
Коэффициенты
жесткости основания в узлах по стороне f0 общей
сетки
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
1
|
166334,2
|
126831,4
|
87328,6
|
94422,9
|
101517,1
|
98418,3
|
95319,5
|
160887,3
|
226455,2
|
|
2
|
149653
|
98763,8
|
47874,6
|
51120,1
|
54365,6
|
53390,4
|
52415,3
|
120702,9
|
188990,5
|
|
3
|
132971,8
|
70696,2
|
8420,6
|
7817,4
|
7214,4
|
8362,7
|
9511,3
|
80518,6
|
151525,9
|
|
4
|
152704,9
|
98165,6
|
43626,2
|
48438,1
|
53250
|
48500
|
43749,9
|
79752
|
115753,9
|
|
5
|
172438,1
|
125635,0
|
78831,8
|
89058,9
|
99286
|
88637,3
|
77988,7
|
78985,4
|
79982
|
В дальнейшем при расчете
плитного фундамента коэффициент жесткости основания в узлах, расположенных по
контуру фундамента, принимают равным его значениям в следующем параллельном
ряде узлов, так как значения коэффициента жесткости, вычисленные для контурных
узлов, резко убывают на малом расстоянии от контура фундамента.
5. СТАТИЧЕСКИЕ РАСЧЕТЫ ПЛИТНЫХ
ФУНДАМЕНТОВ
5.1. Статические расчеты плитных фундаментов, как правило,
выполняют на ЭВМ по рекомендуемым в настоящем разделе и в прил.
1 программам с целью определения усилий в фундаменте, перемещений
фундамента и реактивных давлений основания, необходимых для проверки
допустимости совместных деформаций основания, фундамента и конструкций верхнего
строения, последующих или параллельных расчетов сечений фундамента, подбора
арматуры (или проверки принятых сечений фундамента и армирования) и проверки
ширины раскрытия трещин.
5.2. При разработке программ для расчета плитных
фундаментов на ЭВМ рекомендуется применять расчетную схему основания,
подчиняющегося гипотезе переменного коэффициента жесткости, наиболее удобную
для математической реализации, либо в виде линейно-деформируемого слоя в
зависимости от сложности поставленной задачи и однородности основания.
Величины переменного коэффициента
жесткости в соответствии с рекомендациями разд.
4 находят по ожидаемым осадкам основания, напряжения в котором определяются
по зависимостям для линейно-деформируемого слоя.
5.3. Для расчета плитных фундаментов в зависимости от
сложности решаемых задач применяют удобные для реализации на ЭВМ численные
методы (конечно-разностный, вариационно-разностный и конечных элементов) с
использованием как непрерывных (континуальных), так и дискретных расчетных схем
фундамента.
5.4. Усилия в плитном фундаменте, а также деформации
основания при строгой постановке задачи должны определяться расчетом из условия
совместной работы надфундаментной конструкции, фундамента и основания с учетом
неоднородности основания по глубине и в плане, распределяющей способности
основания, воздействия соседних зданий и сооружений, а также неупругих
деформаций грунта, бетона и арматуры фундамента, материала элементов
надфундаментных конструкций и наличия трещин в фундаменте.
Для упрощения такого расчета, чрезвычайно
сложного и трудоемкого даже при использовании ЭВМ, в зависимости от сложности
практических задач можно выполнить раздельный расчет основания, плитного
фундамента на сжимаемом основании и надфундаментных конструкций, для которого в
необходимых случаях применяют метод итераций, а также можно использовать
приближенные приемы учета неупругих деформаций основания, плитного фундамента и
элементов надфундаментных конструкций либо выполнить расчет фундамента в
предположении линейно-упругого деформирования материала фундамента, элементов
надфундаментных конструкций и грунтов основания (в так называемой линейной
постановке задачи) с использованием принципа независимости действия сил, а
подбор арматуры и проверку прочности сечения фундамента производить на
найденные усилия в соответствии с указаниями главы СНиП на проектирование бетонных
и железобетонных конструкций.
5.5. Возможности выбираемого метода статического расчета
плитного фундамента оценивают с помощью следующих расчетных характеристик
фундамента:
показателя гибкости фундамента:
а) прямоугольного
|
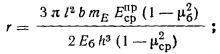
|
(49)
|
б) круглого
|
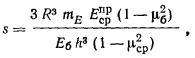
|
(50)
|
где
R - радиус фундамента;
Еб - начальный модуль упругости бетона при растяжении и
сжатии;
μб - коэффициент бокового расширения бетона;
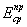 - осредненный приведенный модуль деформации
основания, определяемый по указаниям разд. 2; - осредненный приведенный модуль деформации
основания, определяемый по указаниям разд. 2;
μср - осредненный коэффициент бокового расширения
основания, вычисляемый по рекомендациям разд. 2;
mЕ -
корректирующий коэффициент, определяемый по п. 3.11;
h - толщина;
l -
длина и b - ширина прямоугольного
фундамента или условная ширина фундамента сложной формы в плане, эквивалентного
по площади прямоугольному длиной l;
показателя гибкости прямоугольного
фундамента в направлении длины
|

|
(51)
|
показателя гибкости прямоугольного
фундамента в направление ширины
|

|
(52)
|
упругой характеристики фундамента,
определяемой по формуле (37).
Метод расчета и программу
для ЭВМ выбирают, руководствуясь следующей классификацией плитных фундаментов:
а) по форме в плане:
прямоугольные;
произвольной ортогональной либо
полигональной формы;
круглые;
кольцевые;
б) по форме сечения:
постоянной толщины (плоские);
переменной толщины (с монолитными
подколонниками и ступенчато-переменной толщины);
ребристые (с ребрами в одном или в двух
направлениях);
коробчатые;
в) в зависимости от типа
надфундаментного строения различают плитные фундаменты, работающие совместно:
со связевым каркасом;
рамным каркасом;
рамно-связевым каркасом;
несущими стенами;
верхним строением сооружения башенного
типа (силосный корпус, дымовая труба и т.п.), непосредственно опирающимся на
фундамент или через колонны;
г) по соотношению сторон
прямоугольной опорной площади:
плиты, если отношение длины
фундамента к ширине l/b ≤ 5;
балочные плиты, если l/b > 5 и показатель гибкости в направлении ширины tп > 1,5*;
*Если
l/b > 5 и показатель гибкости в
направлении ширины tп ≤ 1,5, то
фундамент рассчитывают как балку на упругом основании.
д) по отношению толщины к
ширине прямоугольного либо к диаметру круглого или к стороне квадратного
плитного фундамента эквивалентного по площади фундаменту произвольной формы в
плане*:
тонкие, если h/b ≤ 0,1;
средней толщины, если 0,1 < h/b ≥
0,25;
толстые, если h/b < 0,25;
*В
настоящем Руководстве рассматриваются способы расчета плитных фундаментов,
относящихся к категории тонких и средней толщины.
е) по расчетным категориям*:
*Перечисленные
в п.
5.6 «г», «д» расчетные категории плитных фундаментов продиктованы
особенностями статической работы, учитываемыми при расчете.
жесткие, если показатель гибкости
|
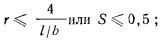
|
(53)
|
конечной жесткости, если
|

|
(54)
|
гибкие или большой протяженности, если
|
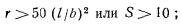
|
(55)
|
большой протяженности только в
направлении длины, если r > 50 (b/l) и показатель гибкости в направлении ширины tп > 1,5.
5.7. Плитные фундаменты
прямоугольной, сложной ортогональной, полигональной и круглой формы в плане,
для которых разработаны методы и программы статического расчета на ЭВМ, с
расчетными схемами, показанными на рис. 10 - 16 (применительно к прямоугольным плитным фундаментам
каркасных зданий), условно разделены на четыре группы:
1а - плиты, рассчитываемые методами
технической теории расчета тонких и средней толщины изотропных плит на упругом
основании с использованием расчетных схем основания, рекомендуемых в разд. 1, и 1б
- плиты на упругом основании, рассчитываемые по технической теории тонких
анизотропных плит с учетом особенностей деформирования железобетона с
использованием метода переменных параметров упругости в сочетании с шаговым
нагружением плиты при расчетной схеме основания, характеризуемой переменным
коэффициентом жесткости, определяемым по разд.
4 (рис.
10 - 13);
2 - плоские и ребристые плиты,
рассчитываемые по дискретной схеме в виде системы ортогональных перекрестных
балок, имеющих непрерывный контакт с основанием (рис.
14);
3 - плиты, заменяемые
дискретной системой перекрестных балок-полос на дискретных упругих опорах,
располагаемых в местах пересечения осей балок (рис.
15 и 16).
Нагрузка от колонн сосредоточенная. Балки-полосы рассчитывают по универсальным
программам расчета пространственных стержневых систем;
4 - плиты прямоугольной и
сложной формы в плане, рассчитываемые с использованием приближенных расчетных
схем (замена плиты балкой, вырезание полос, расчленение плиты на бесконечную,
полубесконечную и четвертьбесконечную плиты и др.).
5.8. Для статического расчета плитного фундамента на ЭВМ выполняют
следующую подготовительную работу по рекомендациям разд. 1 - 4 вручную либо с
помощью ЭВМ по программам типа «GEST-82», «ЖОК»
и «РАПОРТ»: определяют схемы и величины расчетных нагрузок на плитный
фундамент; выбирают расчетную схему и параметры основания; производят расчет
деформаций основания; принимают расчетную
схему основания для совместного расчета основания и плитного фундамента;
находят предварительные размеры фундамента по условию минимального объема бетона;
определяют расчетную категорию фундамента; выбирают расчетную схему фундамента,
метод статического расчета, а также программу для расчета плитного фундамента
на ЭВМ; подготавливают исходные данные для расчета фундамента на ЭВМ в
соответствии с инструкцией к выбранной программе.

Рис.
10. Расчетная схема плиты постоянной толщины, нагруженной вертикальными
нагрузками, равномерно распределенными по отдельным прямоугольным площадкам

Рис.
11. Расчетная схема плиты ступенчато-переменной толщины, нагруженной
вертикальными нагрузками, равномерно распределенными по отдельным прямоугольным
площадкам

Рис.
12 Расчетная схема плиты постоянной толщины с участками большой жесткости в
местах опирания диафрагм

Рис.
13. Расчетная схема плиты постоянной толщины, нагруженной вертикальными
нагрузками, равномерно распределенными по отдельным прямоугольным площадкам с
участками, соединенными с жестким верхним строением с помощью податливых колонн
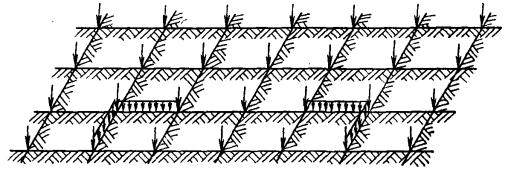
Рис.
14. Дискретная расчетная схема прямоугольной плиты в виде системы перекрестных
балок, имеющих непрерывный контакт с основанием

Рис.
15. Расчетная схема прямоугольной плиты в виде системы перекрестных балок на
дискретных упругих опорах

Рис.
16. Упрощенная расчетная схема совместного расчета плиты и связевого каркаса (стержневая
пространственная система)
5.9. Программы для статического расчета плитных
фундаментов выбирают в зависимости от типа имеющейся ЭВМ, формы в плане и расчетной категории плитного фундамента,
конструктивной схемы надфундаментного строения и необходимости оценки влияния
на статическую работу плитного фундамента следующих факторов: нелинейных
деформаций грунтов основания, нелинейной работы железобетона и
трещинообразования в бетоне плитного фундамента и надфундаментных конструкций,
возникновения реактивных касательных напряжений по подошве фундамента и других
факторов.
При оценке возможностей программы
учитывают особенности реализуемого программой метода расчета плитного
фундамента, принятые расчетные схемы и допущения, а также получаемые
результаты.
5.10. Указания
раздела относятся к статическим расчетам плитных фундаментов с учетом
совместной работы основания, плиты и надфундаментного строения при следующих
предпосылках (рис. 17):
плита ортотропная произвольной
конфигурации в плане с ортогональными краями, постоянной или переменной
толщины, либо с ребрами, диафрагмами, стенами как отдельно стоящими, так и
соединенными жесткими связями, с жесткими вставками, подколонниками,
отверстиями, имеющими ортогональный контур;
срединная поверхность плиты плоская;
деформации плиты описываются уравнениями
технической теории тонких жестких пластин;
вертикальные перемещения точек плиты и
основания одинаковы;
силы трения между плитой и основанием
отсутствуют;
материалы плиты и основания
линейно-упругие;
плита опирается на сжимаемое основание
либо на сжимаемое основание и жесткие опоры одновременно;
основание плиты однородное и неоднородное
по сжимаемости в плане, характеризуется переменным коэффициентом жесткости,
определяемым по указаниям разд.
4;
нагрузки вертикальные, произвольно
расположенные;
моментные нагрузки от жестких диафрагм
заменяются парами вертикальных сил.

Рис. 17. Варианты нагрузок, типы и параметры плитного
фундамента и оснований при расчетах по программе ПОРТИК
5.11. Расчет производится вариационно-разностным методом, в
соответствии с которым величину потенциальной энергии системы определяют из
соотношения
где
Uп -
потенциальная энергия деформации плиты;
Uо -
потенциальная энергия деформации основания;
П -
работа внешних сил (изменение потенциала внешних сил).
Потенциальная энергия деформации плиты,
энергия деформации основания и работа внешних сил находятся из выражений:
|

|
(57)
|
где
F - площадь плиты;
р - реактивное
давление основания;
q - интенсивность внешней нагрузки;
w - прогибы, перемещения плиты;
Мх, Му - изгибающие моменты;
Мху - крутящий момент.
С учетом ортотропности плиты моменты
равны:
где
А, В, С, D - жесткости плиты;
х, λ, ω - кривизны и кручение,
определяемые соотношениями:
|

|
(59)
|
где
Е и μ -
упругие характеристики плиты: модуль упругости и коэффициент Пуассона;
hо - основная
толщина плиты;
hx и hу - толщины плиты в точках, где она отличается от
основной и где имеются подколонники, пилоны, ребра, стены, диафрагмы и другие
элементы, изменяющие жесткость плиты и оказывающие влияние на ее деформацию.
При этом считается, что ребра, стены и диафрагмы, имеющие незначительную
толщину, оказывают влияние на деформацию плиты только в направлении своей
продольной в плане оси.
При решении задачи вариационно-разностным методом на
плиту наносится регулярная прямоугольная сетка. Кривизны и кручения заменяются
разностными отношениями:
|

|
(60)
|
Потенциальная энергия системы
записывается как функция перемещений узлов плиты
|
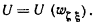
|
(61)
|
Используя принцип Лагранжа, разрешающую
систему линейных уравнений получают путем дифференцирования выражения
потенциальной энергии по прогибам в каждом узле конечно-разностной сетки,
нанесенной на плиту,

|
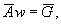
|
(62)
|
Система разрешающих уравнений имеет вид
где
 - матрица системы; - матрица системы;
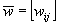 - вектор прогибов; - вектор прогибов;
 -вектор нагрузок -вектор нагрузок
Элементы матрицы определяются путем
набора соответствующих операторов, приведенных в табл. 65. Порядок набора
операторов зависит от положения на плите узла сетки, для которого формируется
уравнение (рис.
18).
Таблица 65
Элементарные
операторы для формирования уравнений (62).
|
Тип
элементарного оператора
|
Элементарный
оператор
|
|
1. Изгибный
для внутреннего центрального узла
|

|
|
2. Изгибный
для внутреннего верхнего узла
|
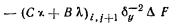
|
|
3. Изгибный
для внутреннего узла справа
|

|
|
4. Изгибный
для внутреннего нижнего узла
|

|
|
5. Изгибный
для внутреннего узла слева
|

|
|
6. Крутильный
для верхней ячейки справа
|
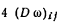
|
|
7. Крутильный
для нижней ячейки справа
|

|
|
8.
Крутильный для нижней ячейки слева
|

|
|
9. Крутильный
для верхней ячейки слева
|

|
|
10. Изгибный
для центрального узла на горизонтальном краю
|

|
|
11. Изгибный
для узла справа на горизонтальном краю
|

|
|
12. Изгибный
для узла слева на горизонтальном краю
|
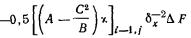
|
|
13. Изгибный
для центрального узла на вертикальном краю
|

|
|
14. Изгибный
для верхнего узла на вертикальном краю
|

|
|
15. Изгибный
для нижнего узла на вертикальном краю
|

|
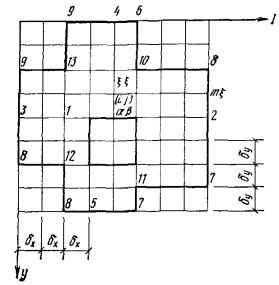

Рис. 18. Типы узлов конечно-разностной
метки для плит произвольной формы в плане
После решения системы линейных
алгебраических уравнений получают величины прогибов для всех узлов сетки.
Для определения величин изгибающих и
крутящих моментов, действующих в сечениях плиты, используют выражения (58).
Реакции основания определяют по формуле
где
pi - реакция основания для i-го узла сетки;
ki - коэффициент жесткости основания в i-ом узле;
wi - прогиб плиты в i-ом узле.
5.12. При подготовке расчетной схемы перемещения плиты в
точках расположения жестких опор принимаются равными нулю:
wi
= 0.
При известной величине осадки свай в
точках расположения свай задается коэффициент жесткости основания, определяемый
по формуле
|

|
(64)
|
где
q - средняя величина нагрузки на плиту;
si - осадка опоры.
5.13. Для расчета плит с учетом влияния жесткости
надфундаментного строения следует использовать метод сил.
При этом принимают следующие предпосылки:
надфундаментное строение состоит из
системы абсолютно жестких в своей плоскости диафрагм, расположенных параллельно
координатам;
все диафрагмы связаны между собой
абсолютно жесткими в горизонтальной плоскости связями, роль которых в реальной
конструкции играют диски перекрытий;
от диафрагм на плиту передаются только
вертикальные усилия, равные соответствующей внешней нагрузке, и моменты,
величина которых определяется в результате расчета;
углы наклона диафрагм одного направления
одинаковы, закручивание здания при этом не учитывается;
влияние горизонтальных усилий
взаимодействия между плитой и диафрагмой не учитывается;
колонны передают на плиту только
вертикальную нагрузку;
жесткость колонн не учитывается.
Окончательные результаты расчета плиты
получаются суммированием величин, получаемых от действия внешних нагрузок и от
моментов взаимодействия плиты с диафрагмами.

Рис. 19. Расчетная схема плиты при учете
совместной работы с надфундаментным строением
5.14. Для
расчета плиты любой формы в плане следует принимать прямоугольную в плане разностную
сетку, в которую вписывают рассчитываемую плиту. Сетка может быть как с
квадратными, так и с прямоугольными ячейками. Шаг сетки в одном направлении
принимается одинаковым. Число узлов сетки должно быть минимальным, но
достаточным для характеристики деформации плиты и внутренних усилий,
возникающих в ее сечениях. Оптимальным считается шаг, при котором размеры
ячейки сетки соответствуют размерам площади на срединной поверхности плиты,
воспринимающей нагрузку от несущего элемента верхнего строения.
Приближенно величину шага сетки
определяют по формуле
δ = a + h,
где
δ - шаг сетки;
а - минимальная ширина элемента, передающего нагрузку на
плиту;
h - толщина плиты.
5.15. Точки приложения сосредоточенных нагрузок и центры
тяжести площадок нагружения нужно совмещать с ближайшими узлами сетки.
5.16.
Оси
элементов надфундаментного строения (диафрагм, стен) должны совпадать с линиями сетки, для чего допускается некоторое
смещение осей элементов от проектного положения.
Толщина стены приближенно принимается
кратной шагу сетки. В этом случае ось стены или диафрагмы может не совпадать с
линией сетки (рис. 20). Диафрагмы, связанные между собой, не должны иметь
толщину больше, чем величина 1-го шага сетки.
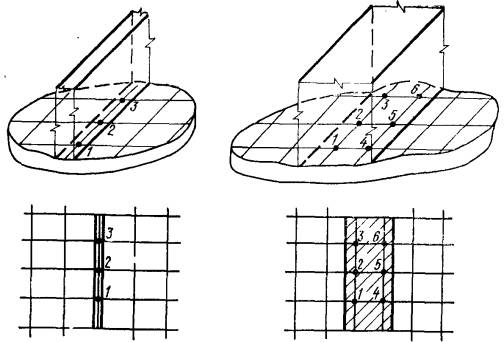
Рис.
20. Схематизация диафрагм при расчете плиты по программе ПОРТИК
Пример. Рассмотрим фундаментную плиту произвольной
ортогональной конфигурации (рис. 21). Размеры прямоугольника, в который
вписывается данная плита, равны 39 × 24 м. Основная толщина плиты 1,5 м.
Ребра жесткости имеют высоту 1 м. Марка бетона 200. Модуль упругости бетона Е = 2,4·107 кПа. Коэффициент
Пуассона μ = 0,2. Плита
загружена системой сосредоточенных сил, приложенных в узлах сетки, принятой для
расчета. Суммарная нагрузка на плиту 307,8 МН. Шаг сетки в обоих направлениях
равен 1,5 м. В одном из расчетов в качестве основания принята модель с
переменным коэффициентом жесткости. Схема распределения коэффициентов
жесткости, МН/м3, по площади плиты и их величины показана на рис.
22. В другом расчете основание было однородным с коэффициентом постели, равным
1,75 МН/м3. Результаты обоих расчетов приведены на рис. 23. Эпюры
изгибающих моментов показаны для сечений 1-1 и 2-2.
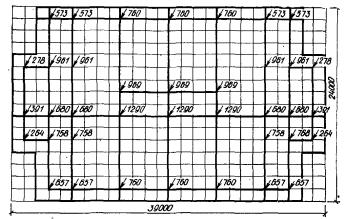
Рис.
21. Схема плитного фундамента, рассчитанного на однородном н неоднородном
основании

Рис.
22. Схема распределения коэффициентов жесткости основания в плане плиты

Рис. 23. Сопоставление результатов расчетов плиты на неоднородном и
однородном основаниях
1 -
неоднородное основание; 2 - однородное основание
5.17. Рекомендации раздела
относятся к расчету прямоугольных железобетонных
фундаментов ответственных сооружений, для проектирования которых
требуется более строгая оценка конструкции по предельным состояниям второй
группы.
5.18. Расчет плиты выполняется с учетом особенностей
деформирования железобетона методом переменных параметров упругости в сочетании
с шаговым увеличением нагрузки путем сведения нелинейной задачи к многократному
линейному расчету анизотропной плиты переменной жесткости. При этом анизотропия
железобетона плиты определяется направлением трещин и расположением арматуры.
Решение задачи получается численными
методами с использованием в качестве физической основы теории деформирования
железобетона с трещинами*.
*Карпенко
Н.И. Теория деформирования железобетона с трещинами. М., Стройиздат, 1976.
5.19. Жесткости плиты, соответствующие заданным кривизнам,
должны вычисляться с учетом истории нагружения плиты посредством процесса
«микроитераций» в соответствии с указаниями п.
5.24.
5.20. При расчете плиты принимаются следующие допущения:
плита относится к расчетной
категории тонких жестких плит;
силы трения между плитой и
основанием не учитывают;
срединную поверхность плиты в
случае переменной толщины приближенно принимают плоской;
нагружение считают однократным
при пропорциональном росте сил;
связи между основанием и
плитой принимают двусторонними, но возможен и учет односторонности этих связей;
влияние ветровых нагрузок
учитывается соответствующим перераспределением вертикальных сил.
5.21. Основание плиты характеризуется переменным
коэффициентом жесткости, определяемым по указаниям разд.
4.
5.22. В качестве исходных данных для расчета должны быть
заданы: геометрия плиты (размеры в плане и толщина плиты h в любой точке); марка бетона R, прочность на сжатие RпрII и на
растяжение RрII; начальный модуль
упругости бетона Еб;
площадь верхней и нижней арматуры, которая предполагается параллельной
осям X и У (краям плиты)
и обозначается соответственно f'ax, f'ay, fаx, fay;
расчетные высоты по нижней и верхней
арматурам h0 и h'0, причем

предел упругости σуп; предел текучести σт; предел прочности σв; модуль упругости Еа н вид арматурной стали; действующая
на плиту вертикальная нагрузка; характеризующее основание распределение в плане
переменного коэффициента жесткости.
a Наиболее рациональным численным методом расчета
анизотропной плиты переменной жесткости является вариационно-разностный.
Использование разностной сетки сводит расчет континуальной системы к
рассмотрению дискретной схемы и позволяет анализировать стадии работы плиты в
каждом узле сетки.
Разрешающие уравнения задачи расчета
плиты получаются минимизацией потенциальной энергии системы. Варьируемыми
параметрами являются перемещения плиты в узлах разностной сетки (рис.
18)
Работа внешних сил находится по формуле
|

|
(66)
|
где
q - интенсивность распределенной нагрузки.
При использовании метода сеток работа
внешних сил равна:
|
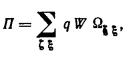
|
(67)
|
где
Ωζξ - сеточная площадь, соответствующая ζξ-му узлу.
Производная этого слагаемого
потенциальной энергии по перемещению Wij равна:
Потенциальная энергия деформации
основания определяется выражением
|
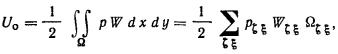
|
(69)
|
где
Pζξ -
интенсивность реактивного давления в ζξ -ом узле.
Для основания, описываемого коэффициентом
жесткости k, реактивное давление определяют по формуле

В результате дифференцирования по Wij получают
В выражениях (67) - (70) сеточная площадь
Ω для внутренних узлов равна δx δy; для
контурных - 1/2 δx δy, для угловых - 1/4 δx δy, где
δх и δу - шаг разностной сетки
соответственно по X и Y.
Потенциальную энергию деформации плиты
определяют по формуле
|
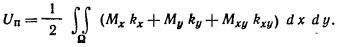
|
(71)
|
В этом выражении используются линейные
геометрические и физические соотношения: крутизны
|

|
(72)
|
изгибающие моменты
крутящий момент
|
Mxy = Ekx + Fky
+ Dkxy.
|
(74)
|
В соотношениях (73) и (74) А, В, С, D, E, F - коэффициенты жесткости, учитывающие анизотропию
плиты.
Подстановкой выражений (73) и (74) в
зависимость (71) находится потенциальная энергия деформации плиты
|
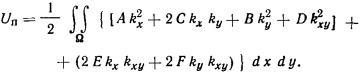
|
(75)
|
При дифференцировании выражения (75) для
потенциальной энергии плиты Uп по
перемещениям Wij после
перехода к конечным разностям ненулевую производную дают слагаемые
потенциальной энергии деформации плиты для узла ij и восьми ближайших к нему узлов (рис.
18).
Выражение частной производной
потенциальной энергии деформации плиты по перемещениям можно представить с
помощью элементарных операторов, приведенных в табл. 66 для различных типов
узлов (рис. 24) (в табл. 66 обозначено 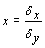 ).Эти операторы получены с использованием выражения (75) и
граничных условий, которые записывают в виде равенства нулю на свободном краю
крутящего и соответствующего изгибающего моментов, что позволяет через
известную по перемещениям на контуре кривизну выразить крутильную и вторую
изгибную кривизны. Заданием в контурных узлах коэффициента жесткости основания,
значительно превышающего величину его для грунтового основания, можно
моделировать жесткие шарнирные опоры. Защемление края плиты имитируется постановкой
таких опор в дополнительном ряду узлов. ).Эти операторы получены с использованием выражения (75) и
граничных условий, которые записывают в виде равенства нулю на свободном краю
крутящего и соответствующего изгибающего моментов, что позволяет через
известную по перемещениям на контуре кривизну выразить крутильную и вторую
изгибную кривизны. Заданием в контурных узлах коэффициента жесткости основания,
значительно превышающего величину его для грунтового основания, можно
моделировать жесткие шарнирные опоры. Защемление края плиты имитируется постановкой
таких опор в дополнительном ряду узлов.
В первых девяти операторах табл. 66 не
учитывается потенциальная энергия деформации изотропного кручения в связи с
тем, что кривизна кручения 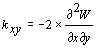 для узлов разностной
сетки записывается с точностью на порядок ниже, чем изгибные кривизны kx и ky. Для
слагаемых, связанных с анизотропией, для одной и той же точки (узла разностной
сетки) необходимо записать вторые однородную и смешанную производные. Кривизны
изотропного кручения в целях повышения точности следует записывать для центров
ячеек. Коэффициент жесткости для узлов разностной
сетки записывается с точностью на порядок ниже, чем изгибные кривизны kx и ky. Для
слагаемых, связанных с анизотропией, для одной и той же точки (узла разностной
сетки) необходимо записать вторые однородную и смешанную производные. Кривизны
изотропного кручения в целях повышения точности следует записывать для центров
ячеек. Коэффициент жесткости 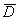 в операторах 10-13 определяют как среднюю для углов
рассматриваемой ячейки величину. в операторах 10-13 определяют как среднюю для углов
рассматриваемой ячейки величину.

Рис.
24. Типы узлов разностной сетки
Элементарные операторы для формирования разрешающих
уравнений при расчете плиты с учетом особенностей деформирования железобетона
Таблица
66
|
Тип
оператора
|
Оператор
|
|
1. Для
внутреннего центрального узла
|
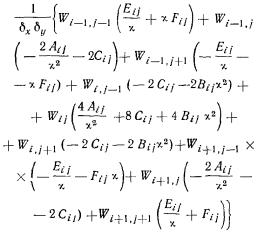
|
|
2. Для
внутреннего верхнего узла
|
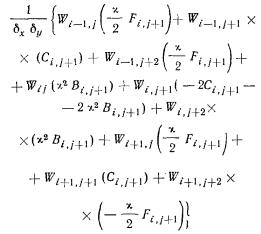
|
|
3. Для
внутреннего правого узла
|
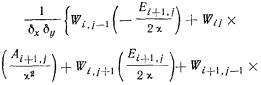

|
|
4. Для внутреннего
нижнего узла
|

|
|
5. Для
внутреннего левого узла
|

|
|
6. Для
внутреннего правого верхнего узла
|
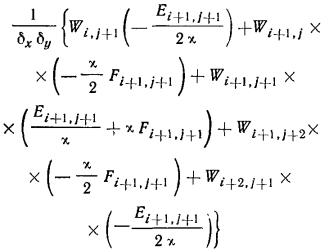
|
|
7. Для
внутреннего правого нижнего узла
|

|
|
8. Для
внутреннего левого нижнего узла
|

|
|
9. Для
внутреннего левого верхнего узла
|


|
|
10. Крутильный
для верхней правой ячейки
|
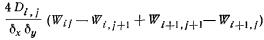
|
|
11. Крутильный
для нижней правой ячейки
|

|
|
12. Крутильный
для нижней левой ячейки
|
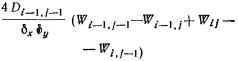
|
|
13. Крутильный
для верхней левой ячейки
|

|
|
14. Для
центрального узла на горизонтальном краю
|

|
|
15. Для
правого узла на горизонтальном краю
|

|
|
16. Для левого
узла на горизонтальном краю
|
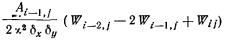
|
|
17. Для
центрального узла на вертикальном краю
|

|
|
18. Для
верхнего узла на вертикальном краю
|

|
|
19. Для
нижнего узла на горизонтальном краю
|

|
В шести последних операторах,
приведенных в табл. 66, обозначено:
|
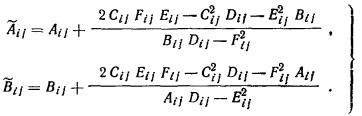
|
(76)
|
При формировании уравнений (65) добавляют выражение (70) к элементу, стоящему на главной диагонали. Правая часть
соотношения (68) представляет собой свободные
члены уравнений (65).
Матрица системы уравнений получается
ленточная симметричная. Ширина ленты равна 4N + 3, где N - число узлов вдоль короткой стороны плиты. В каждой строке
может быть 21 коэффициент, отличный от нуля.
5.24. Вычисление
коэффициентов жесткости плиты как функций кривизны выполняется изложенным ниже
способом.. Записывают кривизны через моменты, пренебрегая мембранными усилиями:
|

|
(77)
|
Коэффициенты жесткости А, В,
С, D, E, F выражают через податливости Bik.
Для этого из уравнения (77) находят моменты, записывают соответствующие
тождества, используя соотношения (73) и (74), и получают:
В выражениях (78) коэффициент В12 = 0, так как с появлением трещин коэффициент поперечной
деформации бетона μ становится
равным нулю.
Различают следующие четыре стадии работы
железобетона:
первая стадия соответствует упругой
работе бетона;
вторая - упругопластической работе бетона
до образования трещин в растянутой зоне;
третья - работе бетона с трещинами или
упругой работе арматуры;
четвертая - работе арматуры в трещинах за
пределом упругости.
В первой и второй стадиях железобетон
рассматривается как изотропный материал и влияние арматуры не учитывается. При
этом больший по абсолютной величине главный момент и момент трещинообразования
связаны неравенством:

Момент трещинообразования определяется по
формуле
|

|
(79)
|
Максимальный по абсолютной величине
главный момент находится по зависимости
|

|
(80)
|
На первой стадии работы железобетона |М|mах ≤
0,5 Мт и коэффициенты
жесткости в соотношениях (73) и (74) соответственно равны:
|

|
(81)
|
Здесь
 - цилиндрическая
жесткость плиты. - цилиндрическая
жесткость плиты.
На второй стадии 0,5Mт ≤ |M|max ≤ Mт и коэффициенты жесткости вычисляют по формулам (81)
после замены D0 на D1:
|

|
(82)
|
Величину D1 можно
записать непосредственно через кривизны, подставив |M|mах в виде
|
|M|max = D1(kmax + μ kmin).
|
(83)
|
При этом kmax - большая, a kmin - меньшая по абсолютной величине главные кривизны,
определяемые по формуле
|
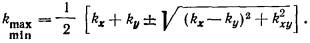
|
(84)
|
В результате получают
|

|
(85)
|
При |M|max > Мт (третья и четвертая стадии работы железобетона) в растянутой
зоне бетона появляются трещины.
Различают три основные схемы трещин в
плите (рис. 25):
непересекающиеся трещины в нижней (схема
1Н) или верхней (схема 1В) зоне;
пересекающиеся трещины в нижней (схема
2Н) или верхней (схема 2В) зоне;
непересекающиеся трещины в нижней и
верхней зонах (схема 3).
Угол между ними и верхними трещинами
считается равным π/2.

Рис. 25. Основные схемы трещин в плите
а -
схема 1Н, а' - схема 1В, б - схема 2Н, б' - схема 2В, в - схема 3
Если трещины в точках плиты не были
зафиксированы ранее, то установив, что Mmax
> Mт, необходимо проверить условия
|
Mmin
> Mт
|
(86)
|
|
Mmin
< -Mт
|
(87)
|
Выполнение условия (86) говорит об
образовании трещин по схеме 2Н. Справедливость соотношения (87) указывает на
образование трещин по схеме 3. Если не выполняются условия (86) и (87), то в
точке плиты образовались непересекающиеся трещины в нижней зоне. Угол наклона
трещин к оси X определяют по формуле
Когда трещины в плите обнаружены, вместо
условий (86) и (87) проверяются неравенства:
|
Mt < Мт
|
(89)
|
|
Mt < -Мт,
|
(90)
|
где
Mt - момент вдоль трещины, равный:
|
Mt = Мх cos2а + Му sin2а - 2 Мху sinа cosа.
|
(91)
|
Выражения для коэффициентов Bik при схеме трещин 1Н имеют вид:
|
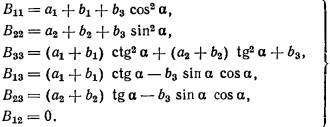
|
(92)
|
В формулах (92) введены обозначения
параметров, из которых формируются жесткостные коэффициенты при любой схеме
трещин:
Для получения Bik в случае схемы трещин 1B в выражениях (92) следует заменить а1 b1 а2, b2 и а
соответственно на а'1, b'1 a'2, b'2, a', т.е.
взять те же параметры (93), но подставлять в них данные не для нижнего, а для
верхнего армирования.
В формулы (93) входит целый ряд
переменных величин, определяемых по-разному в зависимости от стадии работы
арматуры. Границами являются напряжения σуп,
σт (или σ0;2) и σв.
Высота сжатой зоны бетона над трещиной хт и плечи z пар
внутренних сил равны:
|

|
(94)
|
Относительная высота сжатой
зоны ξ определяется по формуле
где
Мп -
изгибающий момент в перпендикулярной трещине плоскости, равный:
|
Мп = Мх sin2а + Му cos2а + Мху sin2а.
|
(96)
|
Предельная величина этого момента
определяется как для балки с коэффициентом армирования μп
|

|
(97)
|
Обобщенный коэффициент армирования
перпендикулярно трещине равен:
|
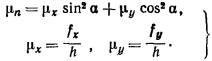
|
(98)
|
Относительная высота сжатой зоны при
текучести арматуры равна;
|

|
(99)
|
где
ξгр вычисляется по
формуле (30) СНиП И-21-75.
Проекция усилий текучести в арматуре на
нормаль к трещине составляет
|

|
(100)
|
Входящие в (95)
величины ξ1 и ξ2 равны:
|

|
(101)
|
где
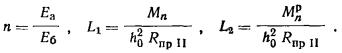
Показатель степени «с» в выражении (95) равен 3, если

Высота сжатой зоны бетона под верхними
трещинами х'т
определяется по тем же формулам (95) - (101) с
заменой величин μп, Nтп, и Мп на
величины μ'п, N'тп, и М'п соответствующие
верхнему армированию.
Бетон сжатой зоны над (или под) трещинами
деформируется как ортотропный материал, оси ортотропии которого параллельны и
перпендикулярны направлению трещин.
Средний модуль деформации сжатого бетона Е'б в перпендикулярном
трещине направлении определяется выражением
|
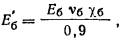
|
(102)
|
в котором:
|

|
(103)
|
Средний модуль деформации Е''б бетона под верхними
трещинами получается из выражений (102) - (103) подстановкой величин М'п, х'т, ξ'i, z = h'0 - 0,5x'т
Деформативность полос бетона вдоль трещин
характеризуется модулем Еп,
который приближенно можно вычислять по формуле
|
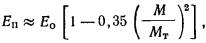
|
(104)
|
где
М -
главный момент, минимальный по модулю из величин Мmax и Mmin.
Средний модуль деформации
арматуры, параллельной оси х, на
любой стадии работы определяется формулой
где
|
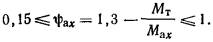
|
(106)
|
Коэффициент vax определяется в зависимости от величины напряжений σах по следующим
формулам:
|
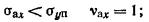
|
(107)
|
при
|

|
(108)
|
где
|
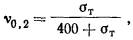
|
(109)
|
при
|

|
(110)
|
|

|
(111)
|
В формулах (109) и (111) напряжения
берутся в МПа.
В формуле (105) величина ψξ
х определяется зависимостью
|

|
(112)
|
В формулу (112) входит расстояние между
трещинами, принимаемое равным большей из двух величин
где
dx,
dу - диаметр арматурных стержней вдоль осей х и у;
μ - коэффициент, принимаемый для арматурных стержней
периодического профиля 0,7, для гладких горячекатаных стержней 1, для арматурной
проволоки 1,25.
Средний модуль деформации арматуры,
параллельной оси Y, E'аy определяется по формулам (105) - (112) с заменой
индекса х на у. При этом в выражении (112) надо
вместо sina
взять cosa.
Коэффициенты λx и λy учитывают влияние касательных напряжений
в арматуре:
где
m1 и m2 -
поправочные коэффициенты при упругопластической стадии работы арматуры (при
упругой стадии работы арматуры коэффициенты m1 и m2 принимают равными 1).
В общем случае коэффициенты m1 и m2
определяют по соотношениям
|

|
(115)
|
где
vax и vay - коэффициенты, определяемые по формулам (107)-(111)
с заменой индекса х на у при нахождении коэффициента vay.
Для вычисления коэффициентов vax,
vay, ψξх
и ψξy необходимо знать величины напряжений в арматуре σaх и σay (или σ'ax и σ'ay), которые нужно найти через моменты последовательными
приближениями
где
|

|
(117)
|
Итеративный процесс нахождения σax и σay начинают с m1 = m2 = 1.
Жесткостные коэффициенты для третьей
схемы трещин (пересекающиеся трещины в разных зонах плиты) получают
суммированием соответствующих величин, вычисленных для схем 1Н и 1В:
|
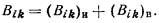
|
(118)
|
При этом b3 в соотношениях (93)
принимают равным нулю. Если трещины возникают по схеме 2Н или 2В
(пересекающиеся трещины в нижней или верхней зонах), податливости равны:
|
В11 = а1
+ b1, В22 = а2 + b2, В12 = В13 = В23 = 0.
|
(119)
|
При вычислении слагаемых в В11 и B22
принимаются:
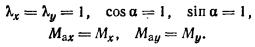
Жесткость на кручение при этой схеме
трещин приближенно принимают равной:

Это допущение не только вносит погрешность,
но и связано с некоторыми неудобствами: видоизменяется матрица системы
уравнений, определяющих прогибы (перемещения) плиты; исключается возможность
использования соотношений (78) для перехода от
податливостей к жесткостным коэффициентам А, В, С, Е, F и D. Поэтому величина В33 для второй схемы трещин
определяется как 1000:D0.
Для любой схемы трещин вычисление
податливостей Вik, выполняется по соотношениям, записанным для схемы
трещин 1Н. Это достигается введением кроме действительного угла α, определяющего направление трещины,
и заданного армирования (fх, fу, f'х, f'у, dx,, dy,
d'x,
d'y,
h0, h'0)
вспомогательных углов β, γ
и δ и расчетного
армирования (fax, fay, daх, day,
h0а). В зависимости от схемы трещин каждой из этих
величин присваивается значение согласно табл. 67. Для схемы трещин 3 вычисление
осуществляется сначала как для схемы 1Н (NT = 5), затем как для схемы 1В при α = α + π/2 (NT = 6) с последующим суммированием.
Таблица
67
|
Тип схемы трещин
|
Значения признака
типа схемы трещин NT
|
Вспомогательные
углы
|
Расчетное
армирование
|
|
β
|
γ
|
δ
|
h0a
|
fax
|
fay
|
dax
|
day
|
|
1Н
|
1
|
α
|
α
|
α
|
h0
|
fx
|
fy
|
dx
|
dy
|
|
IB
|
2
|
α
|
α
|
σ
|
h'0
|
f''x
|
f''y
|
d'x
|
d'y
|
|
1H
|
3
|
π/4
|
0
|
π/2
|
h0
|
fx
|
fy
|
dx
|
dy
|
|
2B
|
4
|
π/4
|
0
|
π/2
|
h'0
|
f''x
|
f''y
|
d'x
|
d'y
|
|
3
|
5
|
α
|
α
|
α
|
h0
|
fx
|
fy
|
dx
|
dy
|
|
6
|
α+π/2
|
α+π/2
|
α+π/2
|
h'0
|
f''x
|
f''y
|
d'x
|
d'y
|
Угол наклона трещины к оси X во всех случаях определяется по формуле (88). Если образовалась верхняя трещина (схема 1В,
NT = 2),
вносится поправка на π/2(α = α + π/2), так как положение
трещины в этом случае определяется не Mmax, a Mmin.
Найденная величина α,
соответствующая моменту появления трещины, в дальнейшем сохраняется независимо
от положения главных площадок тензора моментов. Значение α по абсолютной величине ограничивается
в пределах от 0,01 до 1,56 радиана.
Признак схемы трещин может изменяться
лишь в сторону добавления трещин в узле: к непересекающимся трещинам на нижней
или верхней поверхности плиты могут добавиться пересекающие их трещины в той же
или противоположной зоне.
Суть итеративного процесса, посредством
которого определяются жесткостные коэффициенты при наличии трещин в узле,
показана на рис. 26.

Рис.
26. Принципы итеративного процесса определения жесткостных коэффициентов при
наличии трещин в узле разностной сетки
Мji - моменты (j = x, у, ху; i = 0, 1, 2, ...); Кji - кривизны.
Пусть известны моменты Мjo, соответствующие кривизнам kj, i-1 (j = x,y, xy) в данной точке на предыдущем этапе расчета плиты. Эти
величины фиксируются в качестве координат начального полюса Mjo,
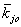 . Пропорционально
приращению кривизн (kji - kj, i-1), где kji - заданные кривизны, принимается приращение расчетных
моментов Мj1. Максимальное приращение моментов ограничивается
величиной, составляющей до 10 % от соответствующего Мj0. По этим
моментам вычисляются податливости Вjk и
кривизны Rj1 (точка 1 на
рис. 26). Новые значения расчетных моментов Mj2 определяются
соотношением . Пропорционально
приращению кривизн (kji - kj, i-1), где kji - заданные кривизны, принимается приращение расчетных
моментов Мj1. Максимальное приращение моментов ограничивается
величиной, составляющей до 10 % от соответствующего Мj0. По этим
моментам вычисляются податливости Вjk и
кривизны Rj1 (точка 1 на
рис. 26). Новые значения расчетных моментов Mj2 определяются
соотношением
|

|
(120)
|
Предварительно расчетные кривизны Rj1 сравниваются
с заданными кривизнами. Если разница между ними лежит в пределах требуемой
точности, то соответствующий момент Мj2 принимается
равным Mj1.
Рассматривая точку 1 как полюс, по
моментам Mj2 вычисляют новые расчетные кривизны  . По
соотношению, аналогичному (120), находятся новые расчетные моменты Мj3. Для этого в
формуле (120) вторые индексы всех ее членов, кроме kji следует увеличить на единицу. Вычисляются новые
расчетные кривизны kj3. С
использованием теперь в качестве полюса точки 2 по той же формуле (120) с заменой индексов находятся новые
расчетные моменты Мj4 и
вычисляются расчетные кривизны kj4 и т. д.
Процесс «микроитерации» продолжается до достижения требуемой точности по
кривизнам. . По
соотношению, аналогичному (120), находятся новые расчетные моменты Мj3. Для этого в
формуле (120) вторые индексы всех ее членов, кроме kji следует увеличить на единицу. Вычисляются новые
расчетные кривизны kj3. С
использованием теперь в качестве полюса точки 2 по той же формуле (120) с заменой индексов находятся новые
расчетные моменты Мj4 и
вычисляются расчетные кривизны kj4 и т. д.
Процесс «микроитерации» продолжается до достижения требуемой точности по
кривизнам.
5.25. Алгоритм расчета плиты составляется по указаниям пп.
5.17 - 5.24.
После ввода и обработки исходных данных выполняется линейный расчет; по
полученным результатам формируется начальный параметр нагрузки t0. соответствующий по линейному решению моменту
трещинообразования в наиболее нагруженной точке плиты; умножением на этот
параметр производится пропорциональный пересчет прогибов, формируется признак
линейного этапа расчета и начинается итеративный процесс решения нелинейной
задачи.
Одна итерация состоит из следующих
операций:
1) вычисление в каждом узле
конечно-разностной сетки коэффициентов жесткости плиты по кривизнам, полученным
в предыдущей итерации. В первой на каждом шаге нагружения итерации расчетные
кривизны принимаются увеличенными в  раз. (Здесь ti
- параметр нагрузки на рассматриваемом i-том шаге нагружения, ti-1 - на
предыдущем шаге). В узлах, лежащих на контуре, кривизны вычисляются с учетом
граничных условий; раз. (Здесь ti
- параметр нагрузки на рассматриваемом i-том шаге нагружения, ti-1 - на
предыдущем шаге). В узлах, лежащих на контуре, кривизны вычисляются с учетом
граничных условий;
2) формирование и решение
системы разрешающих уравнений. Для сокращения числа обращений к внешним
запоминающим устройствам при большом числе узлов разностной сетки уравнения
формируются блоками, каждый из которых соответствует одному ряду узлов по
короткой стороне плиты. По мере формирования и обработки по схеме «прямого
хода» блоки уравнений записываются на диски (при использовании ЭВМ серии ЕС).
После формирования всех уравнений выполняется «обратный ход».
Автоматизированное формирование матрицы разрешающих уравнений позволяет
уменьшить число типов узлов для прямоугольной плиты с 25 до 9;
3) после анализа признака
этапа расчета, показавшего что выполняется очередная итерация нелинейного
расчета, необходимо перейти к оценке достигнутой точности решения по прогибам.
Приращение перемещений в любом узле должно быть меньше заданной доли
максимального прогиба, соответствующего начальному параметру нагрузки t0, умноженной на шаг приращения параметра нагрузки ∆t. Если точность недостаточная, то выполняется следующая
итерация. При достижении требуемой точности увеличивается параметр нагрузки
Расчет завершается при достижении
заданной нагрузки.
5.26. Учет нелинейности деформирования железобетона
позволяет увеличить, как правило, допустимую нагрузку за плиту за счет
перераспределения и уменьшения максимальных значений усилий, но при этом
обнаруживается резкое возрастание неравномерности осадок. Данные нелинейного
расчета позволяют выполнить достоверную оценку работы конструкции по предельным
состояниям второй группы. Для определения ширины раскрытия трещин используют
формулу
|
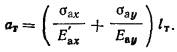
|
(122)
|
Параметры, входящие в формулу (122),
вычисляют по формулам (105), (113), (116).
5.27. Изложенный выше алгоритм реализован в программе НРП-1
для ЭВМ серии ЕС. Программа составлена на алгоритмическом языке FORTRAN.
Позволяет рассчитывать плитные фундаменты
с произвольно заданной переменной толщиной и переменным армированием. При
использовании в качестве внешних запоминающих устройств магнитных дисков число
узлов разностной сетки при расчете плиты может достигать 2000.
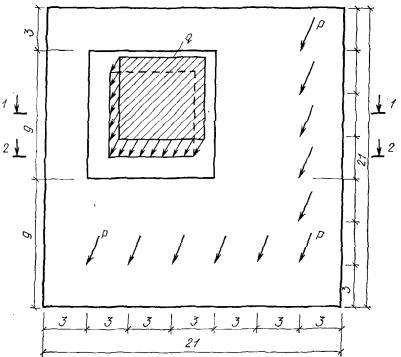
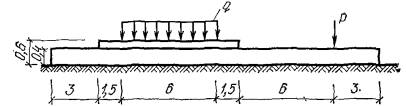
Рис.
27. Схема плитного фундамента
Пример.
Размеры плиты и ее загружение показаны на
рис. 27.
При расчете приняты:
бетон марки М350;
арматура класса А-III горячекатаная;
процент армирования для верхней арматуры
в обоих направлениях 0,2; для нижней 0,5;
диаметр нижней арматуры 20 мм, верхней 10
мм;
защитный слой бетона для нижней и верхней
арматуры 3 см;
коэффициент жесткости основания 8 МН/м3.
На рис. 28 и 29 приведены эпюры прогибов,
изгибающих и крутящих моментов в сечениях 1-1, 2-2, соответствующие нагрузкам q = 0,16 МН/м2 и Р = 1,1 МН. Максимальное раскрытие трещин при этом равно 0,41 мм.
Нагрузка трещинообразования, определенная из линейного решения, составляет от
расчетной 29,3 %.
Анализ результатов показывает, что учет
нелинейности деформирования железобетона выявляет существенное
перераспределение усилий в сторону уменьшения пиков и увеличения
неравномерности осадок.
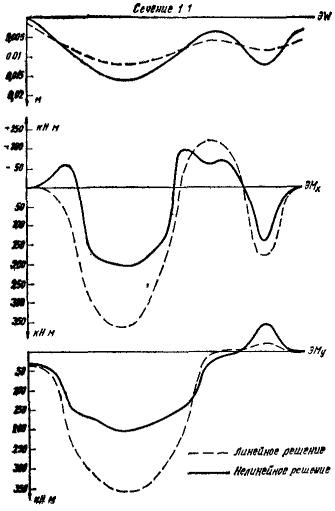
Рис. 28. Перемещения и моменты в сечении 1-1
( линейное
решение, линейное
решение,  нелинейное решение) нелинейное решение)

Рис. 29. Перемещения и моменты в сечении 2-2
( линейное решение, линейное решение,
 нелинейное решение) нелинейное решение)
5.28. Совместный
расчет плитного фундамента произвольной формы в плане постоянной либо
переменной толщины на сжимаемом основании и стержневого рамного каркаса здания
наиболее рационально выполнять путем приведения каркаса здания и плитного
фундамента к единой стержневой конструкции, для чего плитный фундамент следует
заменить эквивалентной по жесткости системой перекрестных балок по расчетной
схеме 2 (по п.
5.7).
5.29. Выбор жесткостей балок должен выполняться по
следующему правилу: на фундамент наносится прямоугольная сетка (рис. 30, а) с постоянными шагами
α и β вдоль осей ОХ
и ОУ, являющаяся
осями стержней системы перекрестных балок. Изгибная н крутильная жесткости балок подсчитываются с помощью соотношений:
|

|
(123)
|
где
D -
цилиндрическая жесткость плитного фундамента.
Жесткости балок, идущих по контуру,
уменьшаются вдвое.
5.30. Ширина подошвы всех стержней принимается одинаковой;
она определяется из условия равенства опорных площадей исходного фундамента и
заменяющей его системы перекрестных балок. В частности, для прямоугольного
фундамента с размерами lx и ly в плане, с n ячейками сетки в продольном и m в
поперечном направлениях ширина подошвы равна:
|
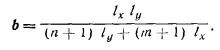
|
(124)
|

Рис.
30. Схема для расчета плитного фундамента
а - узлы, стержни прямоугольной сетки
О - номера узлов, -
номера стержней
б - узел "0" разностной сетки
α,
β - шаг стержней системы перекрестных балок в - взаимное расположение
узлов разностной сетки: х -
законтурный узел, 1 - контурный
узел, 2 - первый и второй внутриконтурные узлы; wx - перемещение законтурного узла, w1 - перемещение контурного узла, w2 и w5 - перемещения внутриконтурных узлов
Для квадратного фундамента при lx
= ly=
l и m = n
|

|
(125)
|
5.31. Допускается, чтобы сетка осей системы перекрестных
балок была косоугольной. При этом одно из направлений сетки должно быть
параллельно оси ОХ или
оси ОУ. Другое
направление не должно меняться, отрезки контура фундамента должны быть
параллельны направлениям сетки.
5.32. После замены фундамента эквивалентной по жесткости
системой перекрестных балок все сооружение в целом представляет собой
пространственную (в частном случае плоскую) стержневую конструкцию, для
статического расчета которой принимается метод перемещений строительной
механики. При этом в каждый узел каркаса вводится по 6 (по 3) связей,
соответствующих всем степеням свободы точек пространственного (плоского)
сооружения. Для узлов фундаментной части, находящихся в контакте с грунтовым
основанием, число связей (степеней свободы) уменьшается; для пространственного
сооружения оно равно 3 (связи соответствуют вертикальному перемещению Δz и 2 поворотам вокруг взаимно перпендикулярных
горизонтальных осей φx и φу), для плоского - 2 (Δz и φу).
5.33. В соответствии с общим алгоритмом метода перемещений
составляется система линейных алгебраических уравнений, элементы матрицы
которой являются реакциями в связях от их единичных перемещений, а элементы
столбцов свободных членов - реакциями в связях от внешних воздействий. При этом
каждый из столбцов свободных членов соответствует одному варианту загружения.
5.34. Реакции в связях от их единичных перемещений и от
внешних воздействий для стержней каркаса и для балок фундаментной части при
расчетной схеме основания, характеризуемой переменным или постоянным
коэффициентом жесткости, определяются по известным формулам строительной
механики с учетом или без учета интеграла поперечных сил. Интегралы моментов
для всех стержней и интеграл нормальных сил для стержней каркаса учитываются
всегда.
5.35. Для определения реакций в связях узлов фундаментной
части конструкций от стержней системы перекрестных балок в случае, когда для
основания используются расчетные схемы, обладающие распределительным свойством,
например линейно-деформируемое полупространство, слой и др., необходимо
применить следующую процедуру:
а) каждый стержень системы
перекрестных балок контактирует с основанием по прямоугольной площадке длиной
α или β и шириной b. В центре площадки вводим
стержень-связь между основанием и стержнем системы балок и всем этим связям
присваиваем подряд идущие номера от 1 до n, где n - количество стержней системы
перекрестных балок;
б) в соответствии с методом
Б.Н. Жемочкина для каждой такой стержневой связи можно записать следующее
уравнение:
|
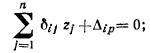
|
(126)
|
в) составив подобные уравнения
для всех связей i (i = 1, 2, , n), получим систему линейных
алгебраических уравнений порядка n, называемую
вспомогательной. Ee матрица является суммой двух
матриц
|

|
(127)
|
где
{δ(0)ij} -
полностью заполненная матрица осадок основания;
{δ(1)ij} -
диагональная матрица перемещений балок перекрестной системы.
В выражении (127) осадка
граничной поверхности основания в точке приложения связи i от
единичной силы, равномерно распределенной по прямоугольной площадке, центр
которой совпадает с точкой приложения связи j, обозначена δ(0)ij. Способ вычисления этой величины
δ(0)ij зависит от выбранной расчетной схемы основания.
Перемещение середины стержня δ(1)ij &JP над i-той связью от единичной силы, приложенной в этой же
точке, т.е. при i = j, вычисляется по следующей формуле (при i ≠ j δ(1)ij = 0);
|

|
(128)
|
где
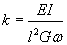 , EI и Gω -
изгибная и приведенная сдвиговая жесткости балки над i-той
связью; , EI и Gω -
изгибная и приведенная сдвиговая жесткости балки над i-той
связью;
l -
длина балки.
Для неучета поперечных сил достаточно
положить k = 0;
г) способ вычисления столбцов
свободных членов зависит от вида воздействия на конструкцию. Количество
столбцов свободных членов равно: 3N(2N) + k, где N - число узлов фундаментов части
(системы перекрестных балок), k - количество
вариантов загружений, действующих на сооружение. Каждому из узлов дается по 3
(для плоской конструкции по 2) единичных перемещения, соответствующих
наложенным на него связям, и в стержнях, примыкающих к этому узлу, вычисляются
возникающие при этом перемещения. От внешней нагрузки, приложенной к стержням,
вычисляются перемещения стержней; от внешних нагрузок, приложенных к основанию
(например, от пригрузок на его поверхности, от просадок в районах горных
выработок), вычисляются перемещения основания. Все эти перемещения и являются
элементами столбцов свободных членов;
д) сформированная система
линейных уравнений решается, и ее решение представляет собой отпоры (реакции в
связях по центрам опорных площадок балок), возникающие под стержнями
фундаментной части в основной системе метода перемещений от единичных
перемещений связей этого метода и от внешней нагрузки;
е) от этих отпоров вычисляются
реакции в связях метода перемещений, которые и являются элементами матрицы
реакций н столбцов свободных членов этого метода соответственно. К элементам
матрицы реакций, вычисленным таким образом, необходимо добавить реакции от
деформации стержней фундаментной части, найденные как для обычных стержней
каркаса.
5.36. В общем случае при формировании матрицы реакций и
столбцов свободных членов метода перемещений необходимо учитывать наличие
бесконечно-жестких участков по концам стержней, произвольные граничные условия
в местах примыкания гибкой части стержня к бесконечно жесткому участку и
произвольную ориентацию стержней в пространстве и на плоскости основания.
Окончательная матрица реакций стержня с учетом всех этих факторов вычисляется с
помощью матричного соотношения
|

|
(129)
|
Окончательный вектор реакций столбца
свободных членов этого же стержня находится с помощью соотношения
|

|
(130)
|
В выражениях (129) и (130) R и Rp
- матрица реакций и вектор свободных
членов от внешней нагрузки в стержне и его местной системе координат при обоих
защемленных концах; В -
матрица переноса, содержащая размеры жестких участков в узлах; С - матрица направляющих косинусов
перехода к общей системе координат; штрих обозначает операцию транспонирования
матрицы; звездочка - операцию учета реальных граничных условий с помощью
жордановых исключений.
5.37. Решение системы линейных алгебраических уравнений
метода перемещений дает перемещения узлов конструкции в порядке их нумерации и
в соответствии с принятым количеством степеней свободы в рассматриваемом узле
для каждого варианта загружения в отдельности. Среди этих перемещений имеются и
вертикальные перемещения узлов системы перекрестных балок, аппроксимирующих
фундаментную плиту.
5.38. Усилия в фундаменте вычисляются по вертикальным
перемещениям узлов сетки с помощью конечно-разностных соотношений. Ниже
приводятся выражения для изгибающих и крутящего момента для некоторой точки О на плите через перемещения этой
точки и окружающих точек (рис. 30, б):
|
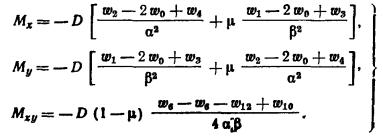
|
(131)
|
Здесь μ - коэффициент Пуассона
материала плиты. Помимо моментов в каждой точке плиты вычисляются обычная и
кирхгофовская поперечные силы и отпор основания.
В точках, лежащих на краях фундамента,
параллельных оси ОХ, вычисляются
только Мх, Qx и отпор основания; в точках,
лежащих на краях, параллельных оси ОУ, вычисляются только Му, Qy и отпор основания; в наружных
угловых точках вычисляется только отпор основания. В точках, являющихся
вершинами входящих углов, усилия вычисляются так же, как и во внутренних
точках.
5.39. При вычислении усилий в контурных точках и в точках
первого внутриконтурного ряда (для перерезывающих сил) необходимо знать
перемещения первого законтурного ряда. Эти перемещения вычисляются с помощью
квадратичной экстраполяции по перемещениям трех соответствующих соседних точек
фундамента (рис. 30, в) по следующим формулам:
|

|
(132)
|
где
wx - искомое перемещение
законтурной точки.
5.40. Отпор основания, описываемого переменным
коэффициентом жесткости, определяется в каждом узле сетки по формуле
|

|
(133)
|
где
ki - коэффициент жесткости в узле i. Если в точке сходится несколько
стержней с различными коэффициентами жесткости, то ki, принимается равным их среднеарифметическому
значению.
5.41. При расчетной схеме основания, обладающего
распределительным свойством (линейно-деформируемое полупространство, слой и
др.), отпор грунта вычисляется с помощью векторного равенства
|
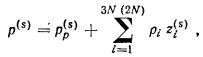
|
(134)
|
где
s -
номер очередного варианта загружения;
3N(2N) - количество связей метода перемещений, наложенных на
узлы фундаментной части конструкции;
z(s)i - перемещение i-той связи в s-м варианте загружения;
p(s)p - грузовой отпор в основной системе, возникающий под
балками перекрестной системы в s-м варианте загружения;
рi - такой же отпор, возникающий от единичного
перемещения i-той связи.
Поскольку под каждым стержнем системы
перекрестных балок имеется только одна площадка контакта с упругим основанием,
то порядок вектора р(s) равен
количеству этих стержней (порядку вспомогательной системы уравнений), и каждый
элемент вектора равен отпору под соответствующим стержнем. Отпор основания в
узле полагается равным среднему арифметическому из отпоров под стержнями,
сходящимися в этом узле.
5.42. В результате выполнения статического расчета
определяются эпюры усилий и перемещений в плитном фундаменте для каждого из
заданных вариантов загружений. Затем по этим эпюрам подсчитываются комбинации
усилий и перемещений во всех точках фундамента. Подсчет ведется в соответствии
с главами СНиП на нагрузки и воздействия и на строительство в сейсмических
районах для обеих групп предельных состояний. Для первой группы определяются
расчетные комбинации усилий для 1-го и 2-го основных и особых с сейсмикой или
без сейсмики сочетаний. Для второй группы определяются нормативные комбинации
усилий и перемещений для 1-го и 2-го основных и особого без сейсмики сочетаний.
При расчете учитывается возможная несовместность некоторых вариантов
загружений. Предусмотрены следующие виды нагрузок: постоянные, снеговые,
временные длительные, кратковременные, климатические, ветровые, крановые от
кранов легкого, среднего, тяжелого и весьма тяжелого режимов работы,
сейсмические и особые несейсмические (например, деформации поверхности
основания в районах горных выработок или его просадки в районах просадочных или
карстовых грунтов). Учитывается также требование СНиП о том, что для некоторых
видов нагрузок при выборе комбинаций по 2-й группе предельных состояний часть
воздействия является длительной, а часть - кратковременной.
На следующем этапе расчета по найденным
комбинациям расчетных усилий определяется продольное и поперечное армирование
во всех точках плитного фундамента. Площадь арматуры вычисляется в соответствии
с главой СНиП по проектированию бетонных и железобетонных конструкций. В каждой
точке фундамента, для которой известны комбинации усилий, определяются верхняя
и нижняя продольная арматура обоих направлений, поперечная арматура обоих
направлений и ее шаг в каждом из них и отогнутая арматура обоих направлений.
Марка бетона может быть любой из предусмотренных упомянутой главой СНиП,
арматура может быть классов A-I, A-II, и А-III. Таким
образом, в результате расчета плитного фундамента по программе ПРОФКОН
формируются все необходимые данные, которые инженер-проектировщик может
непосредственно использовать при конструировании этого фундамента.
5.43. Замена плиты перекрестной системой балок использована
для расчета каркаса совместно с плитой также в программе ЦНИИСК-100. Эта
программа предназначена, кроме того, для расчета в условиях, когда в процессе
эксплуатации каркасных зданий по каким-либо причинам возникают просадки
основания.
Программа ЦНИИСК-101, предназначенная для
расчета плитных фундаментов переменной толщины с учетом физической нелинейности
железобетона и грунта, также учитывает возможность проявления в процессе
эксплуатации сооружений просадок.
Пример расчета плитного фундамента по программе
ПРОФКОН
Задан плитный фундамент размером в плане
30 × 37,5 м. На фундамент наносим сетку, состоящую из 4 × 4 ячеек,
как показано на рис. 30. На этом же рисунке показана нумерация узлов и
стержней. Для упрощения расчета принята модель основания с постоянным
коэффициентом жесткости К-3 МН/м3. Коэффициент Пуассона материала
конструкции равен 0,2.
Цилиндрическая жесткость 73500 кПа·м4.
Отсюда получаем изгибные жесткости стержней системы перекрестных балок:

Таблица 68
|
Узел (точка)
|
Значения сил в загружении, кН
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
1
|
96,9
|
52,7
|
52,7
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
2
|
96,9
|
52,7
|
52,7
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
3
|
77,2
|
46,8
|
-1,8
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
4
|
77,2
|
46,8
|
95,3
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
5
|
81,7
|
49,2
|
49,2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
6
|
193,7
|
39,5
|
105.3
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
7
|
193,7
|
39,5
|
105,3
|
200
|
-
|
-
|
-
|
-
|
-
|
-
|
|
8
|
154,3
|
27,7
|
-3,5
|
-
|
-
|
-
|
-
|
-
|
-200
|
200
|
|
9
|
154,3
|
27,7
|
190,5
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
10
|
163,3
|
32,5
|
32,5
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
11
|
193,7
|
171,1
|
105,3
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
12
|
193,7
|
171,1
|
105,3
|
-
|
-
|
-
|
200
|
-200
|
-
|
-
|
|
13
|
154,3
|
159,3
|
-3,5
|
-
|
-
|
200
|
-
|
-
|
-
|
-
|
|
14
|
154,3
|
159,3
|
190,5
|
-
|
-
|
-
|
-200
|
200
|
-
|
-
|
|
15
|
163,3
|
164,1
|
98,3
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
16
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
17
|
117,2
|
63,2
|
63,2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
18
|
77,2
|
46,8
|
-1,8
|
-
|
-
|
-
|
-
|
-
|
200
|
-200
|
|
19
|
77,2
|
46,8
|
95,3
|
-
|
200
|
-
|
-
|
-
|
-
|
-
|
|
20
|
100,7
|
67,4
|
67,4
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
21
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
22
|
29,7
|
16,2
|
16,2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
23
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
24
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
25
|
29,7
|
16,2
|
16,2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
Таблица 69
|
Усилия и
перемещения
|
Номера точек (узлов)
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
Осадка W
|
-18,6
|
-10,9
|
-8,2
|
-8,8
|
-15,2
|
-19,6
|
-13,3
|
-10,6
|
-10,9
|
-16,8
|
-1,62
|
-12,6
|
|
Угол поворота TGY
|
-0,1
|
-0,3
|
-0,4
|
-0,3
|
-0,2
|
0,0
|
-0,2
|
-0,3
|
-0,2
|
-0,2
|
1,1
|
0,5
|
|
Угол поворота TGX
|
-1,4
|
-0,6
|
-0,2
|
0,4
|
1,3
|
-1,2
|
-0,5
|
-0,2
|
0,3
|
1,2
|
-0,8
|
-0,3
|
|
Изгибающий момент MX
|
|
-5,3
|
-3,3
|
-6,6
|
|
|
-3,5
|
-2,8
|
-6,3
|
|
|
-0,1
|
|
Изгибающий момент МУ
|
|
|
|
|
|
7,9
|
5,3
|
4,6
|
3,6
|
3,3
|
11,8
|
8,5
|
|
Крутящий момент MXY
|
|
|
|
|
|
|
-1,5
|
-0,0
|
0,5
|
|
|
-2,7
|
|
Поперечная сила OX
|
|
-0,1
|
-0,2
|
-0,3
|
|
|
-0,2
|
-0,2
|
-0,3
|
|
|
-0,3
|
|
Поперечная сила OY
|
|
|
|
|
|
-0,7
|
-0,6
|
-0,3
|
-0,3
|
-0,3
|
0,4
|
-0,3
|
|
Кирхгофова сила QKX
|
|
-0,3
|
-0,2
|
-0,3
|
|
|
-0,4
|
-0,3
|
-0,3
|
|
|
-0,6
|
|
Кирхгофова сила QKY
|
|
|
|
|
|
-1,0
|
-0,9
|
-0,4
|
-0,3
|
-0,4
|
-0,1
|
-0,8
|
|
Отпор основания P
|
5,6
|
3,3
|
2,4
|
2,6
|
4,6
|
5,9
|
4,0
|
3,2
|
3,3
|
5,0
|
4,9
|
3,8
|
|
Нормальная сила N
|
96,9
|
96,9
|
77,2
|
77,2
|
81,7
|
193,7
|
193,7
|
153,3
|
154,3
|
163,3
|
193,7
|
193,7
|
Продолжение таблицы 69
|
Усилия и
перемещения
|
Номера точек (узлов)
|
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
|
Осадка W
|
-10,5
|
-10,6
|
-16,1
|
-6,8
|
-7,6
|
-6,3
|
-6,4
|
-11,4
|
0,7
|
-1,3
|
-0,4
|
-0,6
|
-5,4
|
|
Угол поворота TGY
|
0,4
|
0,4
|
0,5
|
1,5
|
1,0
|
0,9
|
0,9
|
1,0
|
1,1
|
1,0
|
1,0
|
1,0
|
1,0
|
|
Угол поворота TGX
|
-0,2
|
0,3
|
1,2
|
-0,1
|
-0,0
|
-0,2
|
0,3
|
1,0
|
0,2
|
0,1
|
-0,2
|
0,3
|
0,9
|
|
Изгибающий момент MX
|
-1,3
|
-5,5
|
|
|
3,3
|
-1,2
|
-5,9
|
|
|
4,3
|
-0,8
|
-5,4
|
|
|
Изгибающий момент МУ
|
7,6
|
6,5
|
6,6
|
-3,2
|
3,2
|
3,0
|
1,8
|
1,4
|
|
|
|
|
|
|
Крутящий момент MXY
|
-0,4
|
0,3
|
|
|
-2,2
|
-0,4
|
0,2
|
|
|
|
|
|
|
|
Поперечная сила OX
|
-0,4
|
-0,3
|
|
|
0,2
|
-0,6
|
-0,3
|
|
|
0,1
|
-0,6
|
-0,3
|
|
|
Поперечная сила OY
|
0,0
|
0,1
|
0,1
|
0,9
|
0,1
|
0,3
|
0,3
|
0,4
|
|
|
|
|
|
|
Кирхгофова сила QKX
|
-0,5
|
-0,3
|
|
|
0,5
|
-0,6
|
-0,4
|
|
|
0,5
|
-0,6
|
-0,4
|
|
|
Кирхгофова сила QKY
|
-0,1
|
0,0
|
0,0
|
0,5
|
-0,3
|
0,2
|
0,2
|
0,3
|
|
|
|
|
|
|
Отпор основания P
|
3,1
|
3,2
|
4,8
|
2,1
|
2,3
|
1,9
|
1,9
|
3,4
|
-0,2
|
0,4
|
0,1
|
0,2
|
1,6
|
|
Нормальная сила N
|
154,3
|
154,3
|
163,3
|
|
17,2
|
77,2
|
77,2
|
100,7
|
|
29,7
|
|
|
29,7
|
Таблица 70
|
Первая группа предельных состояний
|
|
Вид сочетания
|
Знак усилия
|
Изгибающий момент
MX
|
Изгибающий момент
MY
|
Крутящий момент
MXY
|
Перерезывающая
сила QX
|
Перерезывающая
сила QY
|
Кирхгофова сила
QKX
|
Кирхгофова сила
QKY
|
Отпор основания
P
|
Нормальная
сила
N
|
|
Первое сочетание
|
МАХ
|
13,64
|
27,33
|
-0,56
|
0,36
|
1,90
|
0,27
|
2,50
|
10,75
|
646,83
|
|
MIN
|
-16,89
|
1,02
|
-5,22
|
-5,08
|
-5,08
|
-2,78
|
-6,67
|
2,73
|
174,33
|
|
Второе основное
|
МАХ
|
17,31
|
26,57
|
-0,53
|
0,49
|
3,32
|
0,29
|
4,20
|
11,62
|
620,83
|
|
MIN
|
-16,90
|
0,96
|
-6,17
|
-2,65
|
-4,83
|
-3,31
|
-6,34
|
7,79
|
174,33
|
|
Особое с сейсмиче-
ским
|
МАХ
|
7,49
|
20,44
|
0,19
|
1,78
|
0,74
|
2,38
|
0,68
|
9,01
|
460,77
|
|
MIN
|
-11,41
|
-1,70
|
-4,94
|
-3,31
|
-2,47
|
-4,58
|
-3,07
|
2,78
|
156,90
|
|
Вторая группа предельных состояний
|
|
Вид сочетания
|
Знак усилия
|
Осадка
W
|
Угол поворота
TGY
|
Изгибающий момент
MX
|
Изгибающий момент
MY
|
Осадка
W
|
Угол поворота
TGX
|
Угол поворота
TGY
|
Изгибающий момент
MX
|
Изгибающий момент
MY
|
|
Первое основное
|
ОБА
|
-10,89
|
0,28
|
9,41
|
22,00
|
-30,51
|
-1,32
|
-1,29
|
-14,37
|
2,16
|
|
Второе основное
|
ОБА
|
-11,08
|
0,25
|
12,58
|
21,43
|
-32,92
|
-1,44
|
-1,30
|
-14,34
|
2,12
|
Крутильные жесткости стержней
принимаем равными изгибным:
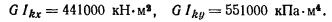
Ширина подошвы стержней

Рассматриваем действие на фундамент 10 вариантов
загружений. В каждом из них приложены сосредоточенные узловые силы. Значения
этих сил в кН приведены в табл. 68.
Первое загружение является постоянным;
2-е и 3-е - временные длительные; с 4-го по 6-е - кратковременные; 7-е и 8-е -
ветровые; 9-е и 10-е - сейсмические. Коэффициенты перегрузки, соответствующие
этим загружениям, равны 1,1; 1,2; 1,3; 1,2; 1,0. Исходные данные для подбора арматуры
по всему фундаменту таковы: марка бетона М200, продольная арматура класса А-II, поперечная класса A-I. Толщина плиты
0,7 м, верхний защитный слой 0,035 м, нижний защитный слой 0,05 м. В тех
местах, где по расчету понадобятся отгибы, их угол наклона равен 45°.
Ввиду большого объема результатов расчета
здесь приводится только часть, а именно: исходная информация (табл. 68); усилия и перемещения в плитном фундаменте от
1-го загружения (табл. 69), комбинации
усилий в точке 7 (табл. 70) и
результаты подбора арматуры по всему фундаменту (табл. 71).
5.44. Комплекс
программ «Плиска» предназначен для автоматизированного расчета плитного
фундамента совместно с каркасом наземной части как единой пространственной
системы на ЭВМ «Минск-32» и «ЕС-1022». В комплексе автоматизированы этапы
формирования расчетной модели на основе информации об архитектурном описании
объекта; решения задачи строительной механики; выбора параметров плиты и
определения сечений арматуры с внутримашинной передачей информации от этапа к
этапу.
5.45. В комплексе
обеспечена возможность описания системы на уровне конструктивных элементов с
чертежа; задания сложной конфигурации плиты; задания переменных свойств
основания и переменной толщины в плане; визуального контроля графической
информации введенной в ЭВМ конструктивной схемы, вычерченной графопостроителем;
вывода на печать автоматически построенной расчетной модели с нумерацией узлов
и элементов; вывода на печать усилий и перемещений в элементах системы;
определения минимально допустимых размеров плиты в плане и толщины под
колоннами из условий продавливания; выбора и унификации размеров банкеток под
колонны по высоте и в плане.
Таблица 71
Результаты подбора арматуры в фундаменте
|
Вид арматуры
|
Номера точек (узлов)
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
|
FAX ВЕРХНЯЯ
|
3,3
|
9,2
|
9,9
|
8,6
|
3,3
|
3,3
|
9,7
|
14,0
|
11,6
|
3,3
|
3,3
|
111,8
|
8,4
|
16,2
|
3,3
|
3,3
|
3,3
|
10,2
|
9,5
|
3,3
|
3,3
|
3,2
|
4,6
|
6,9
|
3,3
|
|
FAX НИЖНЯЯ
|
3,2
|
3,2
|
3,2
|
3,2
|
3,2
|
3,2
|
10,2
|
6,1
|
6,5
|
3,2
|
3,2
|
12,2
|
9,0
|
14,7
|
3,2
|
3,2
|
7,4
|
6,7
|
10,8
|
3,2
|
3,2
|
6,3
|
3,2
|
3,2
|
3,2
|
|
FAY ВЕРХНЯЯ
|
3,3
|
3,3
|
3,3
|
3,3
|
3,3
|
3,2
|
3,3
|
8,5
|
3,3
|
3,4
|
3,2
|
5,5
|
3,2
|
6,6
|
3,3
|
5,5
|
3,3
|
7,6
|
3,3
|
3,3
|
3,3
|
3,3
|
3,3
|
3,3
|
3,3
|
|
FAY НИЖНЯЯ
|
3,2
|
3,2
|
3,2
|
3,2
|
3,2
|
13,3
|
16,4
|
11,5
|
6,8
|
3,7
|
27,3
|
28,3
|
24,9
|
30,1
|
23,0
|
3,2
|
6,2
|
12,7
|
17,0
|
12,6
|
3,2
|
3,2
|
3,2
|
3,2
|
3,2
|
5.46. Пространственную
структуру здания определяют в плане набором продольных и поперечных разбивочных
осей здания, а по высоте - поэтажным делением. В бланки исходной информации
записывают наименования осей, указывают расстояние между ними и высоты этажей.
5.47. Положение
элемента стены в каркасе однозначно определяют наименованиями разбивочных осей,
вдоль которых расположены элементы стен (жесткости), наименованиями осей
другого направления, между которыми расположены элементы стен, и номером этажа,
на котором имеется описываемый элемент. Конструктивный элемент стены
«вставляют» в пространственную решетку и характеризуют толщиной и маркой
бетона.
5.48. Диски перекрытий, объединяющие стены по высоте и
обеспечивающие совместную пространственную работу плиты, стен и перекрытий, не
описывают, а формируют автоматически на заданных этажах по контуру здания и
положению стен и колонн в плане.
5.49. Плитный фундамент задают координатами угловых точек
контура и зон утолщений, характеризуют толщиной и маркой бетона. В плане плита
представляет собой многоугольник с ортогональными сторонами, возможно, с
проемами, с произвольным числом узлов. Толщина плиты ступенчато-переменная.
5.50. Основание представлено в плане переменным
коэффициентом жесткости, определяемым по ожидаемым осадкам.
5.51. Статический расчет ведется
в линейной постановке методом конечных элементов в перемещениях. Расчетной
моделью является композитная система, состоящая из плоских прямоугольных
конечных элементов, соединенных в узлах. Конечные элементы образуют в
результате нанесения на здание пространственной сетки. Формирование расчетной
модели автоматическое. Метод конечных элементов позволяет на основе
универсального подхода рассчитать единую
сложную пространственную систему из двумерных элементов на упругом основании и
определить характер взаимодействия стен, перекрытий, фундаментной плиты.
5.52. Плитный
фундамент моделируют пластинами на упругом основании с изгибной группой усилий,
стены жесткости - пластинами с изгибной и мембранной группами усилий, перекрытия
- пластинами с мембранной группой усилий. Жесткости всех элементов конечны и
вычисляют по толщине и марке бетона автоматически.
5.53. Алгоритм расчета комплекса «Плиска» методом конечного
элемента в перемещениях сводится к следующему:
1. Осуществляется автоматическое
построение расчетной модели системы как совокупности объектов строительной
механики исходя из конструктивного описания. Организуется приведение исходной
информации к виду, используемому в методе конечных элементов, а именно:
наносится расчетная сетка на
конструктивные элементы плиты, стен, перекрытий, т.е. делается разбивка на
конечные элементы - пластины. Сетка генерируется автоматически и проходит через
точки, лежащие на пересечении осей, углы контуров плиты и перекрытий, стены,
колонны, зоны нагрузок и основания, зоны утолщения плиты. Анализируются
расстояния между соседними линиями сетки. В случае если оно более
регламентированного программой, проводится дополнительная разбивка; нумерация
узлов пространственной модели осуществляется автоматически так, чтобы ширина
ленты матрицы системы уравнений была минимальна, т.е. для пространственной
ортогональной сетки проводится сквозная нумерация плоскостей по «меньшей
грани»;
вычисляются координаты узловых точек в
общей системе координат - правой ортогональной, расположенной в левом нижнем
углу плиты;
формируется массив элементов -
топологическая последовательность конечных элементов, увязывающая положение
элемента в структуре с номерами принадлежащих ему узлов;
вычисляются геометрические и жесткостные
характеристики элементов по конструктивному описанию;
осуществляется приведение значений
нагрузок к номерам узлов (по загружениям).
2. Формируются матрицы
жесткости для элементов в местной системе координат.
Жесткостные характеристики
конечных элементов могут быть определены на основании принципа возможных
перемещений
|

|
(135)
|
для плосконапряженных элементов, где
εx, εy, γху, Nx, Ny, Txy - соответственно
деформации и погонные усилия, и
|

|
(136)
|
для изгибаемых конечных элементов типа
плит; обозначения такие же, как в п. 5.11. В матричной форме
|
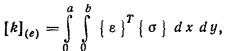
|
(137)
|
где компоненты деформации {e}e и
погонных усилий {σ}e выражают
через неизвестные узловые перемещения:
|

|
(138)
|
|
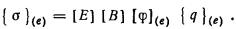
|
(139)
|
Перемещения аппроксимируют
кусочно-полиномиальными функциями
|
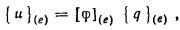
|
(140)
|
где
[В] - матрица дифференциальных операторов;
[Е] - матрица упругих свойств;
{q}(e) - вектор узловых неизвестных элемента;
[φ](е) -матрица,
элементами которой служат функции формы.
Порядок квадратной матрицы жесткости [k](e) равен
числу степеней свободы рассматриваемого элемента.
3. Формируются матрицы
жесткости для всей системы. Для каждого элемента определяется матрица
направляющих косинусов и с помощью матрицы преобразования [е] переводится матрица
жесткости элемента из местной системы координат в общую в виде
|

|
(141)
|
Осуществляется рассылка коэффициентов
матриц элементов в общую матрицу [k] всей конструкции.
4. Обработка матрицы системы
производится наложением связей на узлы конструкции. Вычисляется обратная матрица [k]-1.
5. Определяются узловые
перемещения конструкции
|

|
(142)
|
а затем погонные и узловые усилия в
элементах стен, перекрытий и плитном фундаменте Nx, Ny, Тхy, Мх, Му, Мxу.
6. По заданным габаритам
плиты, марке бетона и классу арматуры от действующих изгибающих и крутящих
моментов Мх, Му, Мху, приложенных в уровне срединной
поверхности элементов, исходя из условий прочности, подбираются автоматически
сечения арматуры. Для этого в программе вычисляются характеристики элементов:
расстояния от центров тяжести верхней и нижней арматуры до соответственно нижней
и верхней поверхностей плиты hi, коэффициенты армирования fai прочностные характеристики бетона и арматуры.
7. Для проверки
необходимости армировании верхней и нижней зон определяются для каждой зоны
величины ядровых моментов:
|

|
(143)
|
В случае если расчетное армирование в
верхней и нижней зоне соответственно не требуется, выполняются условия:
|
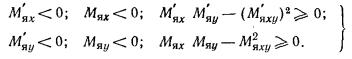
|
(144)
|
Если эти условия нарушаются, производят
подбор арматуры. Предварительно вычисляют величины:

|

|
(145)
|
Различаются следующие случаи:
выполняются условия (144) для верхней
арматуры, но одновременно нарушаются для нижней;
выполняются условия (114) для нижней арматуры, но одновременно нарушаются для
верхней;
одновременно нарушаются условия (144) для
верхней и нижней арматуры.
Условия прочности арматуры нижней зоны
формулируют так:
где
zx, zy - расстояния от оси сечении плиты до центра арматуры;
z0x, z0y - расстояния от оси сечения плиты до оси предельной
сжатой зоны бетона;
Ra - расчетное сопротивление арматуры.
Проверяется выполнение условия |ат
- ая| ≤ 15°, где ат - угол наклона
наиболее опасного вертикального сечения элемента. Для верхней зоны величины

заменяются соответственно на

9. Подбор сечения арматуры проводится
методом последовательных приближений. В качестве примера рассмотрим
последовательность подбора нижней арматуры при условии, что - Мях < 0 и Мяу < 0. Арматура представляется в
виде:
|

|
(149)
|
Подбор частей арматуры проводится методом
последовательных приближений.
В первом приближении определяются значения высот
сжатой зоны, величины zх, zу, zσх, zσу значения 
|
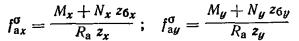
|
(150)
|
Назначается угол ат по величинам ая ,
после чего определяется отношение 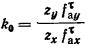
из условия 
Условие (148) преобразуется к виду
 откуда откуда
|

|
(151)
|
Используя выражение (149), определяются
суммарные величины армирования fax и fay.
Затем делается второе приближение, и т.д.
10. После подбора арматуры
анализируется толщина и величина консольных вылетов плиты. Толщина плиты
подбирается из условий продавливания для отдельных колонн и групп колонн по
поверхностям пирамид продавливания. Плита должна удовлетворять требованиям
прочности при любой возможной схеме продавливания. Величины консольных вылетов
проверяются по конструктивным ограничениям.
11. В случаях когда толщина
плиты исходя из условий продавливания недостаточна, программно подбираются
банкетки с толщиной, кратной 300 мм, размерами в плане, кратными 600 мм.
12. Если размеры консолей
малы, вылет консоли принимается большим, кратным 300 мм.
13. Программа выводит на
печать результаты расчета: усилия, перемещения в плите, стенах и перекрытиях,
сечения арматуры плиты, размеры консолей, габариты банкеток. Предусмотрен
графический вывод исходной информации на графопостроитель. Кроме того,
выводится на печать расчетная модель, нумерация узлов, элементов, их
геометрические и физические характеристики.
Пример расчета по программе «Плиска»
Рассчитан плитный фундамент толщиной 1,5
м, бетон марки 200, изображенный на рис. 22. Ребра приняты толщиной 0,3 м,
высотой 1 м, нагрузки в соответствии с рис. 22. Основание моделируется
переменным коэффициентом жесткости. В средней, более широкой части плитного
фундамента жесткость основания 15 МН/м3, в остальных частях 12 МН/м3.
Шаг разбивочной сетки метода конечных элементов в этом примере регулярный -
0,75 × 0,75 м (т.е. в 2 раза чаще, чем это показано на рис. 22).
Исходные данные для расчета записываются
в табличной форме в специальные бланки. На первом бланке описываются реквизиты
объекта: наименование, адрес, шифр, заказчик, дата, а также реквизиты задания:
необходимость учета совместной работы стен и перекрытий, необходимость в
дополнительной автоматической разбивке сетки, форма выдачи на печать расчетной
модели и результатов расчета, требования о графическом выводе информации. На
втором бланке задаются положение разбивочных осей дома в плане и поэтажная
структура. На третьем - координаты углов контура, марка бетона, габариты
фундамента, жесткость основания, а также области переменных свойств основания и
толщины. На четвертом бланке задается положение нагрузок, на пятом - положение
стен и ребер, их толщина и марка бетона.
В результате расчета ЭВМ автоматически
осуществляет нанесение сетки на фундамент и стены, образующей узлы и элементы.
Узлом называется пересечение линий сетки, элементом - пересечение полос
заданной ширины, здесь 0,75 м. Для угловой области плитного фундамента - левой
верхней части (рис. 22) размером 9 × 9 м - принято следующее расположение
элементов: первый расположен в левом верхнем углу (в широкой части плиты у
выреза), затем идут 2, 3, 4-й элемент. Во втором, третьем и четвертом рядах
(сверху вниз) по четыре элемента. Начиная с пятого ряда идут 8 рядов по 12
элементов. Последний элемент в 11-м ряду
имеет номер 112. В пространственной модели для узлов плиты и ребер получены все
линейные и угловые компоненты перемещений, из которых в табл. 72 показаны лишь
вертикальные осадки плиты. Перемещения даны в миллиметрах. Положение узлов на
плите определяется в прямоугольной системе координат с началом, расположенным в
левом верхнем углу прямоугольника, в который вписан плитный фундамент так, что
ось X направлена горизонтально вправо, ось У -
вертикально
Таблица
72
|
Ординаты y, м
|
Абсциссы x, м
|
|
0
|
0,75
|
1,5
|
2,25
|
3,0
|
3,75
|
4,5
|
5,25
|
6,0
|
6,75
|
7,5
|
|
0
|
-
|
-
|
-
|
-
|
30,9
|
30,5
|
30,1
|
29,6
|
29,1
|
28,6
|
28,0
|
|
0,75
|
-
|
-
|
-
|
-
|
30,2
|
29,8
|
29,4
|
29,0
|
28,5
|
28,0
|
27,5
|
|
1,5
|
-
|
-
|
-
|
-
|
29,5
|
29,1
|
28,8
|
28,4
|
27,9
|
27,4
|
26,9
|
|
2,25
|
-
|
-
|
-
|
-
|
28,7
|
28,4
|
28,0
|
28,0
|
27,6
|
26,8
|
26,3
|
|
3,0
|
-
|
-
|
-
|
-
|
27,9
|
27,6
|
27,4
|
27,7
|
27,2
|
26,2
|
25,8
|
|
3,75
|
-
|
-
|
-
|
-
|
27,2
|
27,0
|
26,7
|
27,0
|
26,6
|
25,7
|
25,3
|
|
4,5
|
-
|
-
|
-
|
-
|
26,5
|
26,3
|
26,1
|
26,4
|
26,0
|
25 2
|
24,8
|
|
5,25
|
-
|
-
|
-
|
-
|
25,8
|
25,8
|
25,6
|
25,9
|
25,6
|
24,8
|
24,5
|
|
6,0
|
24,2
|
24,5
|
24,8
|
25,1
|
25,3
|
25,3
|
25,2
|
25,4
|
25,2
|
24,5
|
24,2
|
|
6,75
|
23,7
|
24,0
|
24,3
|
24,6
|
24,7
|
24,8
|
24,8
|
25,0
|
24,8
|
24,3
|
24,0
|
|
7,5
|
23,2
|
23,5
|
23,8
|
24,0
|
24,3
|
24,4
|
24,5
|
24,7
|
24,5
|
24,0
|
23,8
|
|
8,25
|
22,6
|
23,0
|
23,3
|
23,5
|
23,7
|
23,9
|
24,0
|
24,4
|
24,2
|
23,7
|
23,5
|
|
9,0
|
22,2
|
22,5
|
22,8
|
23,0
|
23,3
|
23,5
|
23,6
|
24,0
|
23,9
|
23,4
|
23,2
|
В примере задано вычисление
усилий в плите и ребрах, как в пространственной пластинчатой системе. Для
каждого элемента плитного фундамента компонентами напряженного состояния
являются распределенные (погонные) моменты и поперечные силы, определенные для
центров элементов. В ребрах определены нормальные и касательные напряжения, а
также контактные усилия в местах примыкания к фундаменту. По полученным усилиям
в плитном фундаменте программой осуществляется подбор верхней и нижней арматуры
по направлениям х и у. В табл. 73
приведены значения усилий, уменьшенные в 10 раз, и сечения арматуры в элементах
фундамента. Использованы обозначения:
Nz - распределенный отпор грунта, кПа;
Мх - изгибающий момент относительно оси у,
действующий на сечение с нормалью х, кН·м/м. Положительный момент
вызывает растяжение снизу;
My - изгибающий момент относительно оси х,
действующий на сечение с нормалью у, кН·м/м. Положительный момент
называет растяжение снизу;
Мxy -
крутящий момент, кН·м/м;
Qx - поперечная сила, кН/м, действующая на сечение,
нормальное
оси х. Положительное направление вверх;
Qy - то же, для оси у;
Fax - растянутая арматура по расчету см2/м,
нижняя, вдоль оси х;
Fay - то же, вдоль оси у;
F'ах - растянутая
арматура см2/м, верхняя, вдоль оси x;
F'аy вдоль оси у.
Сжатая арматура по расчету не требуется.
Поскольку в примере не заданы колонны,
продавливание плиты не проверялось. Также не определялись размеры возможных
банкетов. Увеличение консолей по расчету не требуется.
Таблица
73
|
Номер элемента
|
Nz
|
Mx
|
My
|
Mxy
|
Qx
|
Qy
|
Fax
|
Fay
|
F'ax
|
F'ay
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
|
1
|
36,2
|
8,1
|
-2,5
|
2,6
|
26,6
|
-1,0
|
5,5
|
-
|
1,2
|
25,6
|
|
2
|
35,4
|
7,1
|
-3,9
|
4,9
|
21,9
|
8,7
|
11,5
|
-
|
-
|
13,7
|
|
3
|
34,6
|
5,5
|
-22,4
|
1,3
|
17,1
|
41,3
|
2,9
|
0,7
|
-
|
1,2
|
|
4
|
33,8
|
3,6
|
-57,3
|
1,3
|
15,0
|
48,6
|
3,3
|
0,9
|
-
|
2,3
|
|
5
|
36,6
|
35,8
|
-3,0
|
0,4
|
44,7
|
3,0
|
6,6
|
-
|
-
|
21,6
|
|
6
|
35,8
|
43,9
|
7,3
|
9,3
|
80,1
|
-33,8
|
11,3
|
-
|
-
|
11,8
|
|
7
|
35,0
|
38,2
|
-9,8
|
-4,7
|
73,2
|
80,0
|
11,1
|
-
|
-
|
1,0
|
|
8
|
34,3
|
20,5
|
-56,3
|
0,3
|
27,4
|
47,7
|
11,6
|
5,8
|
-
|
-
|
|
9
|
37,0
|
70,2
|
-3,7
|
-4,9
|
50,1
|
7,5
|
6,3
|
-
|
-
|
20,2
|
|
10
|
36,3
|
69,9
|
9,6
|
-1,7
|
-11,3
|
-39,0
|
4,8
|
-
|
-
|
12,6
|
|
11
|
35,5
|
56,1
|
-4,2
|
14,5
|
-27,2
|
77,2
|
22,2
|
3,3
|
-
|
1,6
|
|
12
|
34,7
|
34,1
|
-51,1
|
6,6
|
8,2
|
50,0
|
16,7
|
3,6
|
-
|
-
|
|
13
|
37,4
|
131,7
|
-6,3
|
11,7
|
135,6
|
-13,9
|
12,4
|
-
|
-
|
21,9
|
|
14
|
36,6
|
75,8
|
7,2
|
24,3
|
5,3
|
-18,9
|
10,8
|
-
|
-
|
9,4
|
|
15
|
35,8
|
54,1
|
-0,8
|
16,7
|
18,2
|
37,6
|
41,8
|
8,0
|
-
|
3,2
|
|
16
|
35,1
|
43,9
|
-40,5
|
7,6
|
20,2
|
61,2
|
28,1
|
13,9
|
-
|
2,6
|
|
17
|
36,4
|
18,0
|
13,9
|
17,6
|
57,4
|
-47,6
|
21,2
|
-
|
-
|
20,5
|
|
18
|
35,6
|
15,5
|
42,9
|
25,9
|
40,5
|
-23,7
|
25,8
|
11,8
|
-
|
-
|
|
19
|
34,7
|
13,8
|
32,3
|
25,2
|
36,7
|
53,6
|
11,0
|
9,7
|
-
|
16,7
|
|
20
|
33,8
|
12,6
|
-15,3
|
32,8
|
40,0
|
66,1
|
11,6
|
19,3
|
3,2
|
-
|
|
21
|
32,9
|
10,4
|
-53,9
|
46,7
|
33,2
|
38,0
|
12,0
|
17,7
|
3,5
|
-
|
|
22
|
32,0
|
11,9
|
-72,0
|
59,6
|
31,5
|
10,4
|
14,0
|
5,4
|
6,2
|
14,8
|
|
23
|
31,3
|
19,3
|
-71,4
|
77,5
|
73,8
|
-12,8
|
16,5
|
-
|
12,4
|
29,9
|
|
24
|
30,6
|
45,9
|
-61,8
|
92,0
|
19,9
|
-5,6
|
20,4
|
-
|
16,4
|
39,0
|
|
25
|
37,5
|
109,3
|
-15,8
|
76,3
|
-35,1
|
-83,5
|
29,7
|
2,0
|
18,1
|
45,7
|
|
26
|
36,8
|
96,9
|
34,4
|
52,9
|
30,3
|
-46,3
|
46,2
|
11,6
|
9,7
|
41,1
|
|
27
|
36,1
|
80,6
|
28,5
|
16,8
|
56,2
|
60,7
|
53,6
|
22,8
|
-
|
25,0
|
|
28
|
35,4
|
70,4
|
-28,4
|
3,3
|
53,2
|
81,5
|
36,6
|
20,9
|
-
|
-
|
|
29
|
36,0
|
57,0
|
10,8
|
22,8
|
39,7
|
-28,6
|
18,2
|
-
|
-
|
16,7
|
|
30
|
-35,2
|
75,7
|
59,1
|
38,8
|
127,3
|
-106,6
|
24,8
|
11,8
|
-
|
-
|
|
31
|
34,3
|
71,5
|
47,5
|
12,5
|
124,2
|
137,4
|
17,8
|
9,7
|
-
|
-
|
|
32
|
33,4
|
43,2
|
-25,3
|
31,2
|
36,1
|
64,3
|
27,5
|
23,4
|
-
|
-
|
|
33
|
32,6
|
31,6
|
-63,2
|
43,6
|
21,4
|
35,5
|
19,4
|
15,1
|
-
|
-
|
|
34
|
31,8
|
34,0
|
-80,6
|
53,0
|
22,5
|
11,2
|
20,4
|
5,4
|
-
|
14,8
|
|
35
|
31,1
|
49,6
|
-79,9
|
60,5
|
20,1
|
-10,4
|
19,6
|
-
|
8,5
|
29,3
|
|
36
|
30,6
|
77,6
|
-56,4
|
60,7
|
10,1
|
-59,2
|
22,5
|
-
|
11,7
|
36,9
|
|
37
|
37,6
|
116,8
|
-7,8
|
65,8
|
29,3
|
-78,5
|
29,1
|
-
|
9,9
|
38,4
|
|
38
|
37,0
|
169,4
|
91,4
|
75,7
|
180,7
|
-195,4
|
37,5
|
8,3
|
1,7
|
31,0
|
|
39
|
36,3
|
166,1
|
86,0
|
5,3
|
188,1
|
211,6
|
52,0
|
23,3
|
-
|
18,4
|
|
40
|
35,6
|
110,2
|
-20,9
|
13,8
|
44,8
|
87,2
|
62,9
|
40,8
|
-
|
-
|
|
41
|
36,5
|
64,0
|
9,1
|
16,1
|
-22,2
|
-24,8
|
12,4
|
-
|
-
|
14,0
|
|
42
|
34,7
|
82,4
|
54,4
|
7,9
|
-109,3
|
-102,6
|
11,0
|
11,4
|
-
|
-
|
|
43
|
33,9
|
78,0
|
41,3
|
46,9
|
-107,0
|
137,5
|
17,6
|
8,7
|
-
|
-
|
|
44
|
33,0
|
50,3
|
-31,6
|
40,2
|
-17,7
|
64,0
|
20,8
|
16,2
|
-
|
-
|
|
45
|
32,2
|
39,8
|
-69,4
|
0,9
|
0,4
|
35,2
|
30,0
|
20,8
|
-
|
-
|
|
46
|
31,5
|
42,7
|
-86,0
|
44,5
|
1,4
|
8,3
|
24,9
|
6,6
|
-
|
17,4
|
|
47
|
30,9
|
55,5
|
82,0
|
46,8
|
-3,1
|
20,0
|
18,7
|
-
|
6,2
|
27,0
|
|
48
|
30,4
|
77,1
|
-55,1
|
45,6
|
-12,0
|
-50,0
|
21,8
|
-
|
5,8
|
35,1
|
|
49
|
37,4
|
111,0
|
-3,4
|
37,0
|
-46,1
|
-84,9
|
26,1
|
-
|
5,9
|
34,3
|
|
50
|
36,9
|
163,0
|
99,9
|
14,6
|
-198,7
|
-203,5
|
32,6
|
5,2
|
-
|
23,5
|
|
51
|
36,3
|
162,6
|
96,6
|
66,6
|
-197,6
|
211,9
|
37,4
|
16,0
|
-
|
8,0
|
|
52
|
35,7
|
110,1
|
-12,2
|
41,5
|
-44,0
|
91,5
|
42,6
|
30,7
|
-
|
-
|
|
53
|
34,9
|
41,6
|
8,9
|
20,4
|
-29,4
|
-30,6
|
11,8
|
-
|
1,2
|
14,7
|
|
54
|
34,1
|
33,4
|
28,3
|
21,4
|
-30,0
|
-14,4
|
7,6
|
4,3
|
-
|
-
|
|
55
|
33,3
|
30,3
|
14,0
|
33,1
|
-28,1
|
53,3
|
16,6
|
9,1
|
-
|
2,4
|
|
56
|
32,6
|
32,7
|
-34,0
|
36,5
|
-23,5
|
67,5
|
13,0
|
11,8
|
-
|
-
|
|
57
|
31,8
|
34,4
|
-73,0
|
35,8
|
-11,9
|
38,3
|
19,6
|
14,5
|
-
|
5,9
|
|
58
|
31,2
|
39,2
|
-90,0
|
37,0
|
-9,4
|
7,7
|
19,1
|
3,5
|
3,9
|
19,5
|
|
59
|
30,6
|
49,5
|
-84,2
|
38,1
|
-11,9
|
-23,7
|
17,5
|
-
|
7,2
|
29,3
|
|
60
|
30,1
|
63,3
|
-54,5
|
37,2
|
-20,6
|
-57,6
|
18,6
|
-
|
7,7
|
34,3
|
|
61
|
37,2
|
74,2
|
0,5
|
31,7
|
-42,9
|
-93,8
|
22,0
|
-
|
5,2
|
32,7
|
|
62
|
36,7
|
74,8
|
63,0
|
32,7
|
-51,6
|
-60,9
|
24,0
|
2,0
|
-
|
21,6
|
|
63
|
36,2
|
74,8
|
61,6
|
47,9
|
-51,6
|
64,5
|
29,8
|
13,9
|
-
|
6,8
|
|
64
|
35,6
|
74,0
|
-3,3
|
46,1
|
-43,1
|
97,1
|
25,8
|
22,8
|
-
|
|
|
65
|
34,3
|
32,1
|
7,7
|
31,7
|
3,6
|
-27,3
|
13,7
|
-
|
-
|
13,9
|
|
66
|
33,6
|
24,9
|
25,0
|
30,7
|
7,5
|
12,1
|
21,1
|
14,9
|
-
|
-
|
|
67
|
32,8
|
22,3
|
9,6
|
22,0
|
6,8
|
54,9
|
19,7
|
12,1
|
-
|
7,4
|
|
68
|
32,1
|
24,5
|
-38,9
|
23,0
|
1,6
|
67,5
|
17,14
|
17,2
|
2,8
|
1,7
|
|
69
|
31,4
|
25,5
|
-77,7
|
28,0
|
-12,0
|
37,7
|
12,4
|
8,8
|
-
|
3,8
|
|
70
|
30,7
|
29,3
|
-94,3
|
30,2
|
-17,1
|
7,3
|
11,0
|
-
|
3,0
|
15,0
|
|
71
|
30,2
|
48,5
|
-88,6
|
31,8
|
-17,4
|
-23,0
|
12,7
|
-
|
7,6
|
28,8
|
|
72
|
29,8
|
51,6
|
-56,6
|
35,6
|
-10,9
|
-56,5
|
14,0
|
-
|
8,5
|
34,0
|
|
73
|
36,4
|
62,2
|
58,2
|
47,1
|
18,0
|
-62,5
|
17,1
|
-
|
6,3
|
32,6
|
|
74
|
35,9
|
62,1
|
58,5
|
33,3
|
17,9
|
61,6
|
22,6
|
-
|
2,1
|
25,0
|
|
75
|
35,4
|
61,6
|
"4,0
|
33,2
|
9,7
|
93,6
|
31,3
|
14,0
|
-
|
13,7
|
|
76
|
34,9
|
51,0
|
-58,8
|
37,3
|
-11,5
|
56,3
|
26,2
|
25,2
|
-
|
-
|
|
77
|
33,7
|
34,9
|
5,0
|
33,0
|
-5,7
|
-14,0
|
4,5
|
-
|
-
|
8,1
|
|
78
|
33,0
|
56,7
|
43,7
|
42,3
|
87,0
|
-96,0
|
14,9
|
14,2
|
-
|
|
|
79
|
32,3
|
53,7
|
27,0
|
8,5
|
85,7
|
141,6
|
21,0
|
117
|
-
|
8,6
|
|
80
|
31,5
|
25,3
|
-47,0
|
20,1
|
-4,6
|
63,5
|
23,7
|
20,5
|
-
|
|
|
81
|
30,9
|
13,0
|
-83,8
|
24,4
|
-23,9
|
33,0
|
14,0
|
9,7
|
-
|
-
|
|
82
|
30,3
|
13,2
|
-99,0
|
24,6
|
-26,8
|
7,0
|
10,3
|
-
|
3,1
|
18,0
|
|
83
|
29,8
|
22,5
|
-94,7
|
24,7
|
-26,6
|
-18,7
|
8,1
|
-
|
9,9
|
29,9
|
|
34
|
29,4
|
40,9
|
-69,9
|
28,0
|
-22,0
|
-46,7
|
7,9
|
-
|
10,9
|
34,3
|
|
85
|
36,4
|
72,8
|
-20,0
|
40,0
|
9,9
|
-85,0
|
10,7
|
-
|
8,4
|
32,9
|
|
86
|
36,4
|
123,9
|
85,2
|
65,9
|
161,5
|
-208,3
|
17,3
|
-
|
3,3
|
29,2
|
|
87
|
35,6
|
123,7
|
87,2
|
15,3
|
161,2
|
202,9
|
31,2
|
11,2
|
-
|
14,9
|
|
38
|
35,2
|
72,3
|
-14,3
|
38,4
|
9,7
|
80,7
|
47,1
|
36,8
|
-
|
-
|
|
39
|
33,0
|
7,8
|
2,7
|
19,8
|
-69,5
|
-7,6
|
-
|
-
|
8,0
|
5,3
|
|
90
|
32,3
|
31,2
|
37,8
|
7,0
|
-155,0
|
-93,4
|
-
|
5,5
|
9,7
|
-
|
|
91
|
31,7
|
29,0
|
19,9
|
41,6
|
-151,7
|
-141,0
|
8,5
|
6,9
|
3,7
|
5,3
|
|
92
|
31,0
|
0,4
|
-52,8
|
30,7
|
-61,8
|
60,7
|
9,1
|
10,7
|
-
|
6,7
|
|
93
|
30,3
|
12,3
|
-87,8
|
24,1
|
-44,0
|
31,3
|
21,8
|
18,9
|
3,9
|
24,0
|
|
94
|
29,8
|
-12,8
|
-102,9
|
19,6
|
-42,6
|
8,2
|
7,9
|
-
|
11,3
|
24,9
|
|
95
|
29,3
|
4,1
|
-100,6
|
16,3
|
-44,6
|
-14,3
|
-
|
-
|
12,4
|
27,6
|
|
96
|
29,0
|
14,0
|
-80,1
|
14,8
|
-50,3
|
-39,3
|
-
|
-
|
12,3
|
26,4
|
|
97
|
35,9
|
46,4
|
-35,9
|
13,0
|
-80,8
|
-77,7
|
-
|
-
|
9,6
|
24,2
|
|
98
|
35,6
|
98,3
|
65,7
|
5,9
|
-229,6
|
-206,8
|
5,7
|
-
|
5,5
|
12,8
|
|
99
|
35,2
|
98,3
|
69,8
|
76,9
|
-228,7
|
196,2
|
16,0
|
-
|
-
|
-
|
|
100
|
34,8
|
46,5
|
-24,5
|
66,4
|
-78,7
|
68,7
|
24,3
|
18,6
|
-
|
6,7
|
|
101
|
32,3
|
-51,7
|
0,1
|
15,6
|
-82,3
|
-6,1
|
-
|
-
|
16,2
|
7,0
|
|
102
|
31,7
|
-53,0
|
5,0
|
15,0
|
-77,7
|
-2,6
|
-
|
-
|
18,5
|
-
|
|
103
|
31,0
|
-52,6
|
-13,8
|
27,8
|
-73,6
|
52,6
|
-
|
2,8
|
18,8
|
8,2
|
|
104
|
30,4
|
-50,3
|
-56,6
|
29,6
|
-68,4
|
56,5
|
-
|
4,0
|
18,9
|
6,9
|
|
105
|
29,8
|
-49,8
|
-89,1
|
21,6
|
-53,5
|
32,4
|
-
|
3,6
|
24,1
|
13,6
|
|
106
|
29,2
|
-47,0
|
-105,3
|
14,5
|
-47,8
|
10,9
|
-
|
-
|
19,0
|
20,5
|
|
107
|
28,8
|
-40,3
|
-105,5
|
9,3
|
-50,7
|
-10,5
|
-
|
-
|
18,2
|
25,8
|
|
108
|
28,5
|
-29,9
|
-88,9
|
5,5
|
-63,4
|
-34,4
|
-
|
-
|
17,6
|
27,5
|
|
109
|
35,3
|
-20,1
|
-52,7
|
4,6
|
-88,4
|
-67,0
|
-
|
-
|
14,8
|
26,6
|
|
110
|
35,0
|
-17,9
|
-3,46
|
22,8
|
-93,9
|
-56,0
|
-
|
-
|
10,7
|
21,9
|
|
111
|
34,7
|
-17,0
|
3,0
|
61,4
|
-92,6
|
38,9
|
-
|
-
|
7,4
|
13,0
|
|
112
|
34,4
|
-17,7
|
-34,4
|
76,0
|
-84,7
|
52,6
|
1,5
|
6,0
|
12,5
|
8,1
|
F'ax - растянутая арматура см2, верхняя, вдоль оси x
F'ay - то же вдоль оси y
Сжатая арматура
по расчету не требуется.
Поскольку в
примере не заданы колонны, продавливание плиты не проверялось. Также не
определялись размеры возможных банкетов. Увеличение консолей по расчету не
требуется.
Расчет
фундамента совместно с рамным каркасом
5.54. При отношении длины к ширине здания больше 1,5
допускают использовать одномерную расчетную схему в виде составной балки на
упругом основании (рис. 31).
Нижняя балка с жесткостными характеристиками на изгиб и сдвиг (ЕI1 GF1) моделирует работу плитного фундамента, верхняя балка с
жесткостями EI2,
GF2 заменяет каркас с рамами в продольном направлении.
5.55. Жесткостные характеристики ЕI1 и GF1 определяют по правилам сопротивления материалов. При
этом ЕI1 = DL, где L - ширина
плиты, D - цилиндрическая жесткость,
определяемая по формуле
Приведенные жесткостные характеристики
каркаса определяют по формулам:

где
N -
количество продольных рам;
Fpi - площадь поперечного сечения ригеля i;
ai - расстояние от центра тяжести сечения ригеля i до центра тяжести вертикального сечения всей рамы;
k = n/2, если количество этажей - четная цифра, и k = (n + 1)/2, если - нечетная;
n - этажность здания;
EIpj, EIkj - изгибные жесткости ригелей и колонн j-го этажа;
lр, lk
- длина ригеля и высота этажа.
Приведенную изгибную жесткость здания в
целом определяют по формуле
где
m -
число пролетов продольных рам.

Рис. 31. Расчетная схема каркасного здания
как составной балки
a - расчетная схема; б -
основная система
5.56. Упругие свойства основания характеризуют двумя
параметрами: сср - средним значением жесткостной
характеристики (коэффициента постели) и а - коэффициентом неоднородности
основания, определяемым из условия эквивалентности осадок основания с
переменным коэффициентом постели и упругого полупространства при заданной
нагрузке от сооружения. При этом изменение коэффициента жесткости основания с(х)
относительно середины здания (рис. 32) описывают законом
|

|
(155)
|
5.57. Определение переменного коэффициента жесткости
основания из условия эквивалентности осадок модели Винклера и упругого
полупространства рекомендуют осуществлять в соответствии с указаниями разд.
4 настоящего Руководства.
5.58. В типовом проекте конструкции каркасного здания и
плитного фундамента должны быть рассчитаны на усилия, возникающие в них, при
возведении здания на грунтах с расчетными параметрами основания α = 0,5 (прогиб здания); α = 2 (выгиб); Eср =
150 МПа.

Рис.
32. Изменение коэффициента жесткости основания относительно середины здания
а - выгиб здания; б - прогиб здания
5.59. Осадки каркасного здания определяют по формуле
Коэффициенты y0 и y1 определяют из совместного решения системы уравнений:
Здесь l - половина длины здания; Р2 - приведенная к равномерно распределенной нагрузка на
1 м длины здания.
Реактивный отпор основания определяют по
формуле
|

|
(158)
|
Контактные усилия, действующие между
каркасом и плитой, определяют по формулам.
|

|
(159)
|
|

|
(160)
|
В формулах (159), (160):

Изгибающий момент и поперечную силу, воспринимаемые
зданием, определяют по формулам:
Величины изгибающего момента и поперечной
силы плиты определяют с учетом совместной работы с каркасом по формулам:
|

|
(164)
|
|

|
(165)
|
где
|

|
(166)
|
Величину изгибающего момента,
возникающего в каркасе, вычисляют как разность значений [М] - М1.
Распределение этих усилий между
элементами каркаса производят пропорционально их жесткостям.
Пример расчета плиты совестно с каркасом
Каркасное 9-этажное здание с сеткой
колонн 6 × 6 м рамное в продольном направлении имеет размер в плане (в
осях колонн) 12 × 24 м. Высота этажей 3,3 м. Вертикальная нагрузка,
передаваемая каркасом на плиту (без учета совместной работы), показана на рис.
33. Размеры фундамента - плиты 14 × 26 м, толщина 60 см, марка бетона
300. Изгибная жесткость сечений колонн ЕIk
= 0,6023 × 104 кПа·м4, ригелей ЕIk' = 1,128 104 кПа·м4. Цилиндрическая
жесткость плиты D = 4,864·106 кПа·м4.
Здание расположено на площадке, сложенной
неоднородными грунтами. Упругие свойства грунта характеризуют средней величиной
жесткостной характеристики основания, равной 42500 кН/м3 или на 1 м
плиты сср = 42500·14 =
595·103 кН/м3. Пусть коэффициент неоднородности
основания, определенный из условия эквивалентности осадок упругого
полупространства и модели Винклера с переменной жесткостью основания, α = 0,5.
Требуется определить осадки и усилия в
фундаменте-плите с учетом совместной работы с каркасом.
Нагрузка на 1 м плиты равна:
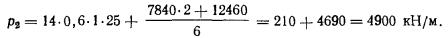
При вычислении обобщенных жесткостных
характеристик жесткости продольных рам суммируют.
С учетом этого

Изгибная жесткость фундамента

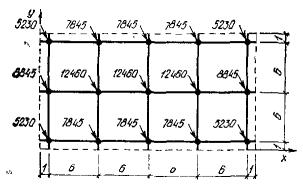
Рис.
33. Вертикальная нагрузка на плиту
Сдвиговую жесткость плиты определяют как
для сплошного тела и принимают равной:

Центр тяжести вертикальных сечений продольных рам
совпадает с центром тяжести сечений ригелей 5-го этажа. Расстояния от центров
тяжести сечений ригелей выше и ниже расположенных этажей будут 3,3; 6,6; 9,9;
13,2 м. С учетом этого приведенная изгибная жесткостная характеристика каркаса

Приведенная вертикальная сдвиговая
жесткостная характеристика каркаса по формуле (153)
равна: 24

Обобщенную изгибную жесткость всего здания с учетом
изгибных и сдвиговых деформаций вычисляют по формуле (154)
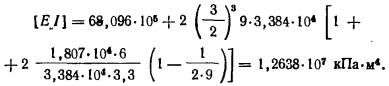
Вычисляют коэффициенты δij -
системы уравнений (157):

Определяют у0 и у1 из решения системы уравнений (157):

Откуда y0 =
0,005967 м, y1 = 0,011
м н уравнение осадок (156) получит вид

Величины обобщенных изгибающего момента и поперечной
силы, воспринимаемых зданием, по формулам (162),
(163) равны:

по середине здания;

на расстоянии l/2 от середины здания.
По формулам (161) определяют величины k2, R и s:

Остальные коэффициенты равны:




Изгибающий момент посередине плиты (х = 0) равен:

Снижение изгибающего момента в плите за счет учета
совместной работы с каркасом составит:

Поперечную силу следует считать полностью
передающейся на плиту.
Учет неупругих деформаций железобетона
5.60. При выполнении расчетов плиты - фундамента каркасного
здания связевой системы допускают приближенный учет неупругих деформаций
железобетона плиты путем определения цилиндрической жесткости в случае
одинакового армирования в двух взаимно перпендикулярных направлениях по формуле
Статический расчет плиты как упругой
системы при этом может выполняться на ЭВМ с использованием одной из программ прил.
1.
В формуле (167) ξ, относительную
высоту сжатой зоны, определяют по формуле
|

|
(168)
|
(если при этом  , то следует
принимать , то следует
принимать 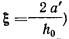 ); z1 - расстояние от центра тяжести площади сечения
растянутой арматуры до точки приложения равнодействующей усилий в сжатой зоне
сечения над трещиной - определяют по формуле ); z1 - расстояние от центра тяжести площади сечения
растянутой арматуры до точки приложения равнодействующей усилий в сжатой зоне
сечения над трещиной - определяют по формуле
|

|
(169)
|
|

|
(170)
|
v -
коэффициент, характеризующий упругопластическое состояние бетона сжатой зоны и
принимаемый равным 0,15 при влажности грунта и воздуха выше 40 % и равным 0,10
при влажности меньше 40 %; b - ширина
сечения; h0 - рабочая высота сечения, равная h - a, где а
-расстояние от равнодействующей усилий в растянутой арматуре до ближайшей грани
сечения; а' - расстояние
от равнодействующей усилий в сжатой арматуре до ближайшей грани сечения; Ra,
Ra.c - расчетные сопротивления рабочей арматуры соответственно
растяжению и сжатию; Fa, F'a
- площадь сечения соответственно
растянутой и сжатой арматуры на единицу длины сечения; Еа - модуль упругости арматуры; Rпр - расчетное сопротивление бетона осевому сжатию.
При неодинаковом армировании в продольном
и поперечном направлениях плиту рекомендуют рассчитывать как ортотропную с
соответствующими каждому направлению жесткостями на изгиб, вычисляемыми по
формуле (167).
Пример расчета плиты с учетом трещин в железобетоне
Плита прямоугольная в плане, постоянной
толщиной h =
20 см из бетона М 200 имеет симметричное,
одинаковое в обоих направлениях армирование. Площадь сечения нижней и верхней
арматуры на 1 м сечения плиты Fa = F'a =15,71 см2. Арматура
класса A-III, Rа = 340 МПа, Еа = 2·105
МПа.
Характеристики бетона: Eб = 2,4·104 МПа, Rпр = 9 МПа
при коэффициенте условия работы 1,1, μб = 0,3. Толщина
защитного слоя равна 3 см. Рабочая высота плиты h0 = h - 3 = 20 - 3 = 17 см.
Вначале вычисляют цилиндрическую
жесткость плиты без учета трещин по формуле (152)

Цилиндрическую жесткость плиты
с учетом трещин вычисляют по формуле (167).
Предварительно определяют ξ и z1,
вследствие того что армирование плиты симметричное и

По формуле (170)

По формуле (167)

После этого расчет плиты может быть
выполнен по одной из программ, приведенных в прил.
1. Подставляя в исходные данные значение D = 1,494·107 Па·м4, получим
результаты упругого расчета плиты; подставляя D = 4,66·106 Па·м4, получим
результаты расчета плиты, приближенно учитывающие влияние неупругих деформаций
железобетона и трещин.
По программе ЦНИИСК-100 на ЭВМ М-222 была
рассчитана железобетонная плита на упругом основании с характеристикой
жесткости грунта 1000 кН/м3. Размер плиты в плане 8 × 8 м,
расчетная сетка 9 × 9 м, под третьим рядом пружин, заменяющих в узлах
сетки упругое основание, задана просадка по 2 см. Нагрузка равномерно
распределенная 10 кН/м2. В результате расчета максимальное значение
изгибающего момента при цилиндрической жесткости D = 1,494·107 Па·м4 получают
равным 351,4 кН·м, а при D = 0,466·106 Па·м4 (вычисленного
с учетом трещин в железобетоне) максимальное значение изгибающего момента
снизилось до 269,5 кН·м, т.е. на 23 %.
Расчет
прямоугольных плитных фундаментов зданий с рамным каркасом при учете жесткости
каркаса и реактивных касательных напряжений
5.61. В рассматриваемой
схеме каркасного здания основными несущими элементами надфундаментного строения
являются колонны и ригели, расположенные в трех взаимно ортогональных
направлениях х, у, z. Они жестко соединены
между собой в узлах и тем самым образуют пространственную рамную систему,
защемленную жестко колоннами нижнего этажа в плитном фундаменте.
5.62. Расчет плитного фундамента при учете влияний
жесткости рамного каркаса и реактивных касательных напряжений выполняют с целью
определения толщины плиты и подбора ее арматуры, удовлетворяющих условиям
прочности и деформаций при учете действительных условий работы сооружения в
целом (плитного фундамента с надфундаментным строением) на упругом основании.
Результаты выполненного по настоящему
разделу расчета позволяют также уточнить величины внутренних усилий в узлах
рамного каркаса и его деформаций, определяемые в практикуемых расчетах рам
каркасных зданий без учета их работ совместно с плитным фундаментом.
5.63. Расчет плитного фундамента при учете жесткости
надфундаментного строения и реактивных касательных напряжений в общем виде
является чрезвычайно сложной биконтактной задачей (т. е. задачей с двумя
контактными поверхностями).
Из-за разнообразия конструктивных решений
каркасных зданий и грунтовых условий в настоящее время нет возможности дать
строгое решение пространственной задачи. В связи с этим допускают использование
приближенного решения, согласно которому влияние жесткости надфундаментного
строения и реактивных касательных напряжений на расчетные величины плитного
фундамента определяют строго в плоской постановке. Затем результаты такого
расчета используют для приближенной оценки влияния указанных факторов на
результаты расчетов по действительной пространственной схеме, выполненных по
существующим методам без учета этих факторов.
5.64. Расчет плитного фундамента с учетом жесткости
надфундаментного строения и реактивных касательных напряжений выполняют по
методу, основанному на расчетной схеме, согласно которой работу рамного каркаса
рассматривают в виде статически эквивалентной сплошной (континуальной) упругой
ортотропной системы с коэффициентом Пуассона vnp = 0 и приведенными модулями деформации (рис. 34):
Епрx, Епрy, Епрz - на растяжение - сжатие, которые определяют с учетом
армировки ригелей и колонн;
Gпрxy, Gпрyz, Gпрzx на
сдвиг которые также определяют с учетом армировки ригелей н колонн.
В приведенном ниже расчете плитных
фундаментов каркасных зданий в плоской постановке за расчетную принята
плоскость xoz (см. рис. 34) и, следовательно, используют лишь следующие
три характеристики упругости указанной ортотропной системы: Епрx, Епрy, Gпрzx контактных условий о равенстве вертикальных и
горизонтальных перемещений соответствующих контактных точек. В случае
рассмотрения аналогичной биконтактной задачи в плоскости yoz в приведенных расчетных формулах следует лишь заменить
индекс х индексом у. В остальном расчет не меняется.
В результате указанного приведения расчет
плитных фундаментов каркасных зданий сводят к решению биконтактной задачи
теории упругости о совместной работе трех континуальных систем - каркаса в воде
статически эквивалентного ортотропного тела, плитного фундамента и упругого
полупространства, где по обеим контактным поверхностям учитывают возникновение
как нормальных, так и касательных реактивных напряжений, которые определяют из
контактных условий о равенстве вертикальных и горизонтальных перемещений
соответствующих контактных точек.

Рис. 34. Схема к расчету плитных фундаментов с учетом
влияния жесткости
надфундаментного строения и реактивных касательных напряжений
5.65. Реактивные напряжения, возникающие по верхней
контактной поверхности плитного фундамента, определяют из условий:
|

|
(171)
|
где
w (x, z = 1), u (x, z = 1) -
соответственно вертикальные н горизонтальные перемещения контактных точек надфундаментного
строения (рамы каркаса), представленного, согласно п. 5.66, в виде статически
эквивалентной континуальной системы;
wф (x), uфв (x) - соответственно
вертикальные н горизонтальные перемещения точек верхней грани плитного
фундамента, определяемые при использовании гипотетических допущений Кирхгофа -
Лява (допущений Бернулли о плоских сечениях).
По нижней контактной поверхности плитного
фундамента удовлетворяются контактные условия:
|

|
(172)
|
где
wф(x), uфв(x) - соответственно вертикальные и
горизонтальны перемещения точек подошвы
плитного фундамента;
w0(x), u0(x) - такие
же перемещения соответствующих контактных точек грунтового основания, рассматриваемого
в виде упругой полуплоскости.
5.66. Напряженно-деформированное состояние надфундаментного
строения, рассматриваемого в виде приведенной континуальной системы, определяют
по теории упругости с использованием разработанного И.И. Гудушаури метода
наложения фиктивных ортотропных систем (метод приведения решений задач теории
упругости к интегрированию обыкновенных дифференциальных уравнений). В
соответствии с этим выражения для величин w (х, z), u (х, z) имеют вид:
|

|
(173)
|
|

|
(174)
|
где первые слагаемые при z = 1 превращаются в нуль, 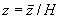 - приведенная к высоте здания
безразмерная вертикальная координата. - приведенная к высоте здания
безразмерная вертикальная координата.
Следовательно, найденными по данному
методу выражениями (173), (174) контактные
условия (171) удовлетворяют точно. Этим методом точное удовлетворение
достигнуто также и для всех остальных граничных условий надфундаментного
строения.
5.67. Напряженно-деформированное
состояние плитного фундамента и контактной поверхности основания определяют с
учетом влияния реактивных касательных напряжений. Пользуясь разработанным И.И.
Гудушаури решением этой контактной задачи, где в качестве внешних воздействий
на плиту принимают найденные по п. 5.66 выражения вертикальных нормальных и
касательных напряжений при z = 1 с обратным знаком, т.е.
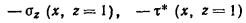
(см. рис. 34), удовлетворения контактных
условий (172) достигают путем нахождения из этих условий постоянных коэффициентов
Аn, Bm полиномов:
|

|
(175)
|
|

|
(176)
|
где
 - приведенная к полуширине плитного фундамента
безразмерная горизонтальная координата; - приведенная к полуширине плитного фундамента
безразмерная горизонтальная координата;
р(х), t(x) - соответственно нормальные и касательные реактивные
напряжения, возникающие по нижней контактной поверхности плитного фундамента.
Tk (x)= cos (k
arccos x) - полином Чебышева первого рода.
5.68. Модель основания,
необходимая для расчета плитного фундамента по п. 5.67, принимают согласно СНиП
на проектирование оснований зданий и сооружений в виде линейно-деформируемого
полупространства с приведенными значениями модуля деформации Eпр0 и коэффициента
Пуассона vпр0.
Значения Eпр0, vпр0 определяют по
предложенным НИИОСП им. Н.М. Герсеванова формулам:
где
ki - коэффициент для i-го слоя, определяемый по табл. 3 прил. 3 главы СНиП
на проектирование оснований зданий и сооружений;
Ei - модуль упругости i-го слоя грунтового основания;
n -
число рассматриваемых слоев грунтового основания;
hi - толщина 1-го слоя грунтового основания.
При этом в выражении (177) рекомендуют
использовать множитель mr,
учитывающий условия работы основания, нагруженного по большой площади, который
определяется по п. 4.17 указанного руководства НИИОСП. Кроме того, используют
корректирующий множитель mЕ, определяемый по п. 6.3 «б» того же Руководства.
5.69. Для надфундаментного
строения значения приведенных модулей деформации при растяжении - сжатии вдоль
осей х, z в случае
пренебрежения влиянием перегородок определяют по формулам:
где
Ех, Еz -
соответственно модули упругости железобетона ригелей и колонн, оси которых
параллельны осям х, z.
Их значения определяют с учетом армировки
по формуле
1 Руководство по
проектированию фундаментных плит каркасных зданий. М., Стройиздат, 1977.
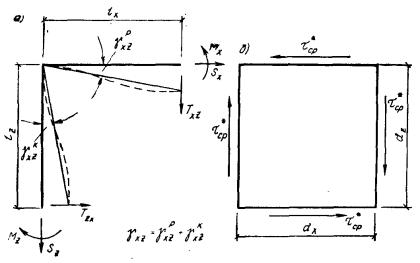
Рис. 35. Схемы для определения приведенного
модуля деформации при сдвиге
а - расчетная ячейка рамы каркасного здания; б - малый элемент континуальной системы надфундаментного строения
каркасного здания
|

|
(181)
|
где
Eа, Еб - модули упругости арматуры и бетона;
Fia, Fiб - площади арматуры и бетона в поперечных сечениях ригеля
или колонны;
lx, ly - расстояния между соседними колоннами вдоль осей х
и у;
lz - высота колони (этажей).
5.70. Для
надфундаментного строения значение приведенного модуля деформации при сдвиге в
случае пренебрежения влиянием перегородок определяют из условия статической
эквивалентности рамы каркаса и рассматриваемой приведенной континуальной
системы на сдвиг. Это условие, составленное для ячейки рамы каркаса (рис. 35,
а) и расположенного в пределах этой ячейки прямоугольного элемента указанной
континуальной системы (рис. 35, б), представляют в виде равенства:
|
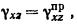
|
(182)
|
где
γx,z -
угол сдвига ячейки рамы каркаса с условно неподвижным узлом, вызванный
действием поперечных сил Тхz = ly lz τ*ср,
Тхz = ly lz τ*ср которые приложены на концах колонны и ригеля;
γпрx,z -
угол сдвига, вырезанного из приведенной
системы элемента.
Из условия
(182) величину Gпрx,z определяют по формуле
где
V = lx ly lz - объем рассматриваемой ячейки рамы каркаса;
Dx, Dz - соответственно жесткости ригеля и колонны на изгиб в
плоскости xoz, определяемые
с учетом армировки по формуле
|

|
(184)
|
где Iб -
момент инерции сечения рассматриваемого элемента (ригеля или колонны).
Выражение (183) не учитывает влияний
перегородок, заполняющих проемы рам каркасных зданий. При учете влияний
перегородок значение величины Gпрx,z значительно увеличивается, что приводит к повышению
экономического эффекта, связанного с учетом жесткости надфундаментного строения
в расчете плитных фундаментов.
5.71. В случае учета влияний перегородок, заполняющих
проемы рам каркасных зданий, значения Eпрx, Eпрy, Gпрx,z, приближенно можно выразить следующими формулами:
где
 - коэффициент, учитывающий влияние наличия
дверных и других проемов в перегородках; - коэффициент, учитывающий влияние наличия
дверных и других проемов в перегородках;
Fi - площадь перегородки с вычетом указанных проемов;
b -
толщина перегородки.
5.72. Расчет плитных фундаментов с учетом жесткости каркаса
и реактивных касательных напряжений, ограничиваясь плоской постановкой задачи,
выполняют на ЭВМ по программе с общим шифром ФКО1. Она составлена на
языках АЛГОЛ-60 и ФОРТРАН-IV.
В этом расчете исходная информация
содержит следующие параметры сооружения:
lx ly - расстояния
между осями соседних колонн, расположенных соответственно вдоль осей х
и у;
1 Шифр ФКО составлен из первых букв слов: фундамент, каркас и основание.
lz - расстояние между осями соседних ригелей (высота
этажа);
Н - высота надфундаментного строения здания;
h = 2 с -толщина плитного фундамента;
L = 2 l - ширина
плитного фундамента;
Eпрx, Eпрy, - приведенные значения модулей упругости при
растяжении (сжатии) вдоль осей х и z континуальной системы надфундаментного строения,
статически эквивалентной заданной рамной системе; их значения определяют по
формулам (179), (180), (185);
Gпрx, -
приведенное значение модуля сдвига для той же континуальной системы,
определяемое по формулам (183), (186);
Eб, Eпр0 - модули упругости бетона и основания, где значение
последнего определяют по формуле (177);
vпр0 -
коэффициент Пуассона основания, определяемый по формуле (178).
5.73. Расчеты на снеговую
нагрузку с интенсивностью q выполняют на ЭВМ с
помощью программы ФКО1. При этом ЭВМ выдает результаты расчета в
виде следующих величин:
1 Шифр ФКО составлен из первых букв слов: фундамент, каркас и основание
а) безразмерные значения
внутренних напряжений приведенной континуальной системы надфундаментного
строения 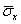 , ,  , ,  в узлах заранее
намеченной сетки (шаги сетки можно брать произвольно, в зависимости от желаемой
густоты узлов), а действительные их значения получают из зависимостей: в узлах заранее
намеченной сетки (шаги сетки можно брать произвольно, в зависимости от желаемой
густоты узлов), а действительные их значения получают из зависимостей:
|

|
(187)
|
б) безразмерные значения
горизонтальных и вертикальных перемещений в указанных узлах (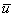 , ,  ), а действительные их значения получают из
зависимостей: ), а действительные их значения получают из
зависимостей:
|
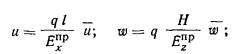
|
(188)
|
в) безразмерные значения
изгибающих моментов  , поперечных
сил , поперечных
сил  и прогибов плитного
фундамента и прогибов плитного
фундамента 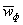 в узлах,
соответствующих указанной выше сетке, а действительные их значения определяют
из зависимостей: в узлах,
соответствующих указанной выше сетке, а действительные их значения определяют
из зависимостей:
|

|
(189)
|
г) безразмерные значения
реактивных нормальных и касательных напряжений под подошвой плитного фундамента
(р{х),
t{x)) в точках, соответствующих
указанной сетке, а действительные их значения определяют из зависимостей:
|

|
(190)
|
5.74. Расчет на
собственный вес и полезную нагрузку, суммарное действие которых представляют в
виде объемного веса γ приведенной
континуальной системы надфундаментного строения, выполняют на ЭВМ с помощью
программы ФКО-2. При этом ЭВМ выдает результаты расчета аналогично п. 5.73. Для
получения же действительных их
значений в данном случае внешнего воздействия используют следующие зависимости:
5.75. Расчет на ветровую
нагрузку с интенсивностью р(z) выполняют на ЭВМ с
помощью программы ФКО-3. При этом ЭВМ выдает результаты расчета аналогично пп. 5.73 и 5.74. Для получения же действительных их значений в
данном случае внешнего воздействия используют следующие зависимости:
5.76. Расчет плитных фундаментов на снеговую нагрузку с
приближенным учетом влияний жесткости каркаса и реактивных касательных напряжений
по пространственной схеме выполняют в такой последовательности: выполняют
соответствующий расчет сначала любым практикуемым методом, разработанным по
пространственной схеме без учета указанных факторов; затем определяют
коэффициенты перехода, выражающие влияние жесткости надфундаментного строения и
реактивных касательных напряжений на результаты расчета, путем деления значений
расчетных величин, полученных по программе ФКО-1 с учетом влияний указанных
факторов и без их учета. Окончательные результаты расчета получают путем
перемножения коэффициентов перехода на значения расчетных величин, полученных
по пространственной схеме без учета перечисленных факторов.
5.77. Расчет
плитных фундаментов на собственный вес, полезную и ветровую нагрузки с
приближенным учетом влияний жесткости каркаса и реактивных касательных
напряжений по пространственной схеме выполняют аналогично п. 5.76, используя
вместо ФКО-1 соответственно программы ФКО-2 и ФКО-3.
5.78. Полученные по пп. 5.73, 5.74 и 5.75 результаты используют и для расчета рам каркасных
зданий с учетом совместной работы надфундаментного строения и плитного
фундамента, по контактной поверхности которого возникают и касательные
реактивные напряжения. Для этого от приведенной континуальной системы
надфундаментного строения возвращаются обратно к действительной рамной системе.
Из приведенной континуальной системы рассматривают элемент формы прямоугольной
призмы размерами lx, ly, lz, на гранях которого прикладывают найденные из расчетов
по пп. 5.73, 5.74 и 5.75 значения внутренних напряжений σх, σz, τ*. Путем соответствующего интегрирования
указанных напряжений в пределах граней рассматриваемой призмы определяют усилия
во всех элементах (колоннах и ригелях), входящих в этот узел.
Таким образом, получают эпюры изгибающих
моментов, поперечных сил и осевых сил рамы с учетом ее работы совместно с
плитным фундаментом.
Так, например, в элементах внутренних
узлов рамы каркаса усилия определяют, пользуясь приведенными на рис.
36 двумя схемами, первая из которых а - призматический элемент
(размерами lx, ly, lz) приведенной континуальной системы, на гранях которой
прикладывают найденные в расчете по п.
5.73 напряжения, а второй б - соответствующий указанному
призматическому элементу узел рамы каркаса с искомыми усилиями.
Исходя из этих схем, искомые усилия в
произвольном узле i с координатами xi, zi определяют с помощью формул:
а) усилия в середине пролета левого
ригеля узла i:
С помощью найденных по формулам (198) -
(200) значений определяют усилия рассматриваемого ригеля в самом узле i. При этом значения Sрл, Трл не меняются, а
изгибающий момент находят из выражения
|
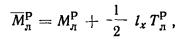
|
(201)
|
где Трл, Мрл
- найденные по формулам (199), (200) значения поперечной силы и изгибающего
момента в середине пролета рассматриваемого ригеля;
б) выражения усилий правого
ригеля узла i отличаются
от выражений (198) -(200) лишь тем, что в их подынтегральные функции вместо
аргумента  входит
аргумент входит
аргумент  ; ;
в) усилия в середине верхней
стойки узла i рамы определяют с помощью формул:

Рис. 36. Схемы для
определения усилий в элементах внутренних узлов рамы каркасных зданий по
найденным напряжениям в приведенной континуальной системе
a - эпюры найденных напряжений; б - усилия в элементах i-го узла каркаса
Найденные по
формулам (202), (203) усилия Ncв, Тcв будут действовать и в сечениях у
самого узла i. А изгибающий момент рассматриваемой стойки в узле i определяют по формуле
|

|
(205)
|
где
Тcв,
Mcв - найденные по формулам (203), (204) значения поперечной силы и изгибающего момента в
середине рассматриваемой стойки;
г) выражения усилий нижней стойки узла i отличаются
от выражений (202) - (204) лишь
тем, что в их подынтегральные функции вместо аргумента  входит аргумент входит аргумент  . .
Аналогично определяют усилия в элементах крайних
узлов рамы каркаса. Разница лишь в том, что при этом используют соответствующие
схемы вместо приведенных на рис. 36 схем.
Пример расчета напряженно-деформированного состояния плитного
фундамента с учетом реактивных касательных напряжений и жесткости надфундаментного
строения
Требуется выполнить расчет плитного
фундамента, когда на обеих (верхней и нижней) его контактных поверхностях
действуют как нормальные, так и касательные реактивные напряжения.
Расчет выполняют по пп.
5.61 - 5.78.
За модель основания принята упругая
полуплоскость с модулем деформации Е0 = 12000 МПа и с коэффициентом Пуассона v0 =0,3.
Марка бетона плитного фундамента М 200 с
модулем упругости Еб = 24000 МПа. Ширина плитного фундамента L = 2l = 30 м, толщина фундамента h = 2с = 1,5 м;
Надфундаментное строение - рама
20-этажного каркасного здания.
Геометрические и физические
характеристики колонн: сечения колонн всех этажей принимаются одинаковыми
(программы ФКО составлены для более общего случая, когда сечения колонн
меняются по высоте линейно); размеры их поперечных сечений 60 × 60 см;
площадь поперечного сечения арматуры FKа = 90 см2; модули
упругости бетона (М 200) и арматурной стали соответственно EKб = 24000 МПа, EKa = 200000 МПа.
Геометрические и физические
характеристики ригелей: площадь поперечного сечения 50 × 40 см; площадь
поперечного сечения арматурной стали FPа = 50
см2; модули упругости бетона (М 200) и арматурной стали
соответственно EPб = 24000 МПа,
EPa = 210000 МПа.
Во всех случаях коэффициент Пуассона
бетона vб = 0,17.
Рассматривается частный случай, когда на
здание действует равномерно распределенная снеговая нагрузка с интенсивностью q. Расчет выполняют на ЭВМ с
помощью программы ФКО-1.
Модули упругости ригелей и колонн в соответствии с п.
5.69 равны:


Рис. 37. Некоторые результаты расчета
плитного фундамента
а - расчетная схема; б - эпюры реактивных касательных напряжений; в - эпюры реактивных нормальных
напряжений; г - эпюры
изгибающих моментов; д - эпюры
поперечных сил; е - эпюры
относительных прогибов
Для
надфундаментного строения в случае пренебрежения влиянием перегородок значения
приведенных модулей деформации при растяжении
- сжатии вдоль осей х и z и модуль сдвига в соответствии с пп.
5.69, 5.70
соответственно равны:

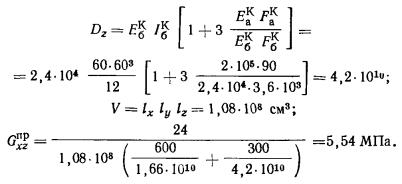
На рис. 37 даются некоторые результаты
расчета плитного фундамента с учетом реактивных касательных напряжений и жесткости
надфундаментного строения.
5.79. В рассматриваемой схеме связевого каркаса основными
несущими элементами надфундаментного строения являются: система колонн (стоек),
горизонтальные диски - перекрытия и диафрагмы жесткости.
5.80. Расчет плитного фундамента здания со связевым каркасом
при учете реактивных касательных напряжений выполняют в следующей
последовательности:
а) по существующему методу
расчета, разработанному без учета реактивных касательных напряжений, определяют
максимальные значения изгибающих моментов и прогибов плитного фундамента ( ), ( ), ( ) )
б) по рис. 38 и 39 для
заданных значений отношений толщины плиты к ее ширине или длине ( ) и модуля деформации основания к модулю деформации бетона
плиты ) и модуля деформации основания к модулю деформации бетона
плиты  , находят значения коэффициентов Rm и Rw; , находят значения коэффициентов Rm и Rw;
в) расчетные значения
изгибающих моментов и прогибов плитных фундаментов зданий со связевым каркасом
при учете реактивных касательных напряжений определяют по формулам:
|

|
(206)
|
|

|
(207)
|
где
 , ,  , - определяются любым из практикуемых методов расчета
плитных фундаментов, разработанных по пространственной схеме; , - определяются любым из практикуемых методов расчета
плитных фундаментов, разработанных по пространственной схеме;
Rm, Rw - безразмерные коэффициенты перехода, с помощью
которых учитывают влияние реактивных касательных напряжений.

Рис.
38. Коэффициент перехода Rм

Рис.
39. Коэффициент перехода Rw
Пример расчета напряженно-деформированного
состояния
плитного фундамента со связевым каркасом на упругом основании с учетом
реактивных касательных напряжений
Для оценки влияния реактивных касательных
напряжений на результаты расчета плитных фундаментов дается его расчет по
методу, разработанному И.И. Гудушаури (с учетом реактивных касательных
напряжений) и по методу П.И. Клубика, разработанного без учета этого фактора.
Рассматривают плитный фундамент,
нагруженный равномерно распределенной нагрузкой с интенсивностью q.
Расчет выполнен для частного случая,
когда  , где Е0, Eб - соответственно модули упругости основания и бетона
плитного фундамента. , где Е0, Eб - соответственно модули упругости основания и бетона
плитного фундамента.
На рис. 40 даются эпюры безразмерных
величин прогибов  и изгибающих моментов и изгибающих моментов 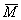 плитного фундамента, полученных с
учетом и без учета влияний реактивных касательных напряжений. плитного фундамента, полученных с
учетом и без учета влияний реактивных касательных напряжений.
5.81. Расчет толстых
плитных фундаментов выполняют на заданные внешние воздействия с целью
определения толщины плиты и подбора арматуры (с их распределением в теле
плитного фундамента) из условий прочности и деформаций. Такой расчет выполняют
по теории упругости при точном удовлетворении всех граничных условий. По
вертикальным граням плитного фундамента нормальные и касательные напряжения
равны нулю. По верхней грани плитного фундамента касательные напряжения равны
нулю, а нормальные напряжения равняются внешней нагрузке, если она
распределенная, или же нулю, если она сосредоточенная. Если на плитный
фундамент вертикальная нагрузка приложена в виде множества сосредоточенных сил,
ее приводят к статически эквивалентной распределенной нагрузке. По подошве
плитного фундамента нормальные и касательные перемещения соответствующих
контактных точек плитного фундамента и основания (упругого полупространства)
тождественно равны.
5.82. Для оценки погрешности расчета толстых плитных
фундаментов, рассматриваемых как тонкие, следует использовать приведенные ниже
указания

Рис. 40. Результаты расчета плитного
фундамента с учетом реактивных касательных напряжений
а - эпюры прогибов w при k = 0,l и α = 0,05; 0,1; 0,15; 0,2; 0,25; 0,3
сплошные линии соответствуют t ¹ 0, пунктирные – t = 0; б - эпюры изгибающего моменты  при k = 0,1 и α = 0,05; 0,1; 0,15; 0,2; 0,25;
0,3 при k = 0,1 и α = 0,05; 0,1; 0,15; 0,2; 0,25;
0,3
5.83. Расчет толстых балочных плитных фундаментов при
строгом удовлетворении всех граничных условий, указанных в п. 5.81 (рис. 41), а
именно:
при
|

|
(208)
|
при
|

|
(209)
|
при
|

|
(210)
|
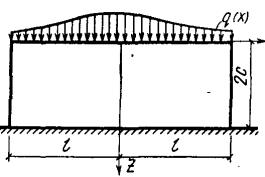
Рис. 41. Схема расчета
толстых плитных фундаментов на упругом полупространстве в плоской постановке
выполняются по теории упругости при
использовании метода наложения фиктивных ортотропных систем, разработанного
И.И. Гудушаури. При этом в качестве модели основания принимают упругую
полуплоскость с упругими характеристиками Епр0, vпр0,
определяемыми согласно п.
5.68.
5.84. Расчет толстых балочных плитных фундаментов (рис. 41)
с удовлетворением точно граничных условий (208) - (210) выполняют
на ЭВМ по программе с шифром ТФП1. Она составлена на языках АЛГОЛ-60
и ФОРТРАН-IV.
При расчете толстых плитных фундаментов
(рис. 41) по программе ТФП ЭВМ выдает результаты расчета в виде напряжений и
перемещений для произвольного количества (заранее намеченного) точек:
а) безразмерные значения
внутренних напряжений  , ,  , ,  , действительные значения которых определяют из
зависимостей: , действительные значения которых определяют из
зависимостей:
|

|
(211)
|
б) безразмерные значения
горизонтальных и вертикальных перемещений указанных точек плиты 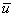 и и  , действительные значения которых определяют из
зависимостей: , действительные значения которых определяют из
зависимостей:
|

|
(212)
|
|
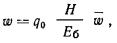
|
(213)
|
где
q0 = q (x = 0); L = 2l - длина
балочного плитного фундамента.
1 Шифр ТФП составлен из первых букв слов: толстый, фундамент и плита

Рис.
42. Сопоставление эпюр горизонтальных нормальных напряжений, построенных для
поперечных сечений плиты при α = 1/3; k = 0,2; сплошные линии
соответствуют расчету по теории упругости, а пунктирные линии – расчету с
использованием гипотезы Бернулли при учете реактивных касательных напряжений

Рис.
43. Сопоставление эпюр горизонтальных нормальных напряжений σх, построенных
для поперечных сечений фундаментной плиты при α = 0,2; k = 1; сплошные линии
соответствуют расчету по теории упругости, а пунктирные линии - расчету с
использованием гипотезы Бернулли при учете реактивных касательных напряжений.
Пример расчета напряженно-деформированного состояния
толстого плитного фундамента на упругом полупространстве по теории упругости
(т.е. без гипотезы Бернулли) с учетом реактивных касательных напряжений
Расчет выполняют по пп.
5.81 - 5.84.
Задачу рассматривают в плоской постановке. В качестве модели основания
принимается упругая полуплоскость. Приведенные ниже результаты численных
примеров расчета плитных фундаментов получены для следующих характеристик:
Eб = 24000 МПа -модуль упругости бетона;
vб = 0,17 - коэффициент Пуассона для бетона;
E0 = 12000
МПа -модуль упругости основания.
На плитный фундамент действует равномерно
распределенная нагрузка с интенсивностью q.
Расчет выполнен по указаниям пп.
5.81 - 5.84
на ЭВМ по программе ТФП для различных значений 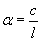 , где l,
с -полуширина и полутолщина плитного фундамента. , где l,
с -полуширина и полутолщина плитного фундамента.
На рис. 42, 43 даются сопоставления эпюр
горизонтальных нормальных напряжений σх, полученных по теории
упругости и с использованием гипотезы Бернулли при учете реактивных касательных
напряжений.
На рис. 44 даются сопоставления эпюр
прогибов, полученные по трем различным методам: по теории упругости; при
использовании гипотезы Бернулли, когда учитываются реактивные касательные
напряжения; при использовании гипотезы Бернулли без учета реактивных
касательных напряжений.

Рис. 44. Сопоставление прогибов плитного
фундамента, полученных при k = 1; α = 0,2 по трем различным способам
1 - по теории
упругости, т.е. без использования гипотезы Бернулли; 2 - при использовании
гипотезы Бернулли, касательных напряжений (t ¹ 0); 3 – при
использовании гипотезы Бернулли и принимая t = 0.
5.85. Расчет рекомендуют как проверочный для контроля достаточности площади арматуры
плитного фундамента по условиям работы в стадии разрушения, выполняют после
предварительного выбора марок бетона и арматуры, назначения высоты плиты из
условия прочности на продавливание.
5.86. Метод может быть использован в двух вариантах
расчета:
первый - при заданной площади
арматуры определяется соответствующее максимальное давление на основание из
условий работы плиты в стадии разрушения;
второй - при заданном среднем давлении на
основание определяется площадь арматуры по условиям работы плиты в стадии
разрушения.
5.87. Фундаментную плиту рассматривают как статически
неопределимую конструкцию на грунтовом основании, в которой под действием
нагрузок от колонн образуются линейные упругопластические шарниры, разделяющие
плиту на кинематические звенья. К таким плитам применяют все основные положения
расчета железобетонных плит фундаментов по кинематическому методу теории предельного
равновесия. В предельном состоянии плиты устанавливается предельное равновесие
внешних и внутренних усилий, которые формируются в результате развития
упругопластических деформаций в грунте основания и в железобетонной
фундаментной конструкции.
5.88. В расчетах
плитных фундаментов под сетку колонн возможны две схемы излома при разрушении:
перекрестная (рис. 45) и полосовая (рис. 46).
|

|

|
|
Рис. 45.
Среднее поле плитного фундамента каркасного здания с квадратной сеткой колонн
а - перекрестная схема излома при разрушении, б - разрез плитного фундамента
|
Рис.
46. Среднее поле плитного фундамента каркасного здания с неквадратной сеткой
колонн
а -полосовая схема излома при разрушении, б - разрез плитного фундамента
|
5.89. При перекрестной схеме излома, имеющей
место в плитном фундаменте каркасного здания с квадратной сеткой, расчет
фундамента производится по следующей формуле:
|

|
(214)
|
где р - среднее давление на основание, МПа;
Мп = F'а h0 - пролетный момент, Н·м;
Моп = Fа h0 - опорный момент, Н·м;
Fa - площадь
сечения нижней арматуры, м2;
F -
площадь сечения арматуры, м2;
h0 -
полезная высота фундаментной плиты, м;
l -
расчетный пролет, соответствующий расстоянию между разбивочными осями, м;
kσ - коэффициент, учитывающий концентрацию реактивных
давлений под подколонной частью плиты в зависимости от отношения l/hп (табл. 74);
Таблица 74
|
l/hп
|
3
|
5
|
7
|
9
|
11
|
|
kσ
|
1
|
0,8
|
0,7
|
0,67
|
0,64
|
|
kτ
|
0,08
|
0,06
|
0,04
|
0,02
|
0,00
|
hп - высота плиты, м;
kτ - коэффициент, учитывающий разрушающее действие
касательных напряжений по подошве плиты, принимаемый равным нулю для
водонасыщенных глинистых грунтов; по табл. 74 с коэффициентом 0,5 - для влажных
глинистых грунтов и по табл. 74 - для остальных грунтов.
5.90. При полосовой схеме излома, характерной для плитных
фундаментов с неквадратной сеткой колонн или несущими стенами, расчет плиты
производится по формуле
|

|
(215)
|
где
lp = 1,1 lп - расчетный пролет, м;
lп -
расстояние между внутренними гранями подколенников, м;
Lп - длина
плиты или участка, для которого производится расчет, м.
Остальные обозначения те же, что и в
формуле (214).
5.91. При неквадратной сетке колонн расчет арматуры по
меньшему пролету производится тоже по формуле (215), при этом за lп
принимается расстояние между внутренними гранями подколенников в направлении
меньшей стороны сетки.
5.92. После расчета по кинематическому методу проверяют
ширину раскрытия трещин в фундаменте. При необходимости либо увеличивается
площадь арматуры, либо уменьшается внешняя нагрузка на фундамент, и расчет
повторяется.
5.93. Уменьшение площади арматуры по предлагаемому методу
должно быть не более как на 15-20 % по сравнению с любым методом, основанным на
упругом характере работы железобетона.
ПРИМЕР
Требуется определить сечение рабочей
арматуры Fa и F'a класса
А-II (Rа = 270 МПа) плитного фундамента с нагрузкой по сетке
колонн 3 × 4,5 м, лежащего на песчаном основании с р = 0,3 МПа.
Задаемся соотношением рабочей арматуры . Fa = 1,8 F'a. По табл. 74
для песчаных грунтов при l/hп = 4,5/0,5 =
9 находим

В рассматриваемом случае при неквадратной сетке
колонн принимаем полосовую схему излома фундамента по пролету, равному 4,5 м, и
выполняем расчет арматуры по формуле (215)

Находим  Принимаем на 1
м сечения плитного фундамента верхнюю арматуру 5 Ø 16 А-II и нижнюю 5 Ø 20 A-II. Принимаем на 1
м сечения плитного фундамента верхнюю арматуру 5 Ø 16 А-II и нижнюю 5 Ø 20 A-II.
По пролету 3 м расчет арматуры производим
так же по формуле (215), как для полосовой схемы излома плиты.
5.94. Указания раздела относятся к расчету плитных
фундаментов полигонального очертания в плане постоянной либо
ступенчато-переменной толщины при действии произвольной нагрузки с учетом и без
учета влияния жесткости силосных корпусов.
5.95. При расчете плиты принимаются следующие допущения:
деформации плиты описываются
уравнениями технической теории тонких изгибаемых пластин (теория Кирхгоффа)
либо пластин средней толщины (теория Рейсснера);
плита изотропная, материал плиты и
основания линейно-упругий;
при наличии ребер плита считается
конструктивно анизотропной;
вертикальные перемещения точек плиты и
основания одинаковы;
силы трения между плитой и основанием
отсутствуют.
5.96. Расчет плиты производится на следующие типы нагрузок
и воздействий:
равномерно распределенные по прямоугольной
площадке вертикальные нагрузки;
сосредоточенные по линии погонные
вертикальные силы и моменты;
сосредоточенные в точках вертикальные
силы;
нагрузки, приходящиеся на верхнее
строение;
смещения опертых краев плиты и повороты в
заделках.
5.97. Для основания следует использовать расчетную схему,
характеризуемую переменным коэффициентом жесткости, либо в виде
линейно-деформируемого слоя, приближенно описываемого двумя коэффициентами
жесткости (см. разд.
1).
5.98. При наличии жесткого верхнего строения (силосный
корпус, соединяемый с плитой системой упругодеформируемых стоек) производится
совместный расчет плиты и жесткого верхнего строения.
5.99. Расчет фундаментной плиты по указаниям настоящего
раздела допускает учет наличия свайного поля с дискретным расположением свай в
расчетной схеме, для чего должны быть заданы информация о расположении свай и
характеристики податливости свай (смещение оголовка сваи в вертикальном
направлении от действия единичной силы, угол поворота оголовка сваи от действия
единичного момента).
5.100. Для расчета плитного фундамента рационально
использовать метод конечных элементов в варианте метода перемещений.
Потенциальная энергия системы «плита +
основание» представляется в виде зависимости (56).
Выражение для потенциальной энергии
деформации изгибаемой плиты Uп, входящей в
формулу (56), зависит от принятых гипотез,
используемых при выводе разрешающих уравнений изгиба плиты. Для тонких
анизотропных плит (теория Кирхгоффа) это выражение имеет вид
|
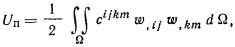
|
(216)
|
где
Ω -
область плоскости (х, у),
занимаемая плитой;
cijkm - компоненты тензора
анизотропии;
w - функция прогибов (перемещений) плиты.
Здесь и далее нижними индексами после
запятой помечаются производные, взятые по соответствующей координате, например:

В формуле (216) и далее используется
соглашение о суммировании по повторяющимся индексам. Все индексы пробегают
значения от 1 до 2, причем 1 соответствует направлению вдоль оси х, а 2 - вдоль оси у.
В случае изотропной плиты
|
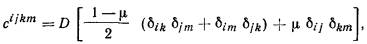
|
(217)
|
где
 - цилиндрическая жесткость плиты при изгибе; - цилиндрическая жесткость плиты при изгибе;
Е - модуль упругости материала плиты;
h - толщина плиты;
μ - коэффициент
Пуассона;
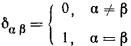 - символ Кронекера. - символ Кронекера.
Выражение для Uп в случае
изотропной плиты имеет вид
|

|
(218)
|
Для изотропных плит средней толщины
(теория Рейсснера) выражение для Un записывается в виде

где помимо уже введенных обозначений
положено
|

|
(219)
|
причем φx, φy -
углы поворота нормали к срединной поверхности плиты относительно осей у и х соответственно. Положительные направления перемещения w и поворотов φx и φy показаны на рис. 47.

Рис.
47. Положительные направления перемещения w и углов поворота φx, φy
Для тонких плит (теория Кирхгоффа)
имеют место соотношения:
|

|
(220)
|
Выражение для Uо зависит от
принимаемой расчетной схемы основания. Для основания с двумя коэффициентами
постели Uо имеет вид
|

|
(221)
|
где
Ωе -
область плоскости (х, у)
внешняя к области Ω, т. е. Ωе есть
дополнение Ω до всей плоскости (х, у).
Интеграл по Ωе в
выражении (221) учитывает работу основания за пределами плиты. В случае
основания, описываемого переменным коэффициентом жесткости, в выражении (221)
пропадает интеграл по Ωе и, кроме того, полагается С2 = 0.
Падение потенциала внешних сил (работа
внешних сил на статически соответствующих им перемещениях) определяется
выражением
|

|
(222)
|
где
q(x, у) - распределенная по площади нормальная к срединной
поверхности плиты нагрузка;
g(s) - погонная, распределенная по линии нагрузка;
Pi - сосредоточенная сила,
действующая на плиту в точке с координатами (хi, уi);
m(s) -погонный, распределенный по линии момент;
Mxi, Мyi - сосредоточенные моменты относительно осей х и у, соответственно
действующие на плиту в точке с координатами хi, уi;
φп - угол поворота нормали к срединной поверхности плиты
вокруг оси s.
Положительные направления действующих на
плиту нагрузок показаны на рис. 48.

Рис. 48. Положительные направления
действующих на плиту нагрузок
При решении задачи по методу конечных
элементов исходная континуальная задача минимизации функционала полной
потенциальной энергии системы приближенно заменяется дискретной задачей,
решение которой сводится к решению системы линейных алгебраических уравнений,
т. е. система с бесконечным числом степеней свободы заменяется системой с
конечным числом степеней свободы. Процедура дискретизации заключается в том,
что вся область интегрирования представляется в виде объединения
непересекающихся областей:
|

|
(223)
|
Отдельная область интегрирования Ωr составляет при этом так называемый «конечный»
элемент. При этом
|

|
(224)
|
где
Ur - полная потенциальная энергия, накапливаемая в
отдельном конечном элементе, причем
|

|
(225)
|
В пределах конечного элемента прогиб w аппроксимируется линейным агрегатом вида
|

|
(226)
|
где функции  определены только на r-м
элементе. Параметры αi выражаются через перемещения и некоторое количество
производных от перемещения в узловых точках конечного элемента. В случае плит
средней толщины принимается независимая аппроксимация прогибов и углов
поворота. определены только на r-м
элементе. Параметры αi выражаются через перемещения и некоторое количество
производных от перемещения в узловых точках конечного элемента. В случае плит
средней толщины принимается независимая аппроксимация прогибов и углов
поворота.
Используя результаты подстановки в
формулу (226) значений αi,
выраженных через узловые перемещения, по формуле (225) получаем
|

|
(227)
|
где
Rr - матрица жесткости конечного элемента;
Rpr - грузовой вектор;
Zr - вектор узловых перемещений конечного элемента, размерность которого
определяется числом степеней свободы этого конечного элемента, причем
где
Rrп - матрица жесткости конечного элемента плиты;
Rro - матрица жесткости соответствующего конечного
элемента упругого основания.
Полная потенциальная энергия дискретной
системы принимает вид
|
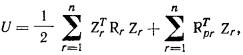
|
(229)
|
где
n -
общее количество конечных элементов.
Из условия минимума полной потенциальной
энергии системы в положении равновесия получается дискретное разрешающее
уравнение в виде
|

|
(230)
|
где
К - полная матрица жесткости системы;
Кp - полный грузовой вектор;
Z -
вектор обобщенных перемещений всех узлов системы.
Матрица жесткости К набирается суммированием из элементов матриц жесткостей Rr
отдельных конечных элементов, причем в каждом узле системы суммируются
компоненты матриц Rr, относящихся к элементам, сходящимся в данном узле.
Например, для узла k на рис. 49
компоненты соответствующего блока матрицы К
набираются суммированием из компонентов матриц R3, R7, R10, R11. Аналогично компоненты полного грузового вектора Кр набираются суммированием
из элементов векторов Rpr.

Рис. 49. Конечные элементы, сходящиеся в узле u
5.101. Для расчета
плит с учетом влияния верхнего строения следует использовать смешанный метод расчета.
При этом вводятся следующие
предпосылки:
верхнее строение рассматривается в
расчетной схеме как твердое недеформируемое тело;
верхнее строение соединяется с плитой
системой упругодеформируемых стоек;
стойки верхнего строения обладают
конечной жесткостью на сжатие и изгиб и не сопротивляются закручиванию.
5.102. Основная
система смешанного метода расчета образуется отделением верхнего строения
(вместе со стойками) от плиты и наложением дополнительных связей на верхнее
строение, устраняющих жесткое его смещение. Неизвестными смешанного метода
расчета являются усилия в стойках верхнего строения и перемещения наложенных
связей.
5.103. Окончательные результаты расчета плиты получаются
суммированием величин, получаемых от действия внешних нагрузок и от усилий,
передающихся от стоек верхнего строения.
Пример расчета плитного
фундамента силосного корпуса по программе КОРПУС-ЕС.
Требуется выполнить расчет прямоугольного
в плане плитного фундамента, лежащего на сжимаемом основании. Жесткое верхнее
строение соединено с фундаментом стойками, центры которых показаны на рис. 50.

Рис.
50. Плитный фундамент силосного корпуса
К заштрихованной части фундамента
приложена равномерно распределенная нагрузка с равнодействующей Q = 2000 кН.
На верхнее строение действует центральная нагрузка Тz = 10000 кН.
Характеристики материала фундамента
приняты равными: модуль упругости бетона Еб
= 26500000 кПа; толщина фундамента h = 1 м; коэффициент Пуассона бетона v = 0,167.
Для основания фундамента задан постоянный
коэффициент жесткости (постели) k = 2470 кН/м3.
Стойки высотой hс =
12,8 м характеризуются осевой жесткостью EF = 28350000 кПа·м2.
Расчет производим для 1/4
части фундамента (рис. 51), учитывая симметрию конструкции и заданной нагрузки.
Разбивка фундамента конечно-элементной сеткой показана на рис. 51.

Рис.
51. Схема разбивки плитного фундамента на конечные элементы
Расчет выполнен на ЭВМ ЕС-1022 по
программе КОРПУС-ЕС. Информация к расчету описана на языке ВХОД (диалект
КОРПУС). В табл. 75 приведены результаты расчета в узлах 13-18 для двух вариантов загружений:
1 - нагрузка Q приложена к плитному фундаменту;
2 - нагрузка Тz приложена
к силосному корпусу.
Таблица
75
|
Узел сетки
|
Координаты
узлов сетки, м
|
Загружение
|
Осадка
w, см
|
Изгибающие
моменты на 1 м сечения Н, кН·м/м
|
Крутящий
момент на 1 м сечения Н, кН·м/м
|
Отпор основания р, кПа
|
|
х
|
у
|
Mx
|
Му
|
|
13
|
2,0
|
0,0
|
1
2
|
1,84
1,12
|
-343,0
-1,4
|
184,4
33,9
|
35
-3,4
|
45,5
27,7
|
|
14
|
2,0
|
1,0
|
1
2
|
1,83
1,12
|
-391,7
24,8
|
206,7
18,0
|
156,5
-34,8
|
45,3
27,7
|
|
15
|
2,0
|
2,5
|
1
2
|
1,80
1,12
|
-317,1
45,0
|
233,3
-21,2
|
198,5
-39,2
|
44,6
27,6
|
|
16
|
2,0
|
4,0
|
1
2
|
1,74
1,11
|
-201,1
92,3
|
173,9
90,6
|
145,5
-34,2
|
43,1
27,6
|
|
17
|
2,0
|
5,7
|
1
2
|
1,65
1,11
|
-163,6
6,6
|
36,4
-21,8
|
77,8
-25,2
|
40,8
27,5
|
|
18
|
2,0
|
7,0
|
1
2
|
1,57
1,10
|
-145,4
-20,4
|
-6,7
-1,9
|
46,5
-21,0
|
38,9
27,3
|
5.104. При отношении длины плитного фундамента к ширине,
более или равном двум, допускается производить совместный расчет плиты и
надфундаментных конструкций конечной жесткости, взаимодействующих с деформируемым основанием, в условиях
плоской задачи.
5.105. При расчете сооружения в продольном направлении
учитывается его реальная жесткость в этом направлении. В поперечном направлении
допускается считать сооружение абсолютно жестким. Основание работает в условиях
пространственной задачи. При расчете сооружения в поперечном направлении
основание и сооружение работают в условиях плоской деформации.
5.106. Силосный корпус и плитный фундамент,
взаимодействующие с деформируемым основанием, рассматриваются как плоская
многослойная система с жесткими или упругими связями между слоями. Связи могут
быть дискретными или континуальными. Жесткости сечений плиты и верхнего
сооружения переменные и могут меняться в широких пределах.
5.107. В качестве модели основания используется двуслойная
комбинированная модель И.Я. Штаермана - А.П. Синицына с переменным
коэффициентом жесткости верхнего винклерова слоя. Связь между плитой и
основанием двусторонняя и полная (учет касательных сил сцепления).
5.108. Нагрузка на сооружение представляется произвольной
системой вертикальных и горизонтальных сил.
5.109. В результате производимого расчета определяются
нормальные и касательные усилия на контакте плитного фундамента и
деформируемого основания, усилия в плитном фундаменте и верхнем надфундаментном
строении во всех необходимых расчетных сечениях.
5.110. В качестве основного расчетного метода используется
классический смешанный метод строительной механики в сочетании с идеями метода
Б.Н. Жемочкина определения контактных напряжений.
5.111. Сооружение разбивается на определенные горизонтальные
слои с отношением высоты слоя к его длине, позволяющим применять формулы
стержневой механики при расчете каждого слоя в отдельности. Разбивка
производится также по контакту плитного фундамента и верхнего строения и по
контакту плиты и деформируемого основания. К каждому слою прикладывается
статически определимая связь, исключающая его смещение как жесткого тела. Схема
разбивки силосного корпуса элеватора показана на рис. 52.
|
|

|
|
Рис. 52. Схема разбивки силосного корпуса
на горизонтальные слои
а - схема силосного корпуса; б - схема разбивки корпуса на слои; 1
- упругие связи между слоями, 2 - разрез
β, 3 - слой А, 4 - разрез α, 5 - слой В,
6 - разрез γ. 7 - разрез v, 8 - слой
D, 9 - разрез μ, 10 - упругое
основание
|
Линии контакта между слоями
разбиваются на определенные участки так, чтобы жесткость слоя на этом участке
была постоянной. Нормальные контактные напряжения на каждом участке
аппроксимируются линейной функцией вида
где
pi, mi
- неизвестные коэффициенты, подлежащие определению;
xi - координата центра i-го контактного участка.
Касательные контактные напряжения на
каждом участке считаются постоянными:
Схема разбивки контактной поверхности на
участки и задания неизвестных контактных напряжений показаны на рис. 53.

Рис. 53. Схема здания контактных напряжений
на горизонтальных разрезах
1 -
слой А, 2 - участки
контакта, 3 - слой В
На основе формул стержневой механики для
перемещений записываются нормальные ui и касательные vi перемещения и углы поворота φi центров контактных участков каждого слоя. Для слоя А на контактной поверхности α зависимость вектора обобщенных
перемещений от обобщенных контактных усилий на контакте α и β и
нагрузки на слой записывается в виде
|
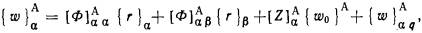
|
(233)
|
где

 - матрица перемещений от единичных сил,
вычисляемых по формуле Максвелла -Мора. Последний член в формуле (233)
описывает перемещения, определяемые смещениями слоя как жесткого тела: - матрица перемещений от единичных сил,
вычисляемых по формуле Максвелла -Мора. Последний член в формуле (233)
описывает перемещения, определяемые смещениями слоя как жесткого тела: 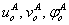 - перемещения в
направлении осей х и у и угол поворота слоя как жесткого
целого; - перемещения в
направлении осей х и у и угол поворота слоя как жесткого
целого;
 - матрица координат соответствующих точек; - матрица координат соответствующих точек;
 - вектор перемещений от внешней нагрузки. - вектор перемещений от внешней нагрузки.
Зависимость обобщенных перемещений на
контакте α слоя В записывается аналогично зависимости
(233):
|

|
(234)
|
Формулы стержневой механики, используемые
для вычисления перемещений точек контакта слоев, не учитывают вертикальные
перемещения, вызванные сжатием горизонтальных волокон слоя (местные
перемещения). Это происходит в силу принятых в сопротивлении материалов гипотез
о характере деформирования стержней. Учитывая, что местные перемещения
возникают под самой нагрузкой и имеют небольшую область распространения за ее
пределами, принято допущение, что местные перемещения пропорциональны
действующей нагрузке (аналогично модели Винклера). Механическая модель слоя в
этом случае представляет собой стержень, обладающий изгибной и сдвиговой
жесткостью и жесткостью на растяжение-сжатие, контактные поверхности которого
покрыты слоем вертикальных и горизонтальных пружин (рис. 54).
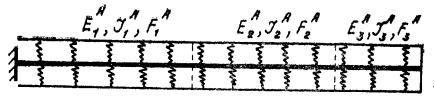
Рис. 54. Механическая модель слоя,
учитывающая местные перемещения под нагрузкой
Следовательно, при вычислении элементов
матриц  в формулы (233) и (234)
к элементам главной диагонали добавляются коэффициенты жесткости пружин
соответствующих участков. в формулы (233) и (234)
к элементам главной диагонали добавляются коэффициенты жесткости пружин
соответствующих участков.
Из условия неразрывности перемещений на
контакте а между слоями А и В с учетом наличия упругих связей между слоями с
помощью зависимостей (233) и (234) записывается система линейных алгебраических
уравнений относительно обобщенных контактных усилий и величин, определяющих
жесткие смещения слоев. К этим уравнениям добавляется система уравнений
равновесия слоя А, выражающая условие
равенства нулю реакций в связях, прикладываемых к слою для исключения его
смещения как жесткого тела. Такие системы уравнений записываются для всех
разрезов α, β, γ,...,
μ многослойной системы. В общем
виде система уравнений имеет вид:
|

|
(235)
|
где
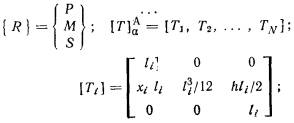
P, S и М -
суммарная нагрузка на слой в направлении оси ОУ и ОХ и
момент этой нагрузки относительно заделки;
li - длина контактного участка;
h - высота слоя;
[С]α
-диагональная матрица, элементы которой
представляют собой жесткости соответствующих упругих связей между слоями
(жесткости вертикальных колонн и диафрагм).
Система уравнений, описывающая условия
контакта нижнего слоя D (фундаментной
плиты) и упругого основания, имеет вид
|

|
(236)
|
В этом уравнении элементы матрицы 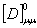 представляют собой
перемещения точек поверхности упругого основания от распределенных по
контактным участкам единичных реактивных нормальных и касательных напряжений (231) и (232); представляют собой
перемещения точек поверхности упругого основания от распределенных по
контактным участкам единичных реактивных нормальных и касательных напряжений (231) и (232);
[С]0
- диагональная матрица, элементами которой являются соответствующие
коэффициенты податливости верхнего слоя комбинированной модели основания;
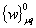 - вектор перемещений точек контакта,
вызванных нагрузкой, приложенной к основанию за пределами сооружения. - вектор перемещений точек контакта,
вызванных нагрузкой, приложенной к основанию за пределами сооружения.
5.112. После решения системы линейных алгебраических
уравнений (235), (236) с помощью выражений (231)
и (232)) получаем распределение нормальных и
касательных усилий во всех горизонтальных сечениях. Усилия в вертикальных
сечениях определяются по известным формулам стержневой механики, применяемым к
каждому слою в отдельности. Эти усилия вычисляются от действия внешней нагрузки
и определенных из предыдущего расчета напряжений в горизонтальных сечениях. По
данному алгоритму составлена программа «ПРОСТОР», предназначенная для ЭВМ типа
ЕС.
5.113. Предлагаемые алгоритм расчета плиты и программа
автоматизированных расчетов на ЭВМ разработаны на основе решения задачи об
определении напряжений на контакте плиты и линейно-деформируемого основания и
на контакте плиты и верхнего строения. Метод решения основан на идеях Б.Н.
Жемочкина об аппроксимации непрерывных функций контактных напряжений некоторым
набором локально заданных функций и удовлетворении условий контакта (равенство
перемещений плиты и поверхности основания) в дискретных точках контактной
поверхности.
5.114. При расчете плиты принимаются следующие гипотезы и
допущения:
материал плиты линейно-упругий и
однородный;
деформации плиты описываются уравнениями
технической теории тонких изгибаемых пластин;
плита конструктивно ортотропная,
переменной толщины;
контур плиты прямоугольный или ограничен
линиями, параллельными осям координат;
условия на контуре плиты произвольные.
5.115. Деформируемое основание представлено одной из
следующих линейных моделей:
однородное изотропное полупространство;
однородный изотропный слой конечной
толщины;
полупространство с переменным по глубине
модулем упругости;
комбинированная модель Репникова;
комбинированные модели, представляющие
собой последовательное соединение модели переменного коэффициента жесткости и
вышеперечисленные модели;
модель постоянного (Винклера) и
переменного коэффициента жесткости.
5.116. Верхнее надфундаментное строение считается абсолютно
жестким. Надфундаментное строение опирается на плиту посредством упругих
колонн. При расчете учитывается реальная жесткость колонн при сжатии и при
изгибе. Жесткие диафрагмы моделируются колоннами с приведенной жесткостью.
5.117. Касательные напряжения на контакте плиты и основания
не учитываются.
5.118. Для определения нормальных контактных напряжений
поверхность основания разбивается на М
прямоугольных участков линиями, параллельными декартовым осям координат.
Реактивные напряжения задаются в виде линейных степенных многочленов на каждом
контактном участке (рис. 55)

Рис. 55. Схема для определения контактных
напряжений
а -
схема сооружения; б - разбивка контактной поверхности с заданием
аппроксимирующих многочленов; 1 - упругое основание
где
δnm - символ Кронекера;
хm, ym
- координаты центра m-го участка;
pm,ij - неизвестные
коэффициенты, подлежащие определению (обобщенные реактивные напряжения).
Обобщенные перемещения поверхности
основания (v00 - нормальные перемещения, v01, v10 - углы поворота и v11 - депланация) выражаются следующей зависимостью:
|
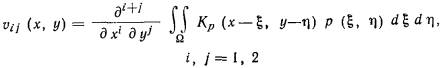
|
(238)
|
Кp(u, v) - ядро модели упругого
основания.
С учетом выражения (237) эту зависимость
можно записать в виде
|

|
(239)
|
где

После подстановки в формулу (239)
последовательно координат центров контактных участков получаем матричную
зависимость обобщенных перемещений поверхности основания от обобщенных
реактивных напряжений:
{v} = [В] {p}.
К этим перемещениям необходимо добавить
вектор обобщенных перемещений, вызванных нагрузкой, приложенной к поверхности
основания за пределами плитного фундамента (учет влияния загружения соседних
сооружений):
|
{v} = [B]
{p} + {v}q.
|
(240)
|
5.119. Расчетная схема плиты представляет собой пластину,
нагруженную произвольной поперечной нагрузкой q(x, у) и реактивным отпором основания р(х, у). Граничное
условие на каждой стороне пластины описывает один из следующих видов опирания:
свободный край, шарнирное опирание, защемление или скользящая заделка. Плита
скреплена с абсолютно жестким верхним строением посредством упругих связей. Эти
связи интерпретируются как «упругое основание с переменным коэффициентом
жесткости» (см. рис. 55). Дифференциальное уравнение изгиба такой плиты имеет
вид:
|

|
(241)
|
где
С(х, у) - переменный коэффициент жесткости «основания»,
моделирующего упругие колонны.
Для расчета собственно плиты используется
метод конечных элементов (МКЭ) с прямоугольными совместными элементами,
имеющими по четыре независимых параметра варьирования в каждом узле.
Перемещения такого элемента аппроксимируются следующей зависимостью:
|

|
(242)
|
где
Нij(х) - многочлен Эрмита.
Плита разбивается на прямоугольные
элементы в общем случае с переменным шагом так, чтобы узлы элементов совпадали
с центрами контактных участков основания. Это условие удовлетворяется для всех
внутренних узлов плиты. Несоблюдение этого условия ие вносит большой
погрешности в вычисления при достаточно большом числе конечных элементов. При
малом количестве элементов для исключения этой погрешности строится специальная
матрица перехода [F], с помощью которой можно получить перемещения пластины
не в контурных узлах, а в соседних точках, совпадающих с центрами крайних
контактных участков основания.
Система уравнений МКЭ плиты имеет вид:
где

[К] - матрица жесткости элементов;
{w} - вектор узловых обобщенных перемещений плиты (wm,00
- нормальное перемещение, wm,01, wm,10 - углы поворота и wm,11
- кручение);
{q} - вектор узловых сил, определяемых нагрузкой;
{р} - вектор обобщенных реактивных напряжений;
[Р]
- матрица коэффициентов, определяющая узловые силы от распределенных на
элементе реактивных напряжений;
[С]
-диагональная матрица, элементами которой являются жесткости соответствующих
связей.
Обобщенные
перемещения узлов пластины можно записать в виде
|
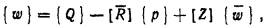
|
(244)
|
где
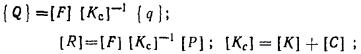
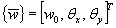 - перемещения (нормальное перемещение и два угла
поворота) плиты и верхнего строения как жесткого тела, которые необходимо
добавить к перемещениям, определяемым уравнением (243) и описывающим изгиб
плиты; - перемещения (нормальное перемещение и два угла
поворота) плиты и верхнего строения как жесткого тела, которые необходимо
добавить к перемещениям, определяемым уравнением (243) и описывающим изгиб
плиты;
[Z] - матрица координат соответствующих узлов плиты.
5.120. В качестве условия контакта принимается условие
равенства обобщенных перемещений (нормальные перемещения, два угла поворота и
кручение) узлов пластины (244) и обобщенных перемещений поверхности основания (240) соответствующих точек:
Из этого равенства с учетом формул (240) и (244) после несложных преобразований
получаем основную разрешающую систему линейных алгебраических уравнений
смешанного метода относительно неизвестных коэффициентов {р} функций, аппроксимирующих контактные напряжения, и величин 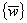 , определяющих
жесткое смещение плиты и верхнего строения: , определяющих
жесткое смещение плиты и верхнего строения:
|
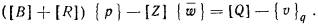
|
(246)
|
5.121. Уравнения равновесия,
которые необходимо записать для обеспечения полноты системы (246), получаются
из условия равенства нулю суммы всех вертикальных сил и суммы всех моментов,
действующих на плиту и верхнее строение:
где
Р, Мх, Му
- главные векторы сил и моментов,
действующих на верхнее надфундаментное строение.
5.122. После решения
системы уравнений (246) - (247) по формулам (240)
или (244) определяются совместные перемещения поверхности основания и плиты.
Внутренние усилия в плите определяются по известным формулам для узловых сил
метода конечных элементов. Усилия в колоннах определяются умножением
перемещений узлов пластины, полученных по формулам (244) без учета жесткого
смещения плиты, на соответствующие коэффициенты жесткости колонн:
|
{N} = [С] ({Q} - [R] {p}).
|
(248)
|
5.123. На основе этого алгоритма разработана программа
«СИРИУС» автоматизированного расчета прямоугольных плитных фундаментов,
связанных с абсолютно жестким верхним строением типа силосного корпуса
упругоподатливыми связями. Программа написана на языке ФОРТРАН-IV и реализована на ЭВМ ЕС-1022, При размещении системы
уравнений в оперативной памяти ЭВМ сетка конечных элементов может содержать до
200 узлов. Расчет производится одновременно для трех вариантов загружения.
Возможность задания переменной жесткости конечных элементов плиты и переменной
жесткости колонн позволяет моделировать различную конфигурацию плиты и
различные условия опирания верхнего строения на плитный фундамент.
5.124. Для расчета прямоугольных плитных фундаментов
постоянной толщины, связанных с абсолютно жестким верхним строением,
разработана программа «ПЛУТОН». При разработке алгоритма этой программы для
расчета собственно плиты использован метод конечных разностей (МКР). Деформации
основания описываются моделями, перечисленными выше. При аппроксимации функции
контактных напряжений в выражении (237)
сохраняется только первый член ряда. Перемещения основания записываются
аналогично формуле (240)
|
{v} = [B]
{p} + {v}q,
|
(249)
|
где
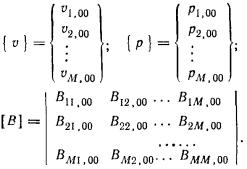
Система линейных алгебраических уравнений
МКР для плиты с учетом граничных условий и «упругого основания» имеет вид
|
([K] + [C]) {w} = {q} - {p},
|
(250)
|
где
{w} = [w1,00, w2,00, …, wM,00]T,
где
[К] - матрица коэффициентов метода конечных разностей.
Остальные обозначения описаны в формуле (243).
После решения системы уравнений (250)
получаем перемещения узлов разностной сетки плиты. С учетом смещения плиты и
верхнего строения как жесткого тела они имеют вид
|

|
(251)
|
где

Из условия равенства вертикальных
перемещений узлов разностной сетки плиты и соответствующих точек поверхности
основания получаем систему линейных алгебраических уравнений смешанного метода
относительно узловых значений контактных напряжений и смещений плиты как
жесткого тела:
|

|
(252)
|
После решения этой системы уравнений
совместно с системой (247) по формулам (251)
находят перемещения узлов сетки. Внутренние усилия в плите вычисляются по
известным формулам, усилия в колоннах - по формулам (248).
Данный алгоритм и программа «ПЛУТОН»
предназначены для расчета только прямоугольных плит постоянной жесткости. По
сравнению с программой «СИРИУС» она имеет более простой алгоритм, меньший объем
вычислительной работы и соответственно требует меньше времени работы ЭВМ при
небольшом снижении точности расчета.
Пример расчета плитного фундамента по программе
«СИРИУС»
Программа «СИРИУС» была использована при
расчете плитного фундамента и колонн подсилосного этажа корпуса готовой
продукции комбикормового завода. На рис. 56 показаны расчетные схемы
сооружения, колонн, плиты и действующие на сооружение нагрузки.

Рис. 56. Исходные данные для расчета
плитного фундамента
а - схема корпуса и действующих на
него нагрузок; б - схема плиты и
сетка колонн; в -
положительные направления моментов, действующих в сечении колонны. 1 - упругое
основание, 2 - оси симметрии
Расчет проводился при следующих
характеристиках плиты, колонн и основания:
1. Сплошная прямоугольная
железобетонная плита толщиной 0,6 м имеет размеры в плане 15 × 21 м,
изготовлена из бетона М200.
2. Железобетонные колонны
высотой 12 м, размеры сечения 0,5 × 0,5 м, изготовлены из бетона М 400.
Сетка колонн на плите имеет размеры 3 × 6 м.
3. Основание представлено
комбинированной моделью. Верхний винклеровский слой, моделирующий песчаную
подготовку, толщиной 1 м (Е1
= 20 МПа) лежит на упругом изотропном слое толщиной 20 м, модуль деформации
которого Е0 = 15 МПа, коэффициент Пуассона μ0 = 0,35.
Верхнее сооружение считается абсолютно
жестким. При расчете учитывалась реальная жесткость колонн при изгибе и сжатии.
Расчет проводился для двух случаев загружения
корпуса:
в первом варианте весь корпус загружен
хранимым продуктом, суммарная нагрузка Р = 74,7 МН;
во втором варианте - половина корпуса
загружена продуктом (одностороннее загружение). Суммарная нагрузка равна Р
= 59,6 МН. Вращающий момент, вызванный эксцентриситетом приложения нагрузки,
равен: Му = 79,6 МН·м.
В табл. 76 приведены усилия в колоннах
подсилосного этажа, а на рис. 57, 58 - эпюры нормальных реактивных напряжений,
прогибов и внутренних изгибающих моментов в плите, полученные в результате расчета
по программе «СИРИУС». Сплошной линией на рисунках показаны результаты расчета
при полном загружении, пунктирной - при одностороннем.
Таблица
76
|
Загружение
|
Усилия
|
Номера
колонн
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Полное
|
Нормальная
сила N, МН
|
4,64
|
3,12
|
2,89
|
3,12
|
4,64
|
4,91
|
3,16
|
2,80
|
3,16
|
4,91
|
|
Изгибающий
момент mx,
МН·м
|
0,050
|
0,034
|
0,013
|
0,034
|
0,050
|
0,012
|
0,012
|
0,006
|
0,012
|
0,012
|
|
Изгибающий
момент my, МН·м
|
-0,095
|
-0,041
|
0,0
|
0,041
|
0,095
|
-0,10
|
-0,03
|
0,0
|
0,03
|
0,010
|
|
Одностороннее
|
Нормальная
сила N, МН
|
2,35
|
2,08
|
2,40
|
2,91
|
5,05
|
2,43
|
2,05
|
2,23
|
2,99
|
5,41
|
|
Изгибающий
момент mх, МН·м
|
0,026
|
0,026
|
0,01
|
0,027
|
0,058
|
0,007
|
0,008
|
0,005
|
0,011
|
0,012
|
|
Изгибающий
момент my, МН·м
|
-0,026
|
0,003
|
0,012
|
0,037
|
0,136
|
-0,028
|
-0,001
|
0,013
|
0,047
|
0,132
|
Примечание. Нумерация колонн, показанных на
рис. 56 б, принята слева направо и сверху вниз.

Рис.
57. Эпюры расчетных величии
а - реактивный отпор основания, МПа, б -перемещения узлов фундамента, м.
Над
чертой - полное загружение (сплошная линия); под чертой - одностороннее
(пунктирная линия).
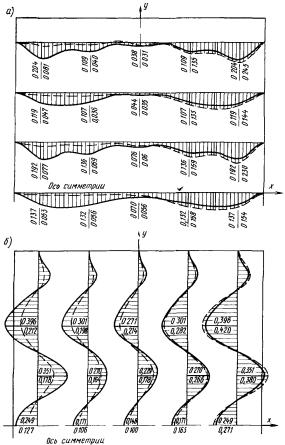
Рис. 58. Эпюры расчетных величин
а - изгибающие
моменты Мх, МН·м/м ; б - изгибающие моменты Му, МН/м.
Над чертой - полное
загружение (сплошная линия); под чертой - одностороннее (пунктирная линия).
Пример расчета силосного
корпуса по программе «ПРОСТОР»
На рис. 59 и 60 показаны результаты
расчета сооружения типа силосного корпуса, проведенного с использованием
алгоритма и программы «ПРОСТОР».

Рис. 59. Эпюры нормальных напряжений в
вертикальных и горизонтальных сечениях сооружения типа силосного корпуса,
полученные при расчете по программе «Простор» с учетом (сплошная линия) и без
учета (пунктирная) касательных контактных напряжений
N и Q - усилия в колоннах; а
- схема нагружения; б -
расчетные эпюры
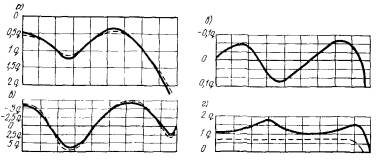
Рис. 60. Эпюры реактивных напряжений под
плитным фундаментом сооружения типа силосного корпуса и усилий в плитном
фундаменте
а - нормальных напряжений р; б - касательных напряжений τ; в - изгибающих моментов М; г - нормальных сил N
Пунктиром показаны
усилия, полученные при расчете без учета касательных контактных напряжений
Сооружение представляет собой
прямоугольную сплошную балку-стенку единичной толщины высотой 30 и длиной 36 м.
Это сооружение опирается на гибкий плитный фундамент толщиной 0,5 м посредством
упругих колонн сечением 1,0 × 1,0 м и высотой 6,0 м. Модуль упругости
материала сооружения равен 3·104 МПа. В качестве основания принята
модель упругого полупространства (Е0
= 15 МПа, μ0 = 0,35).
Сооружение нагружено по верхнему поясу равномерно распределенной нагрузкой.
Расчет проводился для двух вариантов
условий на контакте плитного фундамента и основания: с учетом и без учета
касательных реактивных напряжений.
5.125. Расчет пространственных фундаментов в форме
конической оболочки, опертой на грунт или плиту, для сооружений башенного типа
следует производить с использованием разделов руководства, касающихся расчета
оболочки при различных типах опирания и круглой или кольцевой плиты.
5.126. Указания раздела относятся к расчету фундамента в
виде осесимметричной конической оболочки переменной толщины, внутренней
поверхностью опирающейся на грунт, верхнее сечение которой - жесткий диск,
нижнее сечение свободно.
5.127. При расчете
оболочки следует принять допущения:
деформации оболочки
описываются уравнениями технической теории тонких оболочек переменной толщины с
использованием гипотез Кирхгоффа-Лява;
реакция упругого, винклеровского,
основания перпендикулярна срединной поверхности оболочки и пропорциональна
нормальной составляющей упругого перемещения основания;
материал оболочки изотропный и
линейноупругий;
силы трения между оболочкой и основанием
отсутствуют;
связи между оболочкой н основанием
нормальные к срединной поверхности, двусторонние.
5.128. Расчет оболочки должен производиться на следующие типы
нагрузок:
сосредоточенная вертикальная сила вдоль
оси оболочки;
осесимметричная нагрузка, распределенная
на поверхности конуса, меняющаяся по линейному закону вдоль образующей конуса;
краевые осесимметричные нагрузки,
учитывающиеся в краевых условиях в нижнем сечении.
5.129. Система разрешающих уравнений для конической
оболочки, опертой на винклеровское основание, имеет вид:
где
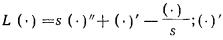
- дифференцирование по s;
s - координата, отсчитываемая от
вершины конуса (рис. 61);
α - угол между нормалью к поверхности оболочки и осью
вращения (см. рис. 61).

Рис. 61. К расчету конической оболочки на
упругом основании
а - расчетная схема фундамента; б - схема моментов и нормальных сил,
приложенных к граням элемента конической оболочки
|
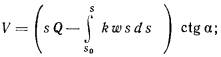
|
(254)
|
Q - поперечная сила;
kw - реакция упругого основания;
k - коэффициент жесткости основания;
w - перемещение по нормали к образующей;
 - угол поворота образующей срединной
поверхности; - угол поворота образующей срединной
поверхности;
|

|
(255)
|
|

|
(256)
|
P = P1 - P2 -
вертикальная нагрузка на оболочку, передающаяся через верхний жесткий диск;
P1 - внешняя вертикальная сила;
P2 - равнодействующая реактивной нагрузки, приложенная к
жесткому диску;
pn, pt - нормальная и касательная составляющие внешней
нагрузки на оболочку, распределенной вдоль образующей;
|
 - цилиндрическая жесткость; - цилиндрическая жесткость;
|
(257)
|
δ(s) - толщина оболочки;
Е -
модуль упругости материала оболочки;
μ - коэффициент Пуассона материала оболочки.
Следует присоединить к системе (253) уравнение w' - θ = 0
и ввести переменную
|

|
(258)
|
Система (253)
после замены переменных примет вид:
Перемещения, усилия и деформации в
оболочке должны быть выражены через переменные V = V(s), θ = θ(s), Y = Y(s) следующим
образом:
перемещение по нормали к образующей
конуса
меридиональное усилие
|

|
(261)
|
кольцевое усилие
|

|
(262)
|
меридиональный изгибающий момент
|
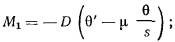
|
(263)
|
кольцевой изгибающий момент
|

|
(264)
|
поперечная сила в сечении,
перпендикулярном образующей,
|

|
(265)
|
меридиональная относительная деформация
|
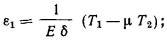
|
(266)
|
радиальная относительная деформация
|

|
(267)
|
вертикальное перемещение оболочки
|

|
(268)
|
горизонтальное перемещение оболочки
Для уравнений (268) и (269) начальными
условиями служат выражения

где
w0 = w при s = s0
Положительные направления усилий должны
приниматься в соответствии с рис. 61, а и 61, б.
Граничные условия для уравнений (259) принимаются (рис. 61,
а) по следующим формулам:
для защемленного верхнего края (s = s0):
|

|
(270)
|
для свободного от закрепления нижнего
края (s = sn):
|

|
(271)
|
5.130. Расчет
конической оболочки по расчетной схеме, приведенной на рис. 61,
а, б, следует производить с использованием разностных методов.
5.131. Требования раздела относятся к расчету осесимметричной
конической оболочки переменной толщины, верхнее сечение которой представляет
собой жесткий диск, нижнее сечение опирается на жесткое основание.
5.132. При расчете оболочки следует принимать допущения,
изложенные в п. 5.127, за
исключением допущений о реакциях основания (k = 0, Y = 0).
5.133. Расчет оболочки должен производиться на следующие
типы нагрузок:
сосредоточенная вертикальная сила вдоль
оси оболочки;
осесимметричная, распределенная по
поверхности оболочки, меняющаяся по линейному закону вдоль образующей конуса;
краевые осесимметричные нагрузки (силовые
и деформационные), различные для каждого типа опирания.
5.134. Расчет
конической оболочки следует производить с использованием системы разрешающих
уравнений:
|

|
(272)
|
где
|
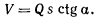
|
(273)
|
Значения D, Ф, θ, δ, Е, μ в уравнениях (272) те же, что в п. 5.130.
Усилия, деформации, вертикальные и
горизонтальные перемещения оболочки определяются по зависимостям (260) - (269),
а нормальное перемещение - по формуле
|

|
(274)
|
Положительное направление усилий должно
приниматься в соответствии с рис. 61,
б и 62, а, б, в, г.
Для конических оболочек граничные условия
на верхнем краю (s = s0) следует
принимать:
|

|
(275)
|
или через переменные V, θ:
|

|
(276)
|
5.135. Различные типы
опирания оболочки и различные виды краевой нагрузки отражаются на краевых
условиях для нижнего сечения оболочки. Эти условия при s = sn следует принять в
виде:
а) 1-й тип опирания (рис.
62, а) при заданных 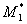 и Н*: и Н*:
|

|
(277)
|
или через переменные V и θ:
|

|
(278)
|
б) 2-й тип опирания (рис.
62, б) при заданных 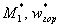 : :
|

|
(279)
|
или через переменные V и θ:
|

|
(280)
|
в) 3-й тип опирания (рис.
62,
в) при заданных : :
|
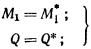
|
(281)
|
или через переменные V, θ:
|

|
(282)
|
г) 4-й тип опирания (рис.
62,
г) при заданных  : :
|

|
(283)
|
или через переменные V, θ:
|

|
(284)
|
При отсутствии усилий, перемещений и
деформаций на нижнем краю s = sn величины со
звездочкой следует положить равными нулю.
Краевую задачу для рассмотренных случаев
следует решать с использованием разностных методов.

Рис.
62. Типы опирания конической оболочки на жесткую плиту
а - подвижный шарнир; б - неподвижный шарнир; в - подвижный шарнир, реакция опоры
которого направлена вдоль образующей; г - жесткое защемление
5.136. Указания раздела
относятся к расчету осесимметрично загруженной кольцевой плиты переменной
толщины со свободными краями, лежащей на линейно-упругом, винклеровском
основании.
5.137. При расчете кольцевой плиты следует принять следующие
допущения:
деформации плиты описываются уравнениями
технической теории тонких пластин (теория Кирхгоффа);
реакция упругого основания направлена
вертикально вверх и пропорциональна упругому перемещению нижней поверхности
кольца;
материал плиты изотропный и
линейно-упругий;
силы трения между плитой и основанием
отсутствуют;
связи между плитой и основанием
вертикальные двусторонние.
5.138. Для расчета кольцевого плитного фундамента следует
использовать расчетную схему, приведенную на рис. 63, а, принимая положительные направления
внутренних усилий и перемещений в соответствии с рис. 63, а, б, в.
5.139. Дифференциальное уравнение изгиба плиты имеет
следующий вид:
где
k - коэффициент жесткости основания;
Е -
модуль упругости материала плиты;
μ - коэффициент Пуассона материала плиты;
h(r)-толщина плиты;
w(r) - вертикальное смещение срединной линии плиты;
q(r) - внешняя осесимметричная, непрерывно распределенная
нагрузка.
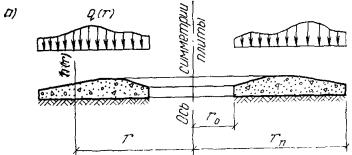

Рис.
63. К расчету кольцевой или круглой плиты конечной жесткости и системы в форме
конической оболочки, сопряженной с плитой конечной жесткости
а - схема загружения кольцевой плиты; б - направления внутренних усилий; в - то же, перемещений; г -
основная система фундамента в форме конической оболочки, сопряженной
неподвижным шарниром с плитой конечной жесткости; д - основная система фундамента в
форме конической оболочки, жестко защемленной в плите конечной жесткости
Зависимости для определения усилий в
кольцевом плитном фундаменте имеют вид:
В формулах (286) - (288) М1, М2 - изгибающие моменты в радиальном и
кольцевом направлениях соответственно;
Q - поперечная сила.
Граничные условия при r =
r0 и r = rп выражаются формулами:
|

|
(289)
|
5.140. Расчет кольцевой плиты переменной толщины следует
выполнять с использованием метода Рунге-Кутта.
Общее решение дифференциального уравнения
(285) следует представить в виде
|

|
(290)
|
где
wi - следующие частные решения для однородного уравнения
с начальными условиями: при r = r0
|

|
(291)
|
w5 - частное решение неоднородного уравнения с нулевыми
начальными условиями:
|

|
(292)
|
С1, С2, С3,
С4 - произвольные постоянные, определяемые из граничных
условий (289).
Задачи Коши нахождения частных решений w1, w2, w3, w4, w5 решаются методом Рунге-Кутта.
По краевым условиям формулы (289)
составляется система из 4 линейных уравнений для определения произвольных
постоянных.
Круглый фундамент переменной толщины
программой расчета аппроксимируется кольцевой плитой, сопряженной с жесткой
вставкой в центре.
Граничные условия выражаются формулами:
при r = r0
|

|
(293)
|
где
w0 = w при r0 (r0 - малая конечная величина, определяемая программой),
или
|

|
(294)
|
5.141. Указания раздела относятся к расчету тонкостенной
системы, состоящей из конической оболочки, опертой на кольцевую или круглую
плиту конечной жесткости, лежащую на линейно-упругом, винклеровском основании.
Расчет оболочки для первого (см. рис.
62, а) и третьего
(см. рис. 62,
в) типов опирания ничем
не отличается от аналогичного конического фундамента, опертого на жесткую
плиту, и выполняется с использованием указаний пп.
5.135, 5.136.
Плиту конечной жесткости в этом случае следует рассчитывать на действие сил,
расположенных по линии контакта.
Для шарнирно неподвижного (рис.
63, г) и защемленного (рис.
63, д) типов сопряжения
конической оболочки с плитой конечной жесткости усилия взаимодействия х1 и х2 определяются программой в результате решения системы методом
сил.
5.142. Для статического расчета упругой изотропной
осесимметрично нагруженной оболочки, лежащей на линейно-упругом, винклеровском
основании (см. рис. 61, а) принята
следующая система разрешающих уравнений в нормальной форме:
|

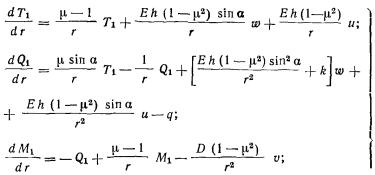
|
(295)
|
При этом усилия Т2 и М2 находятся по следующим формулам:
|
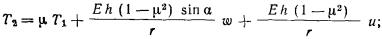
|
(296)
|
|
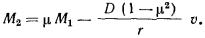
|
(297)
|
5.143. Граничные
условия для оболочки, свободно лежащей на сжимаемом основании и имеющей в
верхней части жесткую вставку, которая обеспечивает передачу осевого усилия Р от сооружения на оболочку (см. рис.
61, а), имеют вид:
при r = r0
|
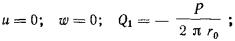
|
(298)
|
при r = rп
|

|
(299)
|
5.144. Для расчета подкрепляющего опорного кольца (кольцевой
плиты) допускается использовать уравнения (295), приняв угол конусности α = 0.
5.145. Краевую задачу о расчете конической оболочки в случае
отсутствия опорного кольца и для оболочки, сопряженной с опорным кольцом,
следует решать методом начальных параметров в сочетании с приемом деления
отрезка интегрирования на промежуточные части.
Для решения краевой задачи системы
разрешающих дифференциальных уравнений и граничные условия должны быть
представлены в векторном виде, и отрезок интегрирования разделен на ряд
промежуточных частей так, чтобы было возможно численное интегрирование
векторного разрешающего уравнения в пределах любого отрезка.
Пример расчета фундамента в форме конической оболочки,
опертой на грунт или кольцевую плиту
Параметры такой оболочки одинаковые (см. рис.
62, а): rв = 8 м, rн = 17,43
м, hф = 9,86
м, δв = δн = 0,4 м. Параметры
плиты (см. рис.
63, а): r0 = 11 м, rн = 23 м, h(r0) = h(rн)= 3 м, толщина плиты в месте сопряжения с оболочкой 5
м, коэффициент постели основания k = 50 МН/м3.
Материал: бетон М 200, Eб = 24000
МПа, Еа = 195000 МПа. Фундаменты нагружали
осесимметричной нагрузкой Р = 511000 кН. Расчеты выполнены при
отсутствии поверхностной нагрузки (Рп
= 0, Pt = 0).
Значение внутренних усилий показано на
рис. 64, а, б, где 1, 2, 3, 4 - типы закрепления оболочки на плите, 5 - соответствует оболочке, опертой
на грунт. Эпюры усилий в плите приведены на рис. 64, в, г.
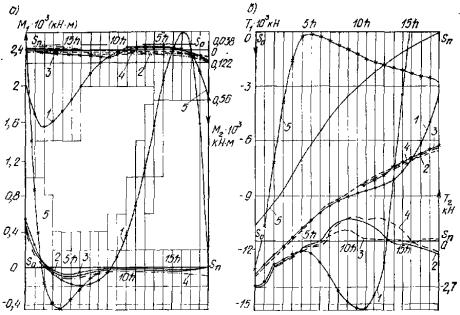


Рис. 64. К расчету конической оболочки,
опертой на грунт или кольцевую плиту конечной жесткости
а - величины меридиональных и кольцевых
моментов в оболочке; б - величины
меридиональных и кольцевых усилий в оболочке; в - величины поперечных усилий в плите; г - величины меридиональных и кольцевых моментов в плите (1, 2, 3, 4 - типы закрепления
оболочки на плите, 5 - оболочка,
опертая на грунт)
Величины напряжений растяжения и сжатия в
плите и оболочке должны быть не более расчетных характеристик бетона,
определяемых по СНиП II-21-75.
5.146. Указания раздела относятся к круглым и кольцевым
плитным фундаментам под дымовые трубы или иные отдельно стоящие, круглые в
плане сооружения башенного типа.
5.147. Изгибающие моменты в плитном фундаменте определяются
с учетом образования трещин, нелинейных деформаций железобетона и вызываемого
ими перераспределения усилий, а также с учетом жесткости надфундаментного
строения. Расчетная схема фундамента приведена на рис. 65.

Рис. 65. Расчетная схема и результаты
расчета
1 - плитный фундамент; 2 - стакан фундамента; 3 - подфундаментное строение
Действующая на плитный
фундамент нагрузка приводится к погонной осесимметричной нагрузке Р (см. рис. 65), определяемой по
формуле
|

|
(300)
|
где
N -
равнодействующая вертикальной нагрузки на плитный фундамент от веса сооружения
вместе со стаканом фундамента;
Мв - результирующий момент внешних сил относительно
подошвы плитного фундамента;
rp - радиус приложения нагрузки Р.
Неизвестные усилия в местах сопряжений
стакана фундамента с плитой и надфундаментным строением (см. рис. 65) находятся
из условий совместности деформаций. При этом стакан фундамента и надфундаментное
строение допускается считать линейно-упругими. Для основания принимается
расчетная схема по указаниям разд. 1 в виде линейно-деформируемого слоя,
либо основания, подчиняющегося гипотезе переменного коэффициента жесткости, либо как комбинация этих схем.
Расчет плитного фундамента производится
на ЭВМ вариационно-разностным методом путем последовательных приближений. В
каждом приближении производится расчет анизотропного линейно-упругого плитного
фундамента, жесткости которого определяются по результатам предыдущего
приближения в соответствии с указаниями пп. 5.148. и 5.149.
В первом приближении плитный фундамент предполагается изотропным, а его
жесткости вычисляются по формуле (304). Процесс последовательных приближений
заканчивается, когда разница в кривизнах для двух соседних приближений будет
составлять не более 2 %.
Для обеспечения необходимой точности
расчета плитный фундамент следует разбивать разностными узлами не менее чем на
20 участков по радиусу.
5.148. Элемент плиты может находиться в
одной из четырех стадий работы: линейно-упругой; упругопластической без трещин;
упругопластической с трещинами; предельной.
Уравнения, устанавливающие связь между
изгибающими моментами и кривизнами, для всех стадий записываются в виде:
где
Мr и Мφ - радиальный и окружной изгибающие моменты;
Dr, Dr φ. Dφ - жесткости;
Кr, Кφ
- радиальная и окружная кривизны,
определяемые по формулам:
|

|
(302)
|
в которой w - функция прогибов; r - текущий радиус.
1-я
стадия ограничивается неравенствами:
|

|
(303)
|
где
Мт - изгибающий момент трещинообразования, определяемый
по формуле

где
h - толщина элемента плиты;
Rp11 -
расчетное сопротивление бетона осевому растяжению для предельного состояния
второй группы.
В 1-й стадии жесткости вычисляются
следующим образом:
|

|
(304)
|
где
0,2 - коэффициент поперечной деформаций
бетона;
Еб - начальный модуль упругости бетона;
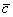 - коэффициент, учитывающий влияние длительной
ползучести бетона, определяемый по формуле - коэффициент, учитывающий влияние длительной
ползучести бетона, определяемый по формуле
|

|
(305)
|
сн - коэффициент, принимаемый равным 2 при влажности
окружающей среды выше 40 % и равным 3 при влажности окружающей среды 40 % и
ниже;
αд -
коэффициент длительности действия нагрузки, определяемый по формуле
|
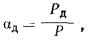
|
(306)
|
где
Рд - часть
полной нагрузки Р, включающая
в себя постоянные и длительные нагрузки.
2-я стадия наступает, когда оба изгибающих момента по абсолютной
величине не превышают Мт,
но хотя бы один из них превосходит 0,5 Мт.
Жесткости при этом определяются следующим образом:
Жесткость Dφ определяется аналогично заменой индекса r на φ, а
Drφ вычисляется по формуле
|
Drφ = 0,1(Dr + Dφ).
|
(308)
|
3-я стадия достигается, когда один из моментов Мr или Мφ
превысит момент трещинообразования. Предполагается, что по площадке действия
этого момента появляется трещина. При дальнейшем увеличении нагрузки второй
момент также может достичь трещинообразования и появятся трещины второго
направления. Жесткости для третьей стадии работы элемента плиты определяются по
формулам:
Жесткость Dφ определяется
аналогично, заменой индекса r на φ, а Drφ = 0.
В этих формулах:
h0 - полезная высота сечения;
μ - коэффициент армирования;
Еа - модуль
упругости арматуры;
n = Еа/Еб;
ξ
- относительная высота сжатой зоны бетона в сечении с трещиной;
ψа -
коэффициент, учитывающий работу растянутого бетона на участке с трещинами;
ψб -
коэффициент, учитывающий неравномерность деформаций сжатой грани сечения и
принимаемый равным 0,9;
 - коэффициент, учитывающий снижение модуля
деформации бетона сжатой зоны. - коэффициент, учитывающий снижение модуля
деформации бетона сжатой зоны.
Параметры ξr(φ) и ψаr(φ)
являются функциями соответствующих изгибающих моментов Мr или Мφ.
Относительная высота сжатой зоны определяется по формуле
|

|
(311)
|
где
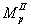 - предельный изгибающий момент, который может воспринять сечение,
определяемый по формуле - предельный изгибающий момент, который может воспринять сечение,
определяемый по формуле
RaII и RпpII - расчетные сопротивления
арматуры растяжению и бетона осевому сжатию для предельных состояний второй
группы
|
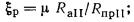
|
(313)
|
|
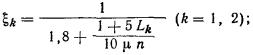
|
(314)
|
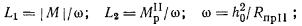
с = 3, если ξp ≥ ξ2;
с = 5, если ξp < ξ2.
Коэффициент ψа вычисляется по формуле
|

|
(315)
|
но принимается не более 1.
Здесь  - коэффициент, учитывающий
длительность действия нагрузки и определяемый по формуле - коэффициент, учитывающий
длительность действия нагрузки и определяемый по формуле
|
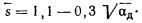
|
(316)
|
Коэффициент  определяется по
формуле определяется по
формуле
|

|
(317)
|
где
vд - коэффициент, принимаемый равным 0,15 при влажности
окружающей среды выше 40 % и равным 0,1 при влажности окружающей среды 40 % и
ниже.
4-я
стадия работы элемента плиты
наступает, когда одна из кривизн Кr или Кφ достигает своего критического значения  или или  , определяемого по формулам для третьей стадии при значениях
соответствующих изгибающих моментов, равных , определяемого по формулам для третьей стадии при значениях
соответствующих изгибающих моментов, равных 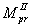 , или , или  . .
Предполагается, что при  образуется кольцевая
(радиальная) линия излома. В сечении, совпадающем с линией излома, напряжения в
арматуре достигают RaII, напряжения в бетоне сжатой зоны RпрII, а увеличение кривизны в направлении,
перпендикулярном линии излома, происходит при постоянном значении
соответствующего изгибающего момента, равного предельному (рис. 66). образуется кольцевая
(радиальная) линия излома. В сечении, совпадающем с линией излома, напряжения в
арматуре достигают RaII, напряжения в бетоне сжатой зоны RпрII, а увеличение кривизны в направлении,
перпендикулярном линии излома, происходит при постоянном значении
соответствующего изгибающего момента, равного предельному (рис. 66).

Рис. 66. Диаграмма деформирования
железобетона
Жесткости в этой стадии определяются по
формулам:
|

|
(318)
|
Если одна из кривизн меньше своего
критического значения, то соответствующая жесткость вычисляется по формулам (309) - (310).
5.149. При расчете
плитного фундамента жесткости для (k + 1) приближения определяются по кривизнам
предыдущего приближения k.
Для этого вначале определяются
характерные кривизны диаграммы деформирования для каждого узла разностной сетки
в радиальном и окружном направлениях:
 - максимальная кривизна в направлении r (или φ),
когда имеются только радиальные (или только кольцевые) трещины; - максимальная кривизна в направлении r (или φ),
когда имеются только радиальные (или только кольцевые) трещины;
 - кривизна в направлении r (φ),
соответствующая началу упрочнения на диаграмме деформирования; - кривизна в направлении r (φ),
соответствующая началу упрочнения на диаграмме деформирования;
 - кривизна, соответствующая образованию линий
излома. - кривизна, соответствующая образованию линий
излома.
Характерные кривизны вычисляются по
формулам:
где
 - вычисляется по формуле (309) при Мr(φ) = Мт; - вычисляется по формуле (309) при Мr(φ) = Мт;
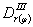 - вычисляется по формуле (309) при - вычисляется по формуле (309) при  . .
При вычислении характерных кривизн
следует учитывать, что их величины будут зависеть от того, какие волокна
растягиваются - верхние или нижние. В соответствии с этим в расчет надо вводить
либо верхнюю, либо нижнюю арматуру.
При вычислении жесткостей стадия работы
элемента плитного фундамента определяется по его кривизнам. Если выполняется
хоть одно из условий
|

|
(322)
|
где
 - кривизны k-го приближения, то при определении жесткостей (k + 1)-го
приближения предполагается, что элемент работает с трещинами. В этом случае - кривизны k-го приближения, то при определении жесткостей (k + 1)-го
приближения предполагается, что элемент работает с трещинами. В этом случае  , а диаграмма деформирования имеет вид, изображенный на рис.
66. Жесткости для (k + 1)-го
приближения , а диаграмма деформирования имеет вид, изображенный на рис.
66. Жесткости для (k + 1)-го
приближения  и и 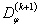 вычисляются по
формуле вычисляются по
формуле
|

|
(323)
|
Изгибающий момент Mr(φ) в формуле (323) определяется следующим образом.
Если

Если  то то 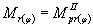 и образуется
кольцевая (радиальная) линия излома. и образуется
кольцевая (радиальная) линия излома.
На участках 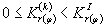 и и  (см. рис. 66) Mr(φ) может быть определен методом хорд с использованием
соответственно формулы (310) и формулы (309) для описания диаграммы деформирования. (см. рис. 66) Mr(φ) может быть определен методом хорд с использованием
соответственно формулы (310) и формулы (309) для описания диаграммы деформирования.
Если не выполняется ни одно из условий
(322), то жесткости для (k + 1)-го приближения вычисляются но формулам:
|

|
(324)
|
|

|
(325)
|
где
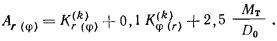
При выводе этих формул использовалась
система уравнений (301) и предполагалось,
что для жесткостей Dr и Dφ справедлива формула (307).
Если значения  или или 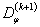 по формуле (324)
получаются больше, чем D0, то их
следует принять равными D0. Если по формуле (324)
получаются больше, чем D0, то их
следует принять равными D0. Если  или или  получаются меньше,
чем 0,8 D0, то это
означает, что элемент плиты работает с трещинами. В этом случае следует принять получаются меньше,
чем 0,8 D0, то это
означает, что элемент плиты работает с трещинами. В этом случае следует принять
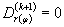 , а жесткости , а жесткости  и и 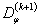 вычислять по формуле
(323). вычислять по формуле
(323).
5.150.
Рабочая арматура плитного фундамента
должна обеспечивать его прочность и допустимую ширину раскрытия трещин. Кроме
того, количество арматуры в сечениях с трещинами должно обеспечивать выполнение
условия
где
Мр - предельный изгибающий момент в сечении при расчете
на прочность, определяемый по формуле (312)
при характеристиках бетона и арматуры для предельных состояний первой группы.
Следует учитывать, что усилия в плитном
фундаменте при определении их с учетом нелинейных деформаций железобетона
существенно зависят от принятого армирования. Поэтому подбор арматуры следует
выполнять методом последовательных приближений. Предварительные размеры
участков армирования и количество арматуры в сечениях могут назначаться из
линейного расчета с последующим корректированием их по усилиям нелинейного
расчета.
Допускается не ставить рабочей арматуры в
сечениях, где не образуется трещин при расчете по прочности, т.е. выполняется
условие
|

|
(327)
|
где
 - изгибающий момент в сечении от действия нагрузки Р с коэффициентом перегрузки больше
единицы; - изгибающий момент в сечении от действия нагрузки Р с коэффициентом перегрузки больше
единицы;
0,9 - коэффициент условий работы;
Rp - расчетное сопротивление бетона осевому растяжению
для предельных состояний первой группы,
5.151. Расчет плитного
фундамента по прочности должен выполняться на действие нагрузки Р с коэффициентом перегрузки больше
единицы. Если радиальный (окружной) изгибающий момент превосходит
соответствующее значение Мр, то предполагается образование кольцевой (радиальной) линии
излома. Следует считать, что прочность фундамента обеспечена, если радиальные и
кольцевые линии излома не образуют областей, делящих его на отдельные части.
5.152. Плитный фундамент
должен рассчитываться на раскрытие вертикальных трещин в радиальных и окружных
сечениях при выполнении условия
где
М -
изгибающий момент в сечении от действия нагрузки Р с коэффициентом перегрузки равным
единице.
Ширину кратковременного раскрытия трещин ат.кр следует вычислять по
формуле
|

|
(329)
|
Ширину длительного раскрытия трещин ат.дл следует вычислять по
формуле
|

|
(330)
|
В формулах (329) и (330):
ат1 -
ширина раскрытия трещин от кратковременного действия нагрузки Р;
kн, kд -
коэффициенты, учитывающие работу растянутого бетона над трещинами в
слабоармированных сечениях (μ
≤ 0,008);
сд -
коэффициент, принимаемый равным 1,5 для фундаментов, эксплуатируемых выше
уровня грунтовых вод, и равным 1,2 для фундаментов, эксплуатируемых ниже уровня
грунтовых вод. Ширина раскрытия трещин от кратковременного действия нагрузки Р, мм, должна определяться по формуле
|

|
(331)
|
где
σа -
напряжение в растянутой арматуре, вычисляемое по формуле
|
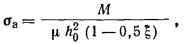
|
(332)
|
в которой ξ вычисляется согласно
указаниям п. 5.148;
Еа - модуль
упругости арматуры;
d - диаметр растянутой арматуры, мм.
Коэффициент Кн, учитывающий уровень нагружения, вычисляется по
формуле
|
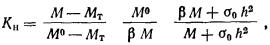
|
(333)
|
где М0 -
изгибающий момент, при котором растянутый бетон над трещинами практически
выключается из работы, равный:
|
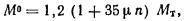
|
(334)
|
но не более 3,3 Мт;
β - коэффициент, принимаемый равным 1 при вычислении σт.кр и равным ад при вычислении ат.дл; σ0 = 0,17 МПа.
Коэффициент kд,, учитывающий длительность действия нагрузки,
определяется по формуле
|
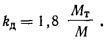
|
(335)
|
Коэффициенты kн и kд принимаются равными единице, если не выполняется хоть
одно из условий:
μ ≤ 0,008;
M < M0
kн kд < 1
5.153. По описанному алгоритму разработана программа АРПОС-2
для ЕС ЭВМ. Программа позволяет делать поверочный расчет либо подбирать
армирование из условий прочности плитного фундамента и допустимой ширины
раскрытия трещин. В качестве моделей основания используются упругий слой,
модель с переменным по радиусу коэффициентом жесткости и комбинация этих двух
моделей. Программа написана на ФОРТРАНе и требует ЭВМ с объемом внутренней
памяти не менее 128 К.
Пример
Подобрать армирование для плитного
фундамента, изображенного на рис. 65. N = 200 MH; Мв = 500 МН·м; коэффициенты
перегрузки kN = 1,1; kм = 1,3.
Основание - слой толщиной 14 м с модулем упругости E = 30 МПа (с учетом коэффициента условий работы
основания mr = 1,5). Бетон М 300; арматура A-III диаметром 28
мм. Фундамент находится ниже уровня грунтовых вод. Предельная ширина раскрытия
трещин: длительная - 0,2 мм, кратковременная - 0,3 мм. Результаты расчета
приведены на рис. 65.
5.154. Предлагаемая методика используется для решения
статических задач по расчету круглых плитных фундаментов, лежащих на
линейно-деформируемом основания с переменными по глубине упругими
характеристиками (модулем деформации Е и коэффициентом Пуассона v).
5.155. Расчет плит может производиться как на основе теории
тонких изгибаемых пластин (теории Кирхгоффа), так и на основе теории пластин
средней толщины (теории Рейсснера).
Толщина плитного фундамента h считается постоянной, материал - изотропным.
Допустимыми для расчета нагрузками могут
быть только нагрузки, симметричные относительно центра:
вертикальная равномерно распределенная
нагрузка по кругу (в том числе и по всей плите) или по кольцу;
вертикальная равномерная силовая нагрузка
по окружности (в том числе и по краю плиты);
равномерная моментная нагрузка по
окружности (в том числе и по краю плиты);
сосредоточенная сила в центре плиты;
горизонтальные растягивающие (сжимающие)
усилия, приложенные по краю плиты.
Трение между плитой и основанием не
учитывается.
Связи между плитой и основанием
вертикальные, двусторонние.
5.156. На основе сделанных предпосылок (пп. 5.154, 5.155)
задача о расчете круглых плитных фундаментов на линейно-деформируемом основании
математически может быть сформулирована в виде следующих уравнений, записанных
в полярной системе координат:
где
w(r) -прогиб плиты;
R - радиус плиты;
р(r) -заданная внешняя нагрузка;
q(r) - контактное давление на плиту со стороны основания;
A - дифференциальный оператор изгиба плиты.
Для тонких плит при вертикальной нагрузке

где
D = Eh3[12 (1 - v2)]-1
- цилиндрическая жесткость плиты на изгиб;
v - коэффициент Пуассона.
Для тонких плит при одновременном
действии вертикальных и горизонтальных усилий
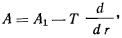
где
Т -
горизонтальные усилия, распределенные по краю срединной плоскости плиты.
Для плит средней толщины, рассчитываемых
по теории Рейсснера,

Г1, Г2 - граничные условия для плиты. Чаще всего это условия
свободного края. В интегральном уравнении (339) θ имеет размерность напряжения и характеризует упругие
свойства основания. Н имеет
размерность длины и является основной геометрической характеристикой основания.
К(х) -
эллиптический интеграл первого рода. Функция F(t, τ) имеет вид

где L(u) - функция, определяемая выбранной моделью
линейно-деформируемого основания.
Для однородного упругого полупространства
L(u) = 1.
В случае модели линейно-деформируемого
основания с произвольно изменяющимися по глубине упругими характеристиками
функция L(u) задается численно, если аналитическое ее представление
невозможно.
Метод решения поставленной задачи основан
на использовании специальных ортонормированных полиномов, позволяющих сопрягать
решения дифференциального уравнения относительно прогиба плиты (336) и интегрального уравнения для расчета отпора упругого
основания (339).
Решение проводится в три этапа.
На первом этапе строится специальная
система полиномов Qk(r), удовлетворяющих граничным
условиям (337), (338) и ортонормированных по отношению к дифференциальному
оператору A, описывающему деформацию плиты, т. е. полученная
ортогональная система полиномов Qk(r) удовлетворяет следующему условию:
|

|
(340)
|

δkm - символ Кронеккера.
Функция прогиба представляется в виде
ряда по полиномам Qk(r)
|

|
(341)
|
На втором этапе строится решение
интегрального уравнения (339).
При этом, учитывая линейность задачи,
контактное давление может быть представлено в виде линейной комбинации частных
решений с теми же коэффициентами, что и функция прогиба:
|

|
(342)
|
После подстановки рядов (341) и (342) в
интегральное уравнение (339) и приведения последнего к безразмерному виду
получим k интегральных
уравнений для определения qh(f):
|

k = 1, 2, …
|
(343)
|
где безразмерный параметр s = θ R3 D-1
характеризует жесткость плиты и основания, λ = HR-1. Для решения интегральных уравнений (343) использован
метод сведения каждого из них к бесконечной алгебраической системе уравнений с
помощью разложения функций qk(r), Qk(r),
F(t, τ) в ряды по собственным функциям главной части
интегрального оператора.
На третьем этапе происходит сопряжение
решений для прогиба плиты (341) с решением соответствующей контактной задачи
(342). При этом ряды (341) и (342) подставляем в дифференциальное уравнение
изгиба плиты (336)
и с учетом условия ортогональности (340) и условия статики приходим к
бесконечной линейной алгебраической системе уравнений для определения
коэффициентов dk.
Зная bk, можно по формуле (341) найти прогибы плиты и другие
характеристики рассматриваемой задачи.
Изложенный алгоритм реализован в виде
вычислительной программы на языке ФОРТРАН для ЭВМ типа ЕС-1022.
Программа позволяет определять
напряженно-деформированное состояние плиты в широком диапазоне изменения
параметров λ, s при различных моделях основания и видах нагружения.
Пример. В качестве модели основания рассматривается слой,
свободно лежащий на упругом полупространстве:

χ = θ1/θ2, где θ1, θ2 характеризуют
механические свойства слоя и полупространства;
θi = Gi/(1-vi), Gi vi(i =1, 2) - соответственно модуль сдвига и коэффициент
Пуассона материала слоя и полупространства.
Анализ результатов расчета показывает,
что в центральной зоне плиты отпор основания значительно уменьшается с
увеличением параметра χ (χ > 1) и уменьшением
относительной толщины верхнего слоя. При некоторых соотношениях параметров λ, χ, s отпор
основания становится отрицательным как при равномерно распределенной, так и при
сосредоточенной нагрузке.
Так, например, для s = l, χ =
5, λ = 1 отпор
основания и изгибающий момент при равномерно распределенной нагрузке р(r) = 1 в центре плиты имеют значения: q(r) =0,101, Mr = 0,139.
Результаты приведены в безразмерном виде.
Размерные величины нагрузки р*(r'), отпора
q*(r'), момента  можно получить по формулам: можно получить по формулам:

6. КОНСТРУКТИВНЫЕ
ТРЕБОВАНИЯ
6.1. Конструирование плитных фундаментов выполняют в
соответствии с указаниями главы СНиП по проектированию бетонных и
железобетонных конструкций, «Руководства по конструированию бетонных и
железобетонных конструкций из тяжелого бетона (без предварительного
напряжения)», а также с учетом дополнительных требований настоящего раздела.
6.2. При проектировании фундаментов принимают, как
правило, бетон марки М 200 и при соответствующем обосновании - бетон марки М
300. Рабочую арматуру принимают периодического профиля класса A-III, в случае
необходимости ограничения раскрытия трещин - периодическую класса А-II. Монтажную, распределительную, а также конструктивную
арматуру принимают гладкую класса A-I.
Как правило, для армирования следует
применять унифицированные арматурные изделия; отдельные стержни рекомендуется
применять только в качестве дополнительного армирования или при невозможности
или нерациональности применения сварных сеток.
6.3. Сечения железобетонных плитных фундаментов следует
назначать из расчета по действующим усилиям и соответствующим группам
предельных состояний с учетом экономических требований, необходимости
унификации опалубки, арматурных изделий и принятой технологии производства
работ.
Принятые сечения должны обеспечивать
правильность расположения арматуры в сечении, защитные слои и анкеровку
арматуры.
Способ армирования следует выбирать на
основе технико-экономического сравнения в зависимости от величины и характера
распределения усилий в плитном фундаменте, его размеров, способа
транспортирования и монтажа арматурных изделий и условий производства работ.
Возможны следующие способы армирования:
унифицированными сварными сетками;
унифицированными сварными сетками с
дополнительным армированием отдельными стержнями;
вязаной арматурой.
6.4. При армировании плитных фундаментов унифицированными
сетками и отдельными стержнями несущую способность сечений на изгиб М и соответствующие проценты
армирования μ допускается
определять по табл. 77-80 в зависимости от марки бетона, толщины плитного
фундамента, диаметров dс, площади арматуры Fa и шагов стержней рабочей
арматуры. Таблицы составлены в соответствии с положениями главы СНиП по
проектированию бетонных и железобетонных конструкций. Несущая способность
сечений определена как для изгибаемых элементов прямоугольного сечения шириной
1 м в предположении одиночного армирования.
Таблица 77
|
Схемы армирования
|
При толщине плитных фундаментов из бетона марки М
200, мм
|
|
400
|
500
|
600
|
700
|
800
|
900
|
1000
|
1100
|
1200
|
1300
|
1400
|
1500
|
1600
|
1700
|
1800
|
1900
|
2000
|
|

|
dс =25 мм
Fа = 24,5 см2
|
0,69
21,9
|
0,54
28,8
|
0,44
35,8
|
0,37
42,8
|
0,32
49,8
|
0,28
56,8
|
0,25
63,7
|
0,23
70,7
|
0,21
77,7
|
0,19
84,7
|
0,18
91,7
|
0,16
98,7
|
0,15
105,6
|
0,14
112,6
|
0,13
119,6
|
0,13
126,6
|
0,12
133,6
|
|
dc =
32 мм
Fа = 40,2 см2
|
1,15
32,6
|
0,89
44,1
|
0,73
55,6
|
0,61
67,0
|
0,53
78,5
|
0,47
89,9
|
0,42
101,4
|
0,38
112,8
|
0,34
124,3
|
0,32
135,8
|
0,29
147,2
|
0,27
158,7
|
0,25
170,1
|
0,24
181,6
|
0,22
193,0
|
0,21
204,5
|
0,20
216,0
|
|

|
dc
=25 мм
Fa =
49,l см2
|
1,46
36,1
|
1,12
50,1
|
0,91
64,1
|
0,77
78,1
|
0,66
92,1
|
0,58
106,1
|
0,52
120,1
|
0,47
134,0
|
0,43
148,0
|
0,39
162,0
|
0,36
176,0
|
0,34
190,0
|
0,31
204,0
|
0,30
218,0
|
0,28
232,0
|
0,26
246,0
|
0,25
260,0
|
|
dc = 32 мм
Fa
=80,4 см2
|
-
-
|
1,87
69,1
|
1,51
92,0
|
1,27
114,9
|
1,10
137,8
|
0,96
160,7
|
0,86
183,7
|
0,78
206,6
|
0,71
229,5
|
0,65
252,4
|
0,60
275,3
|
0,56
298,2
|
0,52
321,1
|
0,49
344,0
|
0,46
367,0
|
0,43
389,0
|
0,41
412,8
|
|

|
dc =
25 мм
Fa
=49,1 см2
|
1,39
38,4
|
1,08
52,4
|
0,88
66,4
|
0,75
80,4
|
0,65
94,4
|
0,57
108,4
|
0,51
122,4
|
0,46
136,4
|
0,42
150,3
|
0,39
164,3
|
0,36
178,3
|
0,33
192,3
|
0,31
206,3
|
0,29
220,3
|
0,28
234,3
|
0,26
248,3
|
0,25
262,3
|
|
dc
=32 мм
Fa
=80,4 см2
|
-
-
|
1,79
73,7
|
1,46
96,6
|
1,23
119,5
|
1,07
142,4
|
0,94
165,3
|
0,84
188,2
|
0,76
211,1
|
0,69
234,1
|
0,64
257,0
|
0,59
279,9
|
0,55
302,8
|
0,51
325,7
|
0,48
348,6
|
0,45
371,5
|
0,43
394,5
|
0,41
417,4
|
Продолжение табл. 77
|

|
dс = 25 мм
Fa =
87,3 см2
|
-
-
|
-
-
|
1,65
96,5
|
1,39
121,4
|
1,20
146,3
|
1,05
171,1
|
0,94
196,0
|
0,85
220,9
|
0,77
245,8
|
0,71
270,7
|
0,65
295,5
|
0,61
320,4
|
0,57
345,3
|
0,53
370,2
|
0,50
395,1
|
0,47
419,9
|
0,45
444,8
|
|
dc =
32 мм
Fa
=103 см2
|
-
-
|
-
-
|
1,96
106,1
|
1,64
135,4
|
1,42
164,8
|
1,24
194,1
|
1,11
223,5
|
1,00
252,9
|
0,91
282,2
|
0,84
311,6
|
0,77
340,9
|
0,72
370,3
|
0,67
399,6
|
0,63
429,0
|
0,59
458,3
|
0,56
487,7
|
0,53
517,0
|
|
|
dc =
25 мм
Fa = 87,3 см2
|
-
-
|
1,95
76,8
|
1,59
101,7
|
1,34
126,6
|
1,16
151,4
|
1,03
176,3
|
0,92
201,2
|
0,83
226,1
|
0,76
251,0
|
0,70
275,8
|
0,64
300,7
|
0,60
325,6
|
0,56
350,5
|
0,53
375,4
|
0,49
400,2
|
0,47
425,1
|
0,44
450,0
|
|
dc
=32 мм
Fa =
103,0 см2
|
-
-
|
-
-
|
1,88
112,5
|
1,59
141,9
|
1,37
171,2
|
1,21
200,6
|
1,08
229,9
|
0,95
259,3
|
0,89
288,6
|
0,82
318,0
|
0,76
347,4
|
0,71
376,7
|
0,66
406,1
|
0,62
435,4
|
0,58
464,8
|
0,55
494,1
|
0,52
523,5
|
|
|
dc =
200 мм
Fa =
75,4 см2
|
1,82
43,9
|
1,41
61,8
|
1,15
79,7
|
0,97
97,6
|
0,84
115,5
|
0,74
133,4
|
0,66
151,3
|
0,60
169,2
|
0,54
187,1
|
0,50
205,0
|
0,46
222,9
|
0,43
240,8
|
0,40
258,7
|
0,38
276,6
|
0,35
294,5
|
0,34
312,4
|
0,32
330,3
|
|
dc =150 мм
Fa = 83,8 см2
|
-
-
|
1,88
74,5
|
1,53
98,4
|
1,29
122,3
|
1,12
146,2
|
0,99
170,1
|
0,88
194,0
|
0,80
217,8
|
0,73
241,7
|
0,67
265,6
|
0,62
289,5
|
0,57
313,4
|
0,54
337,3
|
0,50
361,1
|
0,48
385,0
|
0,45
408,0
|
0,43
432,8
|
|
d =100 мм
|
-
|
-
|
-
|
1,94
|
1,68
|
1,48
|
1,33
|
1,20
|
1,09
|
1,00
|
0,93
|
0,86
|
0,81
|
0,76
|
0,72
|
0,68
|
0,64
|
Продолжение табл. 77
|
Схемы армирования
|
При толщине плитных фундаментов из бетона марки М
200, мм
|
|
400
|
500
|
600
|
700
|
800
|
900
|
1000
|
1100
|
1200
|
1300
|
1400
|
1500
|
1600
|
1700
|
1800
|
1900
|
2000
|
|
|
Fa =
l25,7 см2
|
-
|
-
|
-
|
159,7
|
195,5
|
231,4
|
267,2
|
303,0
|
338,8
|
374,7
|
410,5
|
446,3
|
482,1
|
518,0
|
553,8
|
589,6
|
625,4
|
|
dc =
200 мм
Fa =
125,7 см2
|
-
-
|
-
-
|
-
-
|
-
-
|
1,74
186,9
|
1,53
222,8
|
1,36
258,6
|
1,23
294,4
|
1,12
330,2
|
1,02
366,1
|
0,95
401,9
|
0,88
437,7
|
0,82
473,5
|
0,77
509,4
|
0,73
545,2
|
0,69
581,0
|
0,65
616,8
|
|
dc =
l50 мм
Fa =
167,6 см2
|
-
-
|
-
-
|
-
-
|
-
-
|
-
-
|
-
-
|
1,81
313,1
|
1,64
360,9
|
1,49
408,7
|
1,37
456,4
|
1,26
504,2
|
1,17
551,9
|
1,10
599,7
|
1,03
647,5
|
0,97
695,2
|
0,92
743,0
|
0,87
790,8
|
Примечание. Над чертой дано армирование μ, %; под чертой -
соответствующая несущая способность на изгиб М, кН·м·10, плитных фундаментов, армированных арматурой класса А-III.
Таблица 78
|
Схемы армирования
|
При толщине плитных фундаментов из бетона марки М
200, мм
|
|
400
|
500
|
600
|
700
|
800
|
900
|
1000
|
1100
|
1200
|
1300
|
1400
|
1500
|
1600
|
1700
|
1800
|
1900
|
2000
|
|

|
dс = 25 мм
Fa = 24,5 см2
|
0,69
27,6
|
0,54
36,8
|
0,44
46,0
|
0,37
55,2
|
0,32
44,4
|
0,28
73,6
|
0,25
82,8
|
0,23
92,0
|
0,21
101,1
|
0,19
110,3
|
0,18
119,5
|
0,16
128,7
|
0,15
137,9
|
0,14
147,1
|
0,13
156,3
|
0,13
165,5
|
0,12
174,6
|
|
dc =
32 мм
Fa = 40,2 см2
|
1,15
39,9
|
0,89
55,0
|
0,73
70,1
|
0,61
85,2
|
0,53
100,2
|
0,47
115,3
|
0,42
130,4
|
0,38
145,5
|
0,34
160,5
|
0,32
175,6
|
0,29
190,7
|
0,27
205,8
|
0,25
220,8
|
0,24
235,9
|
0,22
251,0
|
0,21
266,1
|
0,20
281,1
|
|

|
dс = 25 мм
Fa = 49,1 см2
|
-
|
1,12
61,4
|
0,91
79,8
|
0,77
98,2
|
0,66
116,6
|
0,58
135,0
|
0,52
153,5
|
0,47
171,9
|
0,43
190,3
|
0,39
208,7
|
0,36
227,1
|
0,34
245,5
|
0,31
263,9
|
0,30
282,3
|
0,28
300,8
|
0,26
319,2
|
0,25
337,6
|
|
dc =
32 мм
Fa = 80,4 см2
|
-
|
-
|
-
|
1,27
139,1
|
1,10
169,2
|
0,96
199,4
|
0,86
229,5
|
0,78
259,7
|
0,71
289,8
|
0,65
320,0
|
0,60
350,1
|
0,56
380,3
|
0,52
410,4
|
0,49
440,6
|
0,46
470,7
|
0,43
500,9
|
0,41
531,0
|
|

|
dc =
25 мм
Fa =
49,1 см2
|
1,39
46,0
|
1,08
64,4
|
0,88
82,8
|
0,75
101,3
|
0,65
119,7
|
0,57
138,1
|
0,51
156,5
|
0,46
174,9
|
0,42
193,3
|
0,39
211,7
|
0,36
230,1
|
0,33
248,6
|
0,31
267,0
|
0,29
285,4
|
0,28
303,8
|
0,26
322,2
|
0,25
340,6
|
|
dc =
32 мм
Fa = 80,4 см2
|
-
|
-
|
-
|
1,23
145,1
|
1,07
175,3
|
0,94
205,4
|
0,84
235,6
|
0,76
265,7
|
0,69
295,9
|
0,64
326,0
|
0,59
356,2
|
0,55
386,3
|
0,51
416,5
|
0,48
446,6
|
0,45
476,8
|
0,43
506,9
|
0,41
537,1
|
|

|
dc =
25 мм
Fa =
87,3 см2
|
-
|
-
|
-
|
1,39
145,4
|
1,20
178,2
|
1,05
210,9
|
0,94
243,6
|
0,85
276,4
|
0,77
309,1
|
0,71
341,8
|
0,65
374,6
|
0,61
407,3
|
0,57
440,1
|
0,53
472,8
|
0,50
505,5
|
0,47
538,3
|
0,45
571,0
|
|
dc = 32 мм
Fa =
103 см2
|
-
|
-
|
-
|
-
|
1,42
196,9
|
1,24
235,6
|
1,11
274,2
|
1,00
312,8
|
0,91
351,4
|
0,84
390,1
|
0,77
428,7
|
0,72
467,3
|
0,67
505,9
|
0,63
544,6
|
0,59
583,2
|
0,56
621,8
|
0,53
660,4
|
Продолжение табл. 78
|
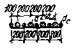
|
dc =
25 мм
Fa =
87,3 см2
|
-
|
-
|
-
|
1,34
152,3
|
1,16
185,0
|
1,03
217,7
|
0,92
250,5
|
0,83
283,2
|
0,76
315,9
|
0,70
348,7
|
0,64
381,4
|
0,60
414,2
|
0,56
446,9
|
0,53
479,6
|
0,49
512,4
|
0,47
545,1
|
0,44
577,8
|
|
dc =
32 мм
Fa = 103,0 см2
|
-
|
-
|
-
|
-
|
1,37
205,4
|
1,21
244,1
|
1,08
282,7
|
0,98
321,3
|
0,89
359,9
|
0,82
398,6
|
0,76
437,2
|
0,71
475,8
|
0,66
514,4
|
0,62
553,1
|
0,58
591,7
|
0,55
630,3
|
0,52
668,9
|
|
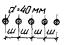
|
Ш = 200 мм
Fa =
75,4 см2
|
-
|
1,41
73,9
|
1,15
97,5
|
0,97
121,0
|
0,84
144,6
|
0,74
168,1
|
0,66
191,7
|
0,60
215,2
|
0,54
238,8
|
0,50
262,3
|
0,46
285,9
|
0,43
309,4
|
0,40
333,0
|
0,38
356.5
|
0,35
380,1
|
0,34
403,6
|
0,32
427,9
|
|
Ш = 150 мм
Fa =
83,8 см2
|
-
|
-
|
-
|
1,29
147,8
|
1,12
179,2
|
0,99
210,6
|
0,88
242,1
|
0,80
273,5
|
0,73
304,9
|
0,67
336,3
|
0,62
367,8
|
0,57
399,2
|
0,54
430,6
|
0,50
462,0
|
0,48
493,5
|
0,45
524,9
|
0,43
556,3
|
|
Ш = 100 мм
Fa = 125,7 см2
|
-
|
-
|
-
|
-
|
-
|
|
1,33
322,0
|
1,20
369,1
|
1,09
416,2
|
1,00
463,4
|
0,93
510,5
|
0,86
557,6
|
0,81
604,8
|
0,76
651,9
|
0,72
699,1
|
0,68
746,2
|
0,64
793,3
|
|
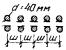
|
Ш = 200 мм
Fa =
125,7 см2
|
-
|
-
|
-
|
-
|
-
|
-
|
1,36
310,6
|
1,23
357,8
|
1,12
404,9
|
1,02
452,1
|
0,95
499,2
|
0,88
546,3
|
0,82
593,5
|
0,77
640,6
|
0,73
687,7
|
0,69
734,9
|
0,65
782,0
|
|
Ш = 150 мм
Fa =
167,6 см2
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
1,37
547,9
|
1,26
610,7
|
1,17
673,6
|
1,10
736,4
|
1,03
799,3
|
0,97
862,1
|
0,92
925,0
|
0,87
987,8
|
Примечание. Над чертой дано армирование μ, %; под чертой - соответствующая
несущая способность на изгиб М,
кН·м·10, плитных фундаментов, армированных арматурой класса А-II.
Таблица 79
|
Схема армирования
|
При толщине плитных фундаментов из бетона марки М
300, мм
|
|
400
|
500
|
600
|
700
|
800
|
900
|
1000
|
1100
|
1200
|
1300
|
1400
|
1500
|
1600
|
1700
|
1800
|
1900
|
2000
|
|

|
dc =
25 мм
Fa =
24,5 см2
|
0,69
22,8
|
0,54
29,7
|
0,44
36,7
|
0,37
43,7
|
0,32
50,7
|
0,28
57,7
|
0,25
64,7
|
0,23
71,6
|
0,21
8,6
|
0,19
85,6
|
0,18
92,6
|
0,16
99,6
|
0,15
106,5
|
0,14
113,5
|
0,13
120,5
|
0,13
127,5
|
0,12
134,5
|
|
dc =
32 мм
Fa =
40,2 см2
|
1,15
35,1
|
0,89
46,5
|
0,73
58,0
|
0,61
69,4
|
0,53
80,9
|
0,47
92,4
|
0,42
103,8
|
0,38
115,3
|
0,34
126,7
|
0,32
l38,2
|
0,29
149,6
|
0,27
161,1
|
0,25
172,6
|
0,24
184,0
|
0,22
195,5
|
0,21
206,9
|
0,20
218,4
|
|
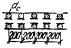
|
dc =
25 мм
Fa =
49,1 см2
|
1,46
39,7
|
1,12
53,7
|
0,91
67,7
|
0,77
81 ,7
|
0,66
95,7
|
0,58
109,7
|
0,52
123,7
|
0,47
137,7
|
0,43
151,7
|
0,39
165,7
|
0,36
179,7
|
0,34
193,6
|
0,31
207,6
|
0,30
221,6
|
0,28
235,6
|
0,26
249,6
|
0,25
263,6
|
|
dc =
32 мм
Fa =
80,4 см2
|
2,44
55,9
|
1,87
78,8
|
1,51
101,7
|
1,27
124,6
|
1,10
147,5
|
0,96
170,5
|
0,86
193,4
|
0,78
216,3
|
0,71
239,2
|
0,65
262,1
|
0,60
285,0
|
0,56
307,9
|
0,52
330,9
|
0,49
353,8
|
0,46
376,7
|
0,43
399,6
|
0,41
422,5
|
|
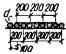
|
dc = 25 мм
Fa =
49,1 см2
|
1,39
42,0
|
1,08
56,0
|
0,88
70,0
|
0,75
84,0
|
0,65
98,0
|
0,57
112,0
|
0,51
126,0
|
0,46
140,0
|
0,42
154,0
|
0,39
168,0
|
0,36
182,0
|
0,33
196,0
|
0,31
209,9
|
0,29
223,9
|
0,28
237,9
|
0,26
251,9
|
0,25
265,9
|
|
dc =
32 мм
Fa = 80,4 см2
|
2,30
60,5
|
1,79
83,4
|
1,46
106,3
|
1,23
129,2
|
1,07
152,1
|
0,94
175,0
|
0,84
198,0
|
0,76
220,9
|
0,69
243,8
|
0,64
266,7
|
0,59
289,6
|
0,55
312,5
|
0,51
335,4
|
0,48
358,4
|
0,45
381,3
|
0,43
404,2
|
0,41
427,1
|
|

|
dc =
25 мм
Fa =
87,3 см2
|
2,67
58,2
|
2,04
83,1
|
1,65
108,0
|
1,39
132,0
|
1,20
157,7
|
1,05
182,6
|
0,94
207,5
|
0,85
232,4
|
0,77
257,2
|
0,71
282,1
|
0,65
307,0
|
0,61
331,9
|
0,57
356,8
|
0,53
381,6
|
0,50
406,5
|
0,47
431,4
|
0,45
456,3
|
|
dc =
32 мм
Fa =
103 см2
|
-
|
2,42
92,7
|
1,96
122,0
|
1,64
151,4
|
1,42
180,7
|
1,24
210,1
|
1,11
239,5
|
1,00
268,8
|
0,91
298,2
|
0,84
327,5
|
0,77
356,9
|
0,72
386,2
|
0,67
415,6
|
0,63
444,9
|
0,59
474,3
|
0,56
503,6
|
0,53
533,0
|
Продолжение табл. 79
|

|
dс = 25 мм
Fa
=87,3 см2
|
2,51
63.4
|
1,95
88,3
|
1,59
113,1
|
1,34
138,0
|
1,16
162,9
|
1,03
187,8
|
0,92
212,7
|
0,83
237,5
|
0,76
262,4
|
0,70
287,3
|
0,64
312,2
|
0,60
337,1
|
0,56
361,9
|
0,53
386,9
|
0,47
411,7
|
0,47
436,6
|
0,44
461,5
|
|
dс = 32 мм
Fа = 103 см2
|
-
|
2,30
99,1
|
1,88
128,5
|
1,59
157,8
|
1,37
187,2
|
1,21
216,5
|
1,08
245,9
|
0,98
275,3
|
0,89
304,6
|
0,82
334,0
|
0,76
362,3
|
0,71
392,7
|
0,66
422,0
|
0,62
451,4
|
0,58
480,7
|
0,55
510,1
|
0,52
539,4
|
|
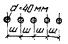
|
Ш = 200 мм
Fa
=75,4 см2
|
1,82
49,8
|
1,41
67,7
|
1,15
85,6
|
0,97
103,5
|
0,84
121,4
|
0,74
139,3
|
0,66
157,2
|
0,63
175,1
|
0,54
193,0
|
0,50
210,9
|
0,46
228,8
|
0,43
246,7
|
0,40
264,6
|
0,38
282,5
|
0,35
300,4
|
0,34
318,3
|
0,32
336,2
|
|
Ш = 150 мм
Fа = 83,8 см2
|
2,42
61,2
|
1,86
85,1
|
1,53
109,0
|
1,29
132,9
|
1,12
156,8
|
0,99
180,6
|
0,88
204,5
|
0,87
228,4
|
0,73
252,3
|
0,67
276,2
|
0,62
300,1
|
0,57
323,9
|
0,54
347,8
|
0,50
371,7
|
0,45
395,6
|
0,45
419,5
|
0,43
443,3
|
|
Ш = 100 мм
Fа = 125,7 см2
|
-
|
-
|
2,30
147,7
|
1,94
183,5
|
1,68
279,3
|
1,48
255,1
|
1,33
291,0
|
1,20
326,8
|
1,09
362,6
|
1,00
398,4
|
0,92
434,3
|
0,86
470,1
|
0,81
505,9
|
0,76
541,7
|
0,72
577,6
|
0,68
613,4
|
0,64
649,2
|
|

|
Ш = 200 мм
Fа = 125,7 см2
|
-
|
-
|
2,41
139,1
|
2,02
174,9
|
1,74
270,7
|
1,53
246,5
|
1,36
282,4
|
1,23
318,2
|
1,12
354,0
|
1,02
389,8
|
0,95
425,7
|
0,88
461,5
|
0,82
497,3
|
0,77
533,1
|
0,73
569,0
|
0,69
604,8
|
0,65
640,6
|
|
Ш = 150 мм
Fa = 167,6 см2
|
-
|
-
|
-
|
2,69
212,1
|
2,32
289,8
|
2,04
307,6
|
1,81
355,4
|
1,64
403,1
|
1,49
450,9
|
1,37
498,7
|
1,26
546,4
|
1,17
594,2
|
1,10
642,0
|
1,03
689,7
|
0,97
737,5
|
0,92
785,3
|
0,87
833,0
|
Примечание. Над чертой дано армирование μ, %; под чертой - соответствующая
несущая способность на изгиб М,
кН·м·10, плитных фундаментов, армированных арматурой класса А-II.
Таблица 80
|
Схема армирования
|
При толщине плитных фундаментов, из бетона марки М
300, мм
|
|
|
400
|
500
|
600
|
700
|
800
|
900
|
1000
|
1100
|
1200
|
1300
|
1400
|
1500
|
1600
|
1700
|
1800
|
1900
|
2000
|
|

|
dс = 25 мм
Fа = 24,5 см2
|
0,69
29,2
|
0,54
38,4
|
0,44
47,6
|
0,37
56,8
|
0,32
66,0
|
0,28
75,1
|
0,25
84,3
|
0,23
93,5
|
0,21
102,7
|
0,19
111,9
|
0,18
121,1
|
0,16
130,3
|
0,15
139,5
|
0,14
148,6
|
0,13
157,8
|
0,13
167,0
|
0,12
176,2
|
|
dc =
32 мм
Fa =
40,2 см2
|
1,15
44,1
|
0,89
59,2
|
0,73
74,3
|
0,61
89,4
|
0,53
104,4
|
0,47
119,5
|
0,42
134,6
|
0,38
149,7
|
0,34
164,7
|
0,32
179,8
|
0,29
194,9
|
0,27
210,0
|
0,25
225,0
|
0,24
240,1
|
0,22
255,2
|
0,21
270,3
|
0,20
286,3
|
|

|
dc =
25 мм
Fa =
49,1 см2
|
1,46
49,3
|
1,12
67,7
|
0,91
86,1
|
0,77
104,5
|
0,66
122,9
|
0,58
141,3
|
0,52
159,7
|
0,47
178,1
|
0,43
196,6
|
0,39
215,0
|
0,36
233,4
|
0,34
251,8
|
0,31
270,2
|
0,30
288,6
|
0,28
307,0
|
0,26
325,4
|
0,25
343,9
|
|
dс = 32 мм
Fa =
80,4 см2
|
-
|
1,87
95,6
|
1,51
125,8
|
1,27
155,9
|
1,10
186,1
|
0,96
216,2
|
0,86
246,4
|
0,78
276,5
|
0,71
306,7
|
0,65
336,8
|
0,60
367,0
|
0,56
397,1
|
0,52
427,3
|
0,49
457,4
|
0,46
487,6
|
0,43
517,7
|
0,41
547,9
|
|
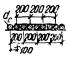
|
dс = 25 мм
Fa =
49,1 см2
|
1,39
52,3
|
1,08
70,7
|
0,88
89,1
|
0,75
107,5
|
0,65
125,9
|
0,57
144,4
|
0,51
162,8
|
0,46
181,2
|
0,42
199,6
|
0,39
218,0
|
0,36
236,4
|
0,33
254,8
|
0,31
273,2
|
0,29
291,7
|
0,28
310,1
|
0,26
328,5
|
0,25
346,9
|
|
dc =
32 мм
Fа = 80,4 см2
|
-
|
1,79
101,7
|
1,46
131,8
|
1,23
162,0
|
1,07
192,1
|
0,94
222,3
|
0,84
252,4
|
0,76
282,6
|
0,69
312,7
|
0,64
342,9
|
0,59
373,0
|
0,55
403,2
|
0,51
433,3
|
0,43
463,5
|
0,45
493,6
|
0,43
523,8
|
0,41
553,9
|
|

|
dc =
25 мм
Fa =
87,3 см2
|
-
|
-
|
1,65
132,5
|
1,39
165,3
|
1,20
198,0
|
1,05
230,7
|
0,94
263,5
|
0,85
296,2
|
0,77
329,0
|
0,71
361,7
|
0,65
394,4
|
0,61
427,2
|
0,57
459,9
|
0,53
492,6
|
0,50
525,4
|
0,47
558,1
|
0,45
590,9
|
|
dc =
32 мм
Fа = 103 см2
|
|
-
|
1,96
147,3
|
1,64
186,0
|
1,42
224,6
|
1,24
263,2
|
1,11
301,8
|
1,00
340,5
|
0,91
379,1
|
0,84
417,7
|
0,77
456,3
|
0,72
495,0
|
0,67
533,6
|
0,63
572,2
|
0,59
610,8
|
0,56
649,5
|
0,53
688,1
|
Продолжение табл. 80
|

|
dc =
25 мм
Fa =87,3 см2
|
-
|
1,95
106,6
|
1,59
139,4
|
1,34
172,1
|
1,16
204,8
|
1,03
237,6
|
0,92
270,3
|
0,83
303,1
|
0,76
335,8
|
0,70
368,5
|
0,64
401,3
|
0,60
434,0
|
0,56
466,7
|
0,53
499,5
|
0,49
532,2
|
0,47
565,0
|
0,44
597,7
|
|
dc =
32 мм
Fa = 103 см2
|
-
|
-
|
1,88
155,8
|
1,59
194,4
|
1,37
233,1
|
1,21
271,7
|
1,08
310,3
|
0,98
348,9
|
0,89
387,6
|
0,82
426,2
|
0,76
464,8
|
0,71
503,4
|
0,66
542,1
|
0,62
580,7
|
0,58
619,3
|
0,55
657,9
|
0,52
696,6
|
|
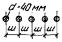
|
Ш = 200 мм
Fа=75.4 см2 а
|
1,82
60,7
|
1,41
84,2
|
1,15
107,8
|
0,97
131,3
|
0,84
154,9
|
0,74
178,4
|
0,66
202,0
|
0,60
225,5
|
0,54
249,1
|
0,50
272,6
|
0,46
296,2
|
0,43
319,7
|
0,40
343,3
|
0,38
366,8
|
0,35
390,4
|
0,34
413,9
|
0,32
437,5
|
|
Ш = 150 мм
Fа =83,8 см2
|
-
|
1,88
103,2
|
1,53
134,6
|
1,29
166,1
|
1,12
197,5
|
0,99
228,9
|
0,88
260,3
|
0,80
291,8
|
0,73
323,2
|
0,67
354,6
|
0,62
386,0
|
0,57
417,5
|
0,54
448,9
|
0,50
480,3
|
0,48
511,7
|
0,45
547,2
|
0,43
574,6
|
|
Ш = 100 мм
Fa =
125,7 см2
|
-
|
-
|
-
|
1,94
221,7
|
1,68
268,8
|
1,48
316,0
|
1,33
363,1
|
1,20
410,2
|
1,09
457,4
|
1,00
504,5
|
0,93
551,7
|
0,86
598,8
|
0,81
645,9
|
0,76
693,1
|
0,72
740,2
|
0,68
787,3
|
0,64
834,5
|
|

|
Ш = 200 мм
Fa =
125,7 см2
|
-
|
-
|
-
|
2,02
210,4
|
1,74
257,5
|
1,53
304,7
|
1,36
351,8
|
1,23
398,9
|
1,12
446,1
|
1,02
493,2
|
0,95
540,3
|
0,88
587,5
|
0,82
634,6
|
0,77
681,8
|
0,73
728,9
|
0,69
776,0
|
0,65
823,2
|
|
Ш = 150 мм
Fa =
167,6 см2
|
-
|
-
|
-
|
-
|
-
|
-
|
1,81
432,5
|
1,64
495,3
|
1,49
558,2
|
1,37
621,0
|
1,26
683,9
|
1,17
746,7
|
1,10
809,6
|
1,03
872,4
|
0,97
935,3
|
0,92
998,1
|
0,87
1061,0
|
Примечание. Над чертой дано армирование μ, %: под чертой - соответствующая
несущая способность на изгиб М,
кН·м·10, плитных фундаментов, армированных арматурой класса А-III.
6.5. Армирование фундаментных плит следует производить в двух зонах: нижней
и верхней. Каждая зона должна иметь рабочую арматуру в двух направлениях.
6.6. Шаг арматуры верхней зоны следует принимать не менее
200 мм, шаг арматуры нижней зоны допускается в обоснованных случаях уменьшать
до 100 мм.
6.7. Минимальную толщину плиты следует назначать, исходя
из условия пп. 3.30 и 3.32 СНиП по проектированию бетонных и железобетонных
конструкций. Минимальные проценты армирования назначать:
для бетона М 200 - 0,1;
для бетона М 300 - 0,15.
6.8. Расположение арматуры в плане фундамента должно
назначаться в соответствии с огибающими эпюрами изгибающих моментов,
построенными в направлении длины и ширины плитного фундамента прямоугольной
формы.
Армирование обоих направлений верхней и
нижней зоны рекомендуется расчленять на основное непрерывное и дополнительное
локальное.
Непрерывное армирование нижней зоны
рекомендуется назначать по величине армирования участков фундамента между
опирающимися на него колоннами. Площадь сечения этой арматуры назначают либо по
расчету, либо конструктивно согласно указаниям настоящего раздела.
Дополнительную арматуру нижней зоны предусматривают под колоннами, участками
повышенной жесткости и т.п. Площадь сечения этой арматуры определяют по расчету
соответствующих сечений фундамента, за вычетом площади сечения непрерывного
армирования.
Площадь сечения непрерывного армирования
верхней зоны назначают, как правило, по конструктивным требованиям.
Дополнительную арматуру (если она требуется) назначают по расчету в местах
максимальных отрицательных моментов.
Круглый плитный фундамент рекомендуется
армировать либо в направлениях взаимно перпендикулярных диаметров, либо в
радиальном и тангенциальном направлениях.
Первый способ предпочтительнее при
армировании фундаментов, нагруженных прямоугольной сеткой колонн.
Второй способ может быть рекомендован для
фундаментов, которые нагружены либо по кольцевому сечению (дымовые трубы,
круглые силосы, стены которых доходят до фундамента, и т.п.), либо радиальной
сеткой колонн.
6.9. Каждая зона армирования фундамента должна состоять не более чем из
четырех слоев сеток (рис. 67).
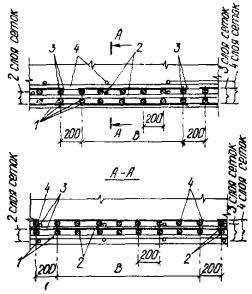
Рис. 67. Многослойное армирование плиты унифицированными
сетками при шаге рабочих стержней 200 мм
1-4 - сетки 1,
2, 3, 4-го слоя соответственно (В
- ширина сетки)
Для увеличения несущей способности
фундамента в нижних слоях обоих направлений нижней зоны допускается укладка
двух сеток (одной на другую) с расположением рабочих стержней в одной плоскости
и получением шага между ними, равным 100 мм (рис. 68).

Рис.
68. Многослойное армирование плиты унифицированными сетками при шаге рабочих
стержней нижнего слоя 100 мм
1-4 - сетки 1, 2, 3, 4-го слоя
соответственно
6.10. Стык сеток в рабочем направлении должен
осуществляться внахлестку. При этом одна из сеток в пределах стыка ие должна
иметь монтажных стержней.
6.11. Площадь рабочей арматуры, стыкуемой в одном сечении,
не должна превышать для гладких стержней - 25 %, для арматуры периодического
профиля - 50 %.
6.12. Принципиальная схема раскладки унифицированных сеток
армирования прямоугольных фундаментов приведена на рис. 69, круглых - на рис.
70.
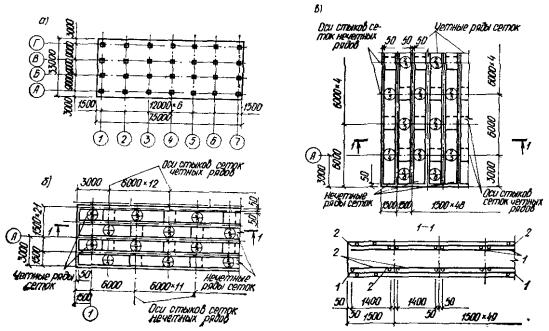
Рис.
69. Схема раскладки унифицированных сеток армирования прямоугольной плиты
а - план плитного фундамента; б - план раскладки сеток первого слоя
нижней зоны и второго слоя верхней зоны; в - план раскладки сеток второго слоя нижней зоны и первого слоя
верхней зоны; 1 - унифицированные сетки вдоль цифровых осей; 2 - унифицированные сетки укороченные

Рис. 70. Армирование круглой плиты фундамента
в радиальном и тангенциальном направлениях
6.13. Обеспечение проектного положения арматуры верхней
зоны рекомендуется осуществлять:
при толщине фундамента до 1000 мм
включительно - с помощью поддерживающих каркасов;
при толщине более 1000 мм - с помощью
специальных поддерживающих конструкций, выполняемых из прокатных профилей.
Шаг поддерживающих каркасов назначают,
исходя из монтажных нагрузок и диаметра рабочей арматуры.
При обычных монтажных нагрузках шаг
поддерживающих каркасов принимают:
при диаметре рабочих стержней до 16 мм -
1000 мм;
при диаметре рабочих стержней
от 18 до 25 мм - 2000 мм;
при диаметре рабочих стержней
свыше 25 мм - 3000 мм.
6.14. Площадь конструктивной арматуры назначают по
минимальному проценту армирования, но не менее 20 % максимальной площади рабочей арматуры того же направления.
Диаметр стержней конструктивной арматуры должен приниматься не менее 12 мм.
6.15. Расстояние между осями отдельных стержней рабочей
арматуры следует назначать из расчета не менее трех стержней на 1 м ширины
сечения фундамента и не менее величины, предусмотренной главой СНиП по
проектированию бетонных и железобетонных конструкций с учетом условий
производства работ и требований унификации.
6.16. При армировании отдельными стержнями стержни рабочей
арматуры диаметром до 20 мм соединяют внахлестку (без сварки).
Стержни диаметром 20 мм и более следует
соединять с помощью сварки в соответствии с указаниями главы СНиП по
проектированию бетонных и железобетонных конструкций.
6.17. Температурно-усадочные швы назначают для обеспечения
свободы температурных деформаций и для исключения перенапряжений в массивах
фундаментов от усадочных деформаций бетона.
Расстояние между швами монолитных
фундаментов не должно превышать 40 м.
Если фундаменты не могут быть разделены
на участки длиной менее 40 м, то необходимо предусматривать временные усадочные
швы шириной от 0,7 до 1,2 м. В этих случаях из массива фундаментов с обеих
сторон временного шва (в уровне подошвы и верхней поверхности фундамента)
должна быть выпущена рабочая арматура, которую, спустя 3-4 недели после
бетонирования фундаментов необходимо соединить сваркой с накладными стержнями,
а шов заполнить бетоном той же марки.
6.18. Толщину защитного слоя нижней арматуры при наличии
бетонной подготовки следует принимать равной 35
мм. Для агрессивных сред
толщину защитного слоя принимают согласно указаниям главы СНиП на защиту
строительных конструкций от коррозии.
7. ТРЕБОВАНИЯ К
ИЗМЕРЕНИЯМ ОСАДОК, СДВИГОВ И КРЕНОВ ФУНДАМЕНТОВ ПЛИТ
7.1. Работы по организации и проведению наблюдений за
деформациями оснований и фундаментов (осадки, подъемы, сдвиги, крены и т. д.)
зданий и сооружений проводят в соответствии с указанием «Руководства по
наблюдениям за деформациями оснований и фундаментов зданий и сооружений» (М.,
Стройиздат, 1975).
7.2. Организация, проектирующая сооружение, совместно с
организацией, производящей измерения, составляют рабочую программу по
наблюдениям за деформациями оснований и фундаментов зданий и сооружений, в
которой подробно излагают выбранную методику измерений, обеспечивающую
необходимую и достаточную точность определения величин деформаций, указывают
конструкции и места расположения геодезических знаков, дают перечень рабочих
инструментов.
7.3. Календарный план, прикладываемый к рабочей программе,
должен отражать периодичность проведения циклов измерений как в строительный,
так и в эксплуатационный период.
7.4. Наблюдения за осадками и деформациями фундаментов
следует прекратить, если в течение года измеренная величина деформаций
находится в пределах точности измерений, и возобновить в случае появления
трещин в несущих конструкциях сооружения, а также резкого изменения условий
работы (увеличения нагрузок, подъема уровня грунтовых вод и т.п.).
7.5. Измерение осадок фундаментных плит производят
геометрическим нивелированием 1 класса, при котором допускается средняя
квадратичная ошибка ±1 мм.
Для измерения осадок фундаментной плиты и
слоев грунта в плиту, колонны, подколонники и стены подвала закладывают
геодезические знаки - стенные и плитные марки, а в грунты - неподвижные
исходные геодезические знаки - глубинные реперы.
Под абсолютной осадкой марок понимают
разность отметок марки и исходного репера.
Существенное влияние на точность
измерений оказывают принятая конструкция геодезических знаков и правильность их
установки.
7.6. Стенные марки закрытого типа, состоящие из корпуса (рис. 71) и крышки
(рис. 72), изготовляют из стали марки Ст3 (ГОСТ 380-71*)
с точностью обработки Ñ4(Ñ). Корпус марки заподлицо бетонируют в стену или
колонну.

Рис.
71. Корпус стенной марки
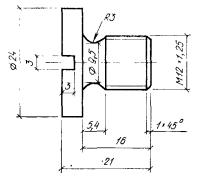
Рис.
72. Крышка стенной марки
При производстве геодезических работ в
отверстие марки вместо крышки должен быть ввинчен шаровой болт (рис. 73),
который служит фиксированной точкой. Болт изготовляют из стали марки Ст3 (ГОСТ
380-71* с точностью обработки Ñ5(Ñ).

Рис.
73. Шаровой болт для геодезических работ
При большой толщине конструкции чистого
пола подвала технического подполья многоэтажного здания плитную марку (рис. 74)
следует крепить к защитному металлическому патрубку, который приваривают к
арматуре и снабжают крышкой. Поверхность крышки должна находиться на уровне чистого
пола подвала или технического подполья. Головку марки приваривают к днищу на
глубине не более 15 см от поверхности крышки. Внутренний диаметр патрубка
должен быть не менее 100 м для свободной установки пяты нивелирной рейки на
головку марки. Полусферическую поверхность головки марки в целях предохранения
от коррозии покрывают защитным слоем тавота.

Рис.
74. Плитная марка
1 -
крышка; 2 - кольцо из трубы
диаметром 159 мм, толщиной 4,5 мм (ГОСТ 10704-76*);
3 - верхний патрубок из трубы
диаметром 114 мм, толщиной 4 мм, длиной 124 мм (ГОСТ 10704-76*);
4 - днище диаметром 135 мм,
толщиной 6 мм, из стали Ст3 (приваривается к верхней арматуре); 5 -
нижний патрубок из трубы диаметром 114 мм, толщиной 4 мм, длиной А (ГОСТ 10704-76*);
6 - полусфера радиусом 40 мм из
стали Ст5
7.7. Глубинный репер (рис. 75) для наблюдения за осадками зданий и
сооружений состоит из следующих конструктивных элементов: реперной трубы,
башмака, реперной головки, реперного колодца, защитной трубы, сальника.
Реперная труба 7 состоит из соединенных
муфтами стальных газовых или буровых труб с наружным диаметром 89 мм. Нижний
конец реперной трубы запрессовывают в стальной башмак 12, обетонируемый в скважине на такой глубине, на которой можно
считать грунт практически неподвижным и не подвергающимся деформациям. Тип
башмака выбирают в зависимости от вида грунта основания репера: для скальных,
крупнообломочных н песчаных грунтов - конусный (рис. 75), для глинистых -
лопастной. На верхнем конце репера устраивают специальную реперную головку 4, изготовляемую из бронзы или
нержавеющей стали, со шлифованной полусферической поверхностью диаметром 30 -
40 мм.

Рис. 75. Глубинный репер
а - глубинный репер в сборе; б - стальная крышка защитной трубы; в - реперная головка; г - сальник
Реперный колодец имеет кирпичные или
железобетонные стенки 2, бетонное дно 14
и чугунный люк 18.
Колодец предохраняет верхнюю часть репера
от смешения из-за температурных изменений, пучения грунтов, промерзания, а
также случайных воздействий при каких-либо работах вблизи репера. Во избежание
передачи возможных вертикальных смещений колодца на реперную трубу защитную
трубу 8 в месте прохода через
бетонный пол обертывают двойным слоем толя 9.
Дно колодца должно быть выше уровня
грунтовых вод и на 0,5 м ниже глубины промерзания грунта. Расстояние между
низом чугунной крышки и реперной головкой из условия удобства нивелировки
принимают равным 20 см. В люке помимо верхней чугунной крышки устраивают еще
нижнюю деревянную крышку 16, обитую
войлоком, с целью уменьшения колебаний температуры в колодце; кроме того,
колодец до уровня реперной головки засыпают сухим шлаком 15 или другим теплоизоляционным
материалом.
Защитная труба 8 состоит из соединенных муфтами обсадных стальных труб с
наружным диаметром 168 мм и толщиной стенок 7 мм. Защитная труба предохраняет
реперную трубу от возможных смещений, вызываемых сжатием или набуханием
окружающего грунта. Верхний конец ее закрывают стальной крышкой 3.
Для центрирования реперной трубы
относительно защитной применяются стальные шпильки 5 через 4-6 м по высоте.
Сальник 11 состоит из стального цилиндра, заполненного сальниковой
набивкой с тавотом или тяжелым смазочным маслом. Он наглухо закреплен с нижним
концом защитной трубы и служит препятствием для проникания ила в пространство
между реперной и защитной трубами.
Для установки глубинного репера проводят
следующие работы: вспомогательные (выбор местоположения глубинного репера и
согласование его с организациями, ведающими подземным хозяйством, а также
изготовление репера в мастерских строительства и бурение скважины) и основные
(сборка репера на поверхности земли и спуск его по частям в пробуренную
скважину).
Вспомогательные работы включают
определение общей длины репера, установление размеров каждого отрезка (звена)
защитных и реперных труб. При этом все соединения реперных труб проектируют
так, чтобы их муфты приходились на высоте 0,5-1 м над такими же соединениями
защитных труб.
Репер изготавливают из прямых новых или
бывших в употреблении труб; не допускается применение труб изогнутых, сильно
заржавевших, с раковинами, а также с вмятинами, со сбитой нарезкой и другими
дефектами.
Реперные и защитные трубы следует
предохранять от коррозии, для чего их очищают от ржавчины и покрывают
асфальтовым лаком. Затем производят опорную сборку репера, во время которой все
сопрягаемые стыки пригоняют и нумеруют.
В намеченном месте для установки
глубинного репера бурят скважину диаметром 325 мм, причем особое внимание
должно быть обращено на ее вертикальность. Допускаемое отклонение скважины от
вертикали на всю ее длину не должно превышать 0,5 диаметра буровых труб.
Основные работы начинают со сборки репера
на поверхности земли.
До окончания буровых работ реперную
установку подносят к скважине и подготавливают к спуску. На нижний конец
реперной трубы надевают сальник, производят набивку его и сжатие набивки нижним
кольцом. Затем укрепляют направляющие планки 10, надевают защитную трубу и приваривают ее к верхнему кольцу
сальника.
Перед опусканием реперной установки в
скважину во избежание затруднений по поднятию обсадных труб, которыми
производилось бурение, необходимо эти трубы слегка сдвинуть с места.
На дно скважины непосредственно перед
спуском реперной и защитной труб опускают цементный раствор состава 1:3 в
объеме, достаточном для наполнения пространства между башмаком и стенками
скважины, до уровня фланца 13. Защитную
трубу опускают вниз, слегка ударяя по фланцу.
После опускания всей колонны реперных и
защитных труб из скважины извлекают буровые обсадные трубы, а пространство
между стенками скважины заполняют песком, затем устраивают бетонное дно
реперного колодца и выкладывают нижнюю часть стенки. После приварки 6 (или припайки) реперной головки 4 заканчивают кладку колодца,
засыпают пазухи котлована грунтом с плотным трамбованием 1, устанавливают чугунный люк с крышкой,
планируют поверхность земли вокруг люка и устраивают бетонный отлив или
отмостку вокруг колодца 17. Затем
колодец засыпают сухим шлаком 15.
Об установке репера следует составить
акт, в котором указать:
время окончания работ по установке
репера;
координаты реперного колодца, отнесенные
к капитальным объектам (не подлежащим сносу в срок службы репера);
геологический разрез буровой скважины, в
которой был установлен репер, с указанием отметки башмака;
акт сдачи-приемки репера на хранение
соответствующим организациям;
отметку головки репера, определенную от
ближайшей из точек геодезической высотной сети не ранее, чем через десять дней
после установки репера.
О присвоении реперу высотной отметки
также составляют акт, в котором указывают:
время передачи отметки;
местоположение и отметку исходного
местного репера;
какими инструментами передана отметка;
отметку реперной головки с вероятной
погрешностью.
7.8. Для организации наблюдений за осадками плитного фундамента необходимо
выполнить следующие работы:
разработать проект закладки марок в
плитный фундамент, подколонники, колонны и стены здания или сооружения; для
этого нужно нанести на план каркасного здания по ортогональной сетке,
проходящей через центры колонн и середины расстояний между колоннами, а также
по контуру и в характерных точках кольцевых и круглых плитных фундаментов
сооружений башенного типа, места закладки марок с учетом возможности доступа к
ним и визуальной передачи отметки на марки в период эксплуатации здания или
сооружения (рис. 76);
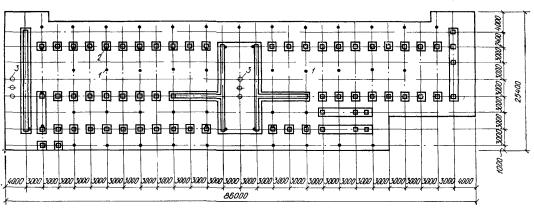
Рис. 76. Схема расположения осадочных марок
на плане плитного фундамента многоэтажного административного здания (стенные
марки показаны условно)
1 - плитная марка; 2 - стенная; 3 - глубинная
марки в плите обязательно следует
дублировать марками в колоннах и стенах; на чертежах нужно дать конструкции
стенных и плитных марок. При этом защитную трубу плитной марки следует
назначить такой длины, чтобы крышка марки находилась на уровне верха пола
подвала, технического подполья или первого этажа. Если плитная марка,
закладываемая на консольном участке плиты, попадает за пределы контура здания,
т. е. выводится на дневную поверхность грунта, то верхнюю часть марки защищают
колодцем, аналогичным реперному;
на генеральном плане участка
строительства нанести и согласовать с горгеотрестом места расположения
глубинных реперов, выбираемые с учетом следующих условий:
реперы должны закладываться на расстояния
50 - 160 м от здания вне проездов и складских помещений и по возможности с
разных сторон здания;
к реперам должен быть обеспечен удобный и
беспрепятственный подход, а также возможность визуальной передачи отметки в
подвал здания;
реперы рекомендуется закладывать в
газонах и скверах в местах, где отсутствуют подземные коммуникации;
число реперов должно быть не менее двух.
На отдельном чертеже следует показать
конструкцию глубинного репера. При этом глубину заложения репера от подошвы
фундамента нужно принимать: до слоя скального грунта толщиной не менее 5 м,
если этот грунт залегает в нижней части сжимаемой толщи; меньшей или равной 25
м, если скальный грунт находится на большей глубине, с тем, чтобы заделать
репер в прочные грунты достаточной толщины с модулем деформации порядка 40-50 МПа.
7.9. Необходимо предусмотреть мероприятия по обеспечению
сохранности плитных марок и реперов на весь период строительства и эксплуатации
до стабилизации осадок.
7.10. Детали плитных марок и реперов следует изготовлять в
заводских условиях по утвержденным проектной организацией чертежам.
7.11. Глубинные реперы должна устанавливать специализированная
организация, например Фундаментпроект, по договору с заказчиком.
7.12. Стоимость изготовления, закладки марок, установки
глубинных реперов, а также наблюдений за осадками должна устанавливаться по
единым утвержденным расценкам и включаться в смету на устройство плитного
фундамента.
7.13. Наблюдения за осадками следует осуществлять
специализированной геодезической службой (проектной организации, горгеотреста и
др.) при консультации и методической помощи НИИОСП или Фундаментпроекта.
7.14. В сложных случаях (при существенной неоднородности
основания в плане, наличии в основании слоев слабых, сильносжимаемых грунтов и
т.д.) для ответственных сооружений, типовых плит, закладываемых в различных
грунтовых условиях, для накопления сведений по деформациям оснований под
нагрузкой и совершенствования методов расчета плитных фундаментов необходимо
предусмотреть измерение послойных деформаций грунтов оснований.
Для этой цели в пределах контура
фундамента в крайних и средних зонах закладываются глубинные марки. Конструкция
глубинных марок аналогична глубинным реперам с той лишь разницей, что верхняя
часть глубинной марки, не выходящая за пределы контура фундамента,
предохраняется защитной трубой, прорезающей фундамент и конструкцию пола
подвала. Для установки глубинной марки в бетонной подготовке оставляется
гнездо, в которое при монтаже арматуры устанавливается труба-кондуктор
диаметром 427 мм. После окончания бетонирования фундамента до монтажа
перекрытия подвала или технического подполья в трубе-кондукторе бурится
скважина, а затем монтируется глубинная марка.
Глубинные марки обычно располагают
группами по 3-4 шт. Места закладки глубинных марок показывают на плане
размещения плитных марок. Длину глубинных марок выбирают таким образом, чтобы
по их осадкам можно было оценить осадки наиболее характерных слоев грунта,
установить, на какой глубине происходит, в основном, затухание осадки основания
и проверить правильность определения расчетной глубины сжимаемой толщи
основания.
7.15. Измерения осадок марок следует начинать сразу после
окончания бетонирования плитного фундамента и продолжать во время строительства
здания по мере роста нагрузок, а также после сдачи здания в эксплуатацию до
наступления стабилизации осадок.
Циклы наблюдений выполняют в то время,
когда нагрузка на основание составляет 10, 20, 30,...,100 % веса здания, т.е. не менее двух раз в год,
считая продолжительность строительства многоэтажного здания, а также сооружения
башенного типа равной 2 - 3 годам.
Повторность циклов наблюдений после сдачи
здания в эксплуатацию зависит от скорости затухания осадок.
7.16. Суммарные осадки марок, полученные после каждого
цикла наблюдений, наносят на план фундамента по сечениям в виде эпюр
перемещения марок. Кроме того, по полученным осадкам наиболее характерных точек
фундамента строят графики роста осадок марок во времени и одновременно наносят
графики изменения во времени среднего давления на основание, как показано на
рис. 77, для фундамента здания института Гидропроект, чтобы установить скорость
изменения осадок во времени и связь между напряжениями и деформациями
основания.

Рис. 77. Осадки марок и среднее давление на
грунт
1 - марка в центре плиты; 2 - марка в краевой зоне плиты
7.17. Осадку плитного фундамента можно считать
стабилизированной, если скорость ее роста не превышает 1 мм в год.
7.18. Измерения сдвигов фундаментов зданий и сооружений
должны выполняться следующими методами: створа, триангуляции, направлений и
комбинированным.
7.19. Для проведения наблюдений за сдвигами допускается
использовать любые теодолиты с накладными уровнями, алиниометры, лазеры,
фототеодолиты, клинометры и другие геодезические инструменты. Поверка и
юстировка инструментов выполняется по соответствующим инструкциям.
7.20. Перед проведением наблюдений выбирают места и
конструкцию исходных и наблюдаемых знаков.
Исходные (опорные, контрольные и
ориентирные) знаки необходимо закладывать вне зоны давления от сооружения, в
стороне от оползневых склонов и проездов. Каждый знак должен быть удобным для
подхода с инструментом.
В качестве наблюдаемых знаков следует
использовать подвижные и неподвижные визирные цели, а также марки.
7.21. Опорные знаки служат для установки и центровки
теодолита. Они могут быть выступающими над землей (рис. 78) и скрытыми (рис.
79).
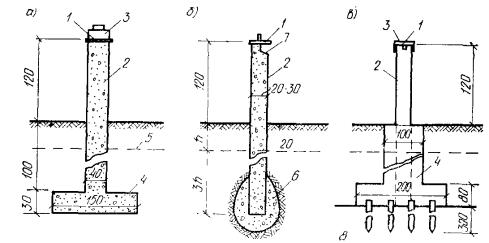
Рис.
78. Опорные знаки, выступающие над землей
а -
опорный знак из железобетона с плитным
фундаментом; б - опорный
знак - металлическая труба, заполненная железобетоном с бетонным башмаком; в - опорный знак из железобетона со
свайным фундаментом, устанавливаемый в слабых грунтах; 1 - центрировочное устройство; 2 - железобетонный или металлический наблюдательный столб; 3 - крышка; 4 - железобетонный фундамент; 5 - горизонт наибольшего
промерзания грунта; 6 - бетонный
башмак; 7 - отверстие для закрепления теодолита; 8 - сваи

Рис.
79. Скрытые опорные знаки
а - опорный знак, устанавливаемый
бурением; б - опорный
знак, устанавливаемый котлованным способом; 1 - головка знака с нарезным крестом; 2 - металлическая труба диаметром 5 см; 3 - отмостка; 4- диафрагма; 5 - защитная труба с
крышкой; 6 - башмак; 7 -
сальник; 8 - железобетонный
пилон квадратного сечения (вверху 15×15 см, внизу 30×30 см); 9 - смотровой колодец с люком; 10 - теплоизоляционная засыпка; 11 -
гидроизоляция; 12 -
фундаментная плита 50×50 см
Скрытые опорные знаки
применяются только тогда, когда запрещена установка выступающих знаков, так как
при использовании скрытых знаков возможны дополнительные ошибки измерений из-за
неточности центрирования.
Опорные знаки в виде кирпичных,
металлических, железобетонных столбов устанавливают котлованным способом при
низком уровне грунтовых вод (более 3 м). В случае высокого уровня грунтовых вод
опорные знаки применяют трубчатой конструкции и закладывают бурением.
В верхней части опорного знака для
установки теодолита имеется центрировочное устройство (рис. 80), на которое надевается крышка для
защиты знака от атмосферных воздействий (дождя, снега и т.п.). Опорные знаки
должны также иметь ограждающие устройства для обеспечения их сохранности и
неподвижности.

Рис. 80. Центрировочные устройства
1 -
металлический диск-столик; 2 -
коническая втулка; 3 - борозды;
V-образной формы под
углом 120° шириной 5-6 мм,
глубиной 4-5 мм; 4 -
металлическая пластина; 5 - латунный стержень с резьбой станового винта
теодолита
В качестве опорных знаков допускается
использовать глубинные репера, если они имеют на своей головке специальную
насечку в виде креста, а также пункты государственной триангуляции,
полигонометрии. В особых случаях для поднятия знака над поверхностью земли
допускается установка опорных знаков на крышах устойчивых сооружений.
Устойчивость опорных знаков должна
проверяться взаимной привязкой и при необходимости привязкой к контрольным
опорным знакам.
7.22. Контрольные знаки имеют конструкцию, аналогичную
исходным опорным знакам (см. рис. 78, 79), но их устанавливают в более надежных
местах и на прочных грунтах, так как к их устойчивости предъявляются повышенные
требования.
7.23. Ориентирными знаками могут служить удаленные пункты
триангуляции I и II класса, удобные для визирования точек зданий и
сооружений (шпили, колокольни церквей, радиомачты, телевышки и т.д.).
7.24. Конструкции неподвижных визирных целей допускаются
различные, но все они должны иметь плоские металлические щитки с разнообразными
фигурами в виде крестов или цилиндрических колец, закрепленные в подставках,
которые опираются на опорную плиту или подпятники, заделанные в головке столба.
Марки с визирными целями, устанавливаемые
на сооружении, приведены на рис. 81. В качестве наблюдаемых марок допускается
также применять марки, конструктивно похожие на скрытые нивелирные марки (см. рис. 71, 74).

Рис. 81. Неподвижные марки с визирными
целями, наглухо устанавливаемые на сооружении
а - марки, устанавливаемые в стене; б - марки, устанавливаемые в фундаменте
сооружения
7.25. Подвижные визирные цели, устанавливаемые на
наблюдаемые марки, имеют щиток с визирной целью, перемещаемый с помощью
микрометренного винта. Величина перемещения определяется по шкале микрометра с
точностью до 0,1 мм.
Перед началом работ у подвижных визирных
целей определяют место нуля цели (МО). (Отсчет по шкале микрометра, при котором
вертикальная ось визирной цели совпадает с вертикальной осью вращения марки).
Для определения МО в 10 - 30 м от марки
устанавливают теодолит, наводят его трубу на ось визирной цели и берут отсчеты
по микрометру, затем марку поворачивают на 180°, микрометренным винтом
передвигают визирную цель до совпадения с вертикальной осью теодолита и снова
производят отсчет. Полусумма отсчетов дает МО марки. Таких приемов делают пять
при каждом круге инструмента. За МО принимается среднеарифметическое из 10
отсчетов.
7.26. Наблюдаемые знаки должны размещаться ближе к основанию
сооружения, чтобы уменьшить влияние температурных деформаций и крена.
На гражданских и промышленных зданиях
устанавливают знаки на внутренних и наружных частях сооружения по периметру
через 15 - 20 м, обязательно по углам и по обе стороны осадочных швов.
7.27. Метод створных наблюдений для сдвигов фундаментов
зданий и сооружений применяют там, где можно установить наблюдаемые точки в
один створ и расположить их примерно на одном уровне. На рис. 82 и 83 показаны
схемы расположения пунктов при створном методе наблюдений. В натуре
устанавливают визирный створ, закрепленный на концах неподвижными опорными
знаками.
Длина линии визирования не
должна превышать 500 м. При большей длине линии визирования створ разбивается
на полустворы и четверть створы. Величина сдвига ∆ определяется как
разность отклонений марки от линии створа в двух циклах измерений
где
q1 - отклонение от створа в первом цикле измерений;
q2 - отклонение от створа во втором цикле измерений.
7.28. Створные наблюдения выполняют способом измерения
параллактических углов или с использованием подвижной визирной цели.
7.29. При применении способа параллактических углов (см.
рис. 82) оптический теодолит или алиниометр с окулярным микрометром
устанавливают в наблюдательном пункте I, а неподвижная визирная цель - в пункте II. Затем
несколькими приемами (порядка 4-12 в зависимости от требуемой точности)
измеряют угловое отклонение от створа I-II каждой из наблюдаемых марок.
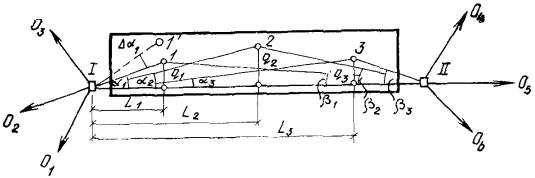
Рис.
82. Метод створа для измерения сдвигов способом параллактических углов
I, II - опорные знаки; О1-O2 - ориентирные знаки; 1-3 - наблюдаемые точки
При этом допускается расхождение между
величинами одного к того же угла, полученными путем полуприемов, не более
3", а расхождение между величинами одного и того же угла, найденными из
разных приемов в прямом и обратном ходе, не более 1,5".
По найденным угловым отклонениям α определяют величину линейного
смещения q относительно створа по формуле
|
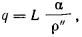
|
(345)
|
где
L -
расстояние от опорного знака до марки, мм;
α - измеренный малый угол, с;
ρ" - 206 265.
7.30. Линейная величина смещения q измеряется непосредственно створным способом с
использованием подвижной визирной цели (см. рис. 83). При измерениях на
конечном опорном знаке I устанавливается теодолит, трубу которого наводят на
неподвижную визирную цель на противоположном опорном знаке II.

Рис.
83. Метод створа для измерения сдвигов с использованием подвижной визирной
цели (см. условные обозначения к рис. 82)
После этого поочередно устанавливают в
каждой из наблюдаемых марок подвижную визирную цель, нивелируют ее и по сигналу
наблюдателя микрометренным винтом передвигают до полного совмещения
вертикальной оси цепи со створами I и II. Положение каждой марки отсчитывают по шкале
микрометренного винта. Затем визирная цель смещается, вновь вводится в створ,
делается новый отсчет и т. д.
Отсчеты и вычисления средних величин
отсчетов для всех марок, начиная с дальней, следует производить не менее 2-5
раз при одном круге инструмента, например при КЛ (первый полуприем). При втором
положении зрительной трубы (при КП измерения ведутся в той же
последовательности, начиная с марки, ближайшей к инструменту (второй
полуприем). Далее вычисляется средний отсчет из полуприемов рср.
После выполнения необходимого числа
приемов (5 - 10), выбираемого в зависимости от удаленности наблюдаемых марок на
одном опорном знаке створа, инструмент переставляют на другой опорный знак, и
наблюдения повторяются.
Расхождение между полуприемами ие должно
превышать 1 мм, а между отдельными приемами - 0,5 мм. Отклонение марки от
створа определяют: при визировании с правого опорного пункта (прямой ход) qn по формуле (346), а при визировании с левого опорного
пункта (обратный ход) q0 по формуле (347).
где
рср -
среднее арифметическое из полуприемов;
МО - место нуля подвижной марки.
Среднее значение отклонения следует
вычислять из n приемов следующим образом:
в прямом ходе
|

|
(348)
|
в обратном ходе
|

|
(349)
|
среднее значение отклонения
|

|
(350)
|
где
Lпр - расстояние от инструмента до марки в прямом ходе;
Lобр - расстояние от инструмента до марки в обратном ходе.
7.31. Метод триангуляции для определения сдвигов фундаментов
применяют при невозможности закрепления створа, когда сооружения расположены в
гористой или пересеченной местности и на слабых основаниях.
Этот метод заключается в построении
специальной сети триангуляции (рис. 84), состоящей из опорных знаков и марок.

Рис. 84. Метод триангуляции для измерения
сдвигов сооружений
А, В, С -знаки триангуляции
В триангуляционной сети измеряют базисы и
углы в треугольниках. В каждом цикле наблюдений производят уравновешивание всей
сети и вычисляют координаты наблюдаемых точек. По разностям координат между
циклами определяют плановое смещение сооружения.
При измерении сдвигов методом
триангуляции допускается условная система координат. В этом случае надо
стремиться к тому, чтобы оси координат х и у совпадали
с поперечной и продольной осями сооружения.
7.32. Наиболее простым методом для измерения сдвигов зданий
и сооружений считают метод направлений.
В этом методе (рис. 85, а) особое внимание уделяют
выбору опорных знаков и обеспечению их неподвижности, которая контролируется в
каждом цикле следующими способами: обратной засечки, триангуляцией, метолом
направлений и т.д. Величину сдвига марок определяют с опорных знаков, не
изменивших своего положения за период между циклами.
Опорные пункты выбираются так, чтобы с
них были видны все марки, а углы засечек с двух пунктов (I, II) были бы
близки к 90°, Нужно стремиться к тому, чтобы направление с одного из опорных знаков
(III) было бы перпендикулярно направлению ожидаемого сдвига q. Расстояние от опорных знаков до марок не должно
превышать 1000 м.
Величины сдвигов марок q, мм, с каждого опорного знака определяют по формуле
|

|
(351)
|
где
L - расстояние от опорного знака до марки, мм (измеряют
с точностью 1:500);
∆α - изменение направления на марку между циклами, с;
ρ" = 206265.
Общую величину и направление сдвига q каждой марки определяют расчетно-графическим способом
(рис. 85, б). Расположение
наблюдаемых и опорных знаков наносят на план строительства и проводят
направления на марки с опорных знаков (I, II). Перпендикулярно каждому направлению в произвольном
масштабе откладывают частные вектора сдвига q1 и q2, определенные
по формуле (351). Окончательную полную величину и направление вектора сдвига
определяют как сумму векторов по правилу перпендикуляров.
В случае устойчивости опорного знака (III), направление которого перпендикулярно направлению
ожидаемого сдвига, величина полного сдвига q может быть определена по формуле (351) с одного
опорного знака (рис. 85, в). Два
других знака (I, II) служат для контроля.
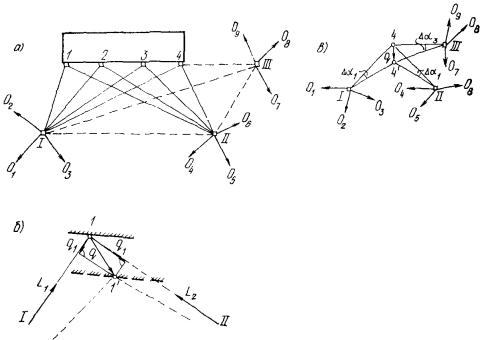
Рис. 85. Метод
направлений для измерения сдвигов
а - схема расположения знаков; б
- расчетно-графический способ определения сдвига; в - принцип получения сдвига при одном створном знаке (см. условные
обозначения к рис. 82)
7.33. Комбинированный метод измерения сдвигов сооружений
(рис. 86) применяют в случае неустойчивых опорных знаков. При этом наблюдения
за взаимными смещениями точек осуществляют любым створным способом, а
устойчивость опорных пунктов проверяют методом триангуляции или направлений.

Рис. 86. Комбинированный метод измерения
сдвигов
А, В, С, Д, Е, F - знаки триангуляции
7.34. Измерение кренов зданий и сооружений выполняют
вертикальным проектированием посредством измерения горизонтальных углов и по
результатам измерений осадок фундамента.
7.35. При определении крена вертикальным проектированием
(рис. 87, а) выбирают заметную точку
в верхней части здания и проектируют ее теодолитом вниз на цокольную часть
здания или специально закрепленную в цоколе линейку. Расстояние между
проекциями этой точки, полученное по двум циклам проектирования, отнесенное к
высоте здания или сооружения, определяет величину крена.
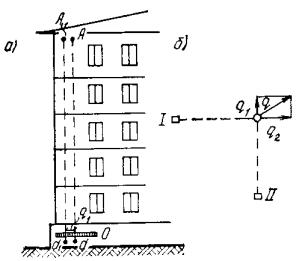
Рис. 87. Определение крена вертикальным
проектированием
а - схема проектирования наблюдаемой
точки на цоколь здания; б -
графическое определение общего крена здания
Для получения полной величины крена угла
здания измеряют проекции выбранной точки здания с двух взаимно перпендикулярных
сторон (рис. 87, б), определяют
частные вектора r1 с опорного знака I и r2 со стороны
знака II, а затем по правилу параллелограмма получают величину
полного линейного крена сооружения (проекции точки)
Полный относительный крен i сооружения определяется по формуле
|

|
(353)
|
где
r - величина полного линейного крена сооружения;
Н -
высота сооружения.
7.36. При определении крена координатным способом около
сооружения устанавливают 2-3 опорных знака, устойчивость которых проверяют в
каждом цикле наблюдений методом триангуляции или направлений. Из опорных точек
периодически прямой засечкой определяют координаты верхних и нижних точек
сооружения. По разностям координат находят величину крена в течение
определенного промежутка времени, а также его направление.
Относительный крен вычисляют по формуле
(353).
7.37. Наиболее надежным способом наблюдений за креном
сооружения считают периодическое измерение горизонтальных углов, между
неизменными направлениями (IO1, IIO2) и направлениями (IA, IIА) на верхнюю наблюдаемую точку А с помощью точного теодолита,
установленного в опорных точках I и II (рис. 88).
По величине изменения горизонтальных
углов с течением времени ∆α1
и ∆α2 и
горизонтальному расстоянию до наблюдаемой точки по формулам (346) находят составляющие крена r1, r2 и полную линейную величину крена r:
|
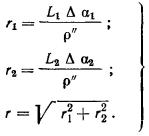
|
(354)
|
Также определяют приращение крена точки В, расположенной внизу этой же
наружной грани стены. Разница приращений кренов точек А и В, отнесенная к высоте AВ показывает полную величину крена
сооружения.

Рис. 88. Измерение крена методом
горизонтальных углов
7.38. Для определения кренов применяют высокоточное
геометрическое нивелирование относительно исходного репера стенных марок,
установленных с четырех противоположных сторон сооружения (рис. 89). По
разностям осадок в двух взаимно перпендикулярных направлениях по правилу
параллелограмма определяют величину фундамента наклона ∆S. Зная расстояние l между марками и высоту Н сооружения, можно вычислить величину
крена i сооружения

Рис.
89. Определение крена методом нивелирования
7.39. Крен дымовых труб или других сооружений башенного
типа, имеющих форму усеченного конуса, определяют методом вертикального
проектирования либо посредством измерений горизонтальных углов.
7.40. При способе вертикального проектирования (рис. 90, а) визирную ось теодолита,
установленного на опорном пункте I, по очереди наводят на боковые грани сооружений
(точки 1 и 2) и проектируют их по двум
положениям трубы на верхнюю часть фундамента (точки 1' и 2'). Проекция
центра верха трубы (точка а')
находится на середине расстояния между точками 1 и 2.
Повторяя то же самое через некоторый
промежуток времени, находят новое положение проекции центра верха трубы а". Отрезок а' а" показывает величину
крена r1 в соответствующем направлении.
Также вычисляют составляющую крена r2 с опорного пункта II, расположенного на направлении, перпендикулярном
первому. Полное приращение крена определяют по формуле (352).
7.41. Для определения крена трубы посредством измерений
горизонтальных углов (рис. 90, б) на
образующей трубы намечают постоянные точки наблюдений 1, 2, 3 и 4. На
расстоянии L1 от трубы
с опорного знака I измеряют горизонтальные углы на точки 1, 2, 3 и 4. Вычисляют полуразности углов  , которые определяют направления на центр верха трубы А и центр низа трубы В. По формуле (355) вычисляют величину поперечного крена rр в данном направлении. , которые определяют направления на центр верха трубы А и центр низа трубы В. По формуле (355) вычисляют величину поперечного крена rр в данном направлении.
С опорного пункта II измеряют
направление на точки 5, 6, 7, 8 и по
результатам этих измерений вычисляют составляющую крена r2 в этом направлении и полную линейную величину крена сооружения r.
Измерения повторяют через определенные
интервалы времени.
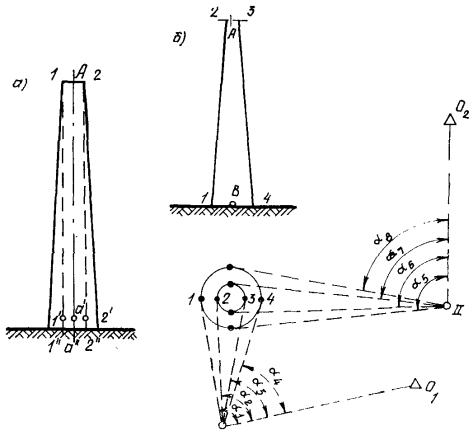
Рис. 90. Определение крена дымовых труб
а -
способом вертикального проектирования; б - способом измерения горизонтальных углов
7.42.
После проведения необходимого
количества циклов измерений осадок, сдвигов и кренов сооружения составляют пояснительную записку или
научно-технический отчет, где анализируются результаты наблюдений за изменением
осадок, сдвигов и кренов различных зданий и сооружений.
В отчетных документах проводят схемы
расположения наблюдаемых марок, опорных контрольных и ориентирных знаков; дают
графики и эпюры осадок, сдвигов или кренов в зависимости от времени и величины
вертикальной или горизонтальной нагрузки; описывают инженерно-геологическое
строение основания и физико-механические свойства грунтов; излагают конструктивные
особенности сооружения и фундамента.
В заключение приводят выводы о степени
надежности и устойчивости зданий и сооружений, делают прогнозы дальнейших
приращений осадок, сдвигов и кренов, в случае необходимости рекомендуют
мероприятия по предупреждению недопустимых осадок, сдвигов и кренов для данного
вида сооружения, уточняют дальнейшую методику проведения работ.
ПРИЛОЖЕНИЕ
1
|
Шифр программы
|
Характеристики программ
|
|
тип ЭВМ
|
язык программы
|
разработчики программы
|
расчетная схема
|
форма фундамента в плане
|
расчетная категории фундамента
|
метод расчета фумента
|
учет касательных напряжений по подошве
фундамента
|
Учет касательных напряжений между фундаментом
и надфундаментными конструкциями
|
учет односторонних связей между фундаментом
и основанием
|
|
основной
|
возможный
|
основания
|
фундамента
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
|
РПС-3
|
Минск-22
|
Минск-32 (в режиме совместимости)
|
АКИТ
|
Челябинский политехнический институт
|
Основание, подчиняющееся гипотезе
переменного или постоянного коэффициента жесткости
|
Континуальная
|
Прямоугольная
|
Тонкий
|
Конечно-разностный
|
Не производится
|
Не производится
|
Не производится
|
|
МРП-3
|
М-220М
|
М-222
|
АЛГОЛ-60
|
НИИОСП
|
Линейно-деформируемое полупространство с
корректирующим коэффициентом при модуле деформации основания
|
Континуальная
|
Прямоугольная
|
Тонкий
|
Двойных полиномов, интегралов Фурье-Бесселя
|
Не производится
|
Не производится
|
Не производится
|
|
ПУО-5
|
М-220М
|
БЭСМ-3 БЭСМ-4
|
Коды ЭВМ
|
Ленпромстройпроект
|
Основание, подчиняющееся гипотезе двух
коэффициентов постели или постоянного коэффициента жесткости
|
Континуальная
|
Прямоугольная
|
Тонкий
|
Конечно-разностный
|
Не производится
|
Не производится
|
Не производится
|
|
СУПЕР-76
|
Минск-32
|
|
ФОРТРАН
|
Гипро-
химмаш
|
Основание, подчиняющееся гипотезе двух коэффициентов
постели, постоянного или переменного коэффициента жесткости
|
Континуальная
|
Произвольная
полигонального
|
Тонкий
|
Конечного элемента
|
Не производится
|
Производится
|
Не производится
|
|
ЦНИИСК-100
|
М-222
|
М-220
Минск-32
|
АЛГОЛ-60
|
ЦНИИСК
|
Основание, подчиняющееся гипотезе
переменного коэффициента жесткости
|
Дискретная
|
Произвольная
|
Тонкий
|
Перемещение с использованием для усилий
конечно-разностных соотношений
|
Не производится
|
Производится
|
Производится
|
|
ЦНИИСК-101
|
М-222
|
Минск-32
|
АЛГОЛ-60
|
ЦНИИСК Госстроя СССР
|
Основание, подчиняющееся гипотезе переменного
коэффициента жесткости
|
Дискретная
|
Произвольная
|
Тонкий
|
Перемещение с использованием для усилий конечно-разностных соотношений
|
Не производится
|
Производится
|
Производится
|
|
ППП
АПЖБК
|
ЕС ЭВМ с разделом оперативной памяти пользователя
не менее 120к
|
|
PL/I
и Ассемблер Различные версии ОС; РСР; 4; 4,1
|
НИИАСС Госстроя УССР
|
Основание, подчиняющееся гипотезе двух коэффициентов
постели и переменного коэффициента жесткости
|
Континуальная
|
Произвольная полигональная
|
Тонкий, средней толщины и толстый
|
Конечного элемента
|
Не производится
|
Производится
|
Не производится
|
|
ПЛИСКА (плита с каркасом)
|
Минск-32
|
|
ФОРТРАН-IV
|
Моспроект-1
|
Основание, подчиня-
ющееся
гипотезе
двух
коэффи-
циентов
постели и перемен-
ного
коэффи-
циента жесткости
|
Конти-
нуальная
|
Произ-
вольная
полиго-
нальная
|
Тонкий
|
Конечного элемента
|
Не произ-
водится
|
Произ-
водится
|
Не произ-
водится
|
|
РАФУП-3
|
БЭСМ-6
|
|
ФОРТPAH-IV
|
НИИСК
|
Основание, подчиня-
ющееся
гипотезе перемен-
ного
коэффи-
циента жесткости
|
Конти-
нуальная
|
Прямо-
угольная
|
Тонкий
|
Конечно-
разностный
|
Не произ-
водится
|
Не
произ-
водится
|
Не произ-
водится
|
|
ПРОЛОГ-4
|
ЕС-1030
|
Минск-32
|
ФОРТРАН-IV
|
НИИСК
|
Основание, подчиня-
ющееся
гипотезе перемен-
ного
коэффи-
циента жесткости
|
Не исполь-
зуется
|
Прямо-
угольная
|
Не исполь-
зуется
|
Не
исполь-
зуется
|
Не произ-
водится
|
Не
произ-
водится
|
Не произ-
водится
|
|
АРПОС-2
|
ЕС ЭВМ с объемом внутренней
памяти не менее 128 к
|
|
ФОРТPAH-IV ДОС
|
Челябин-
ский политех-
нический институт
|
Линейно-дефор-
мируемый слой;
основание, подчиня-
ющееся гипотезе постоянного или переменного коэффи-
циента
жесткости; комбинация этих моделей
|
Конти-
нуальная
|
Круглая или кольце-
вая
|
Тонкий
|
Вариа-
ционно-
разнос-
тный
|
Не произ-
водится
|
Не
произ-
водится
|
Не произ-
водится
|
|
ПОРТИК
|
Минск-22 Минск-32
|
|
АКИТ
|
Челябин-
ский политех-
нический институт
|
Основание, подчиня-
ющееся гипотезе
перемен-
ного коэффи-
циента жесткости
|
Конти-
нуальная
|
Произ-
вольная ортого-
нальная
|
Тонкий
|
Вариа-
ционно-
разнос-
тный
|
Не произ-
водится
|
Не
произ-
водится
|
Не произ-
водится
|
|
НРП-2
|
ЕС ЭВМ
|
|
ФОРТPAH-IV
|
Челябин-
ский политех-
нический институт
|
Основание, подчиня-
ющееся гипотезе
перемен-
ного коэффи-
циента жесткости
|
Конти-
нуальная
|
Произ-
вольная ортого-
нальная
|
Тонкий
|
Вариа-
ционно-
разнос-
тный
|
Не произ-
водится
|
Не
произ-
водится
|
Не произ-
водится
|
|
ПРОФКОН
|
ЕС-1022 с256 к и двумя диско-
водами
|
Более мощные модели ЕС ЭВМ
|
ФОРТРАН-IV PL/1
|
Харьков-
ский
пром-
стройнии-
проект
|
Упругое
однород-
ное и неодно-
родное полу-
простран-
ство;
упругий
слой конечной толщины,
модель
Вииклера;
модель с переменным коэффи-
циентом жесткости; комбини-
рованные 2-слойные
модели
|
Диск-
ретная
|
Произ-
вольная
|
Тонкий
|
Переме-
щений
с использо-
ванием
для
усилий конечно- разнос-
тных соотно-
шений
|
Не произ-
водится
|
Произво-
дится
|
Не произ-
водится
|
|
КОРПУС-ЕС
|
ЕС ЭВМ с объемом основной памяти раздела
пользо-
вателя не менее
166 К
|
|
PL/1
ОС 4.0
|
Ленпром-
строй-
проект
|
Основание с двумя коэффи-
циентами же-
сткости и перемен-
ным коэффи-
циентом жесткости
|
Конти-
нуальная
|
Произ-
вольная полиго-
нальная
|
Тонкие и средней толщины
|
Конечных элементов
|
Не произ-
водится
|
Не
произ-
водится
|
Не произ-
водится
|
|
КОЛЬЦО
|
М-222
|
М-20 БЭСМ-6
|
АЛГОЛ ТА-IМ
|
Уральский промстрой
ниипроект н уральский политех-
нический институт
|
Основание, подчиняющееся гипотезе
постоянного коэффициента постели
|
Конти-
нуальная
|
Кольцева
|
Тонкий
|
Конечно-
разностный
|
Не произ-
водится
|
Не
произ-
водится
|
Не произ-
водится
|
|
ТИТАН
|
М-222
|
М-20 БЭСМ-6
|
АЛГОЛ TA-IM
|
Уральский промстрой-
ннипроект
и политех-
ничес кий
институт
|
Основание, подчиня-
ющееся
гипотезе постоянного коэффи-
циента
постели
|
Конти-
нуальная
|
Кольцева
|
Тонкий
|
Конечно-
разностный
|
Не произ-
водится
|
Не
произ-
водится
|
Не произ-
водится
|
|
ЯНУС
|
М-222
|
М-20 БЭСМ-6
|
АЛГОЛ TA-IM
|
Уральский промстрой-
ннипроект
и политех-
ничес кий
институт
|
Основание, подчиня-
ющееся
гипотезе постоянного коэффи-
циента
постели
|
Конти-
нуальная
|
Кольцева
|
Тонкий
|
Конечно-
разностный
|
Не произ-
водится
|
Не
произ-
водится
|
Не произ-
водится
|
|
МИМАС
|
М-222
|
М-20 БЭСМ-6
|
АЛГОЛ TA-IM
|
Уральский промстрой-
ннипроект
и политех-
нический
институт
|
Основание, подчиня-
ющееся
гипотезе постоянного коэффи-
циента
постели
|
Конти-
нуальная
|
Кольцевая
|
Тонкий
|
Конечно-
разностный
|
Не произ-
водится
|
Не
произ-
водится
|
Не произ-
водится
|
|
Сведкоши
|
М-222
|
М-20 БЭСМ-6
|
АЛГОЛ ТА-IМ
|
Уральский ПСП и Уральскнй политех-
нический
|
Основание, подчиня-
ющееся
гипотезе постоянного коэффи-
циента
постели
|
Конти-
нуальная
|
Кольцевая
|
Тонкий
|
Конечно-
разностный
|
Не произ-
водится
|
Не произ-
водится
|
Не произ-
водится
|
|
ФКО-1
|
М-222
|
М-220М
|
АЛГОЛ-60
|
ГрузНИИ-ЭГС
|
Линейно-
деформи-
руемое
полупро-
странство с коррек-
тирующим коэффи-
циентом при модуле
дефор-
мации
грунта
|
Конти-
нуальная
|
Полосовая
|
Тонкий
|
Наложение фиктивных ортотро-
пных систем
|
Произ-
водится
|
Произ-
водится
|
Не произ-
водится
|
|
ФКО-2
|
М-222
|
М-220М
|
АЛГОЛ-60
|
ГрузНИИ-ЭГС
|
Линейно-
деформи-
руемое
полупро-
странство с коррек-
тирующим коэффи-
циентом при модуле
дефор-
мации
грунта
|
Конти-
нуальная
|
Полосовая
|
Тонкий
|
Наложение фиктивных ортотро-
пных систем
|
Произ-
водится
|
Произ-
водится
|
Не произ-
водится
|
|
ТФП
|
М-222
|
М-220М
|
АЛГОЛ-60
|
ГрузНИИ-ЭГС
|
Линейно-
деформи-
руемое
полупро-
странство с коррек-
тирующим коэффи-
циентом при модуле
дефор-
мации
грунта
|
Конти-
нуальная
|
Полосовая
|
Толстый
|
Наложение фиктивных ортотро-
пных систем
|
Произ-
водится
|
Произ-
водится
|
Не произ-
водится
|
|
РКП-2
|
ЕС
|
ОДРА-1204
|
ФОРТРАН АЛГОЛ
|
НИИ меха-
ники и прикладной математики Ростов-
ского государ-
ственного универ-
ситета
|
Линейно-
деформи-
руемое
основание с произвольно изменя-
ющимися по глубине характе-
ристиками
|
Конти-
нуальная
|
Круглая
|
Тонкий и средней толщины
|
Ортонор-
миро-
ванных
поли-
номов
|
Не произ-
водится
|
Не произ-
водится
|
Не произ-
водится
|
|
ПЛУТОН
|
ЕС-1022
|
ЕС
|
ФОРТРАН
|
ЦНИИ Промзер-нопроект
|
Линейно-
дефор-
мируемое полупрос-
транство,
слой;
осно-
вание
с постоян-
ным,
перемен-
ным коэффици-
ентами
жесткости, комбини-
рованное
|
Конти-
нуальная
|
Прямо-
угольная
|
Тонкий
|
Конечных разностей в сочетании с методом
Б.Н. Жемочкииа
|
Не произ-
водится
|
Не
произ-
водится
|
Не произ-
водится
|
|
ПРОСТОР
|
ЕС-1022
|
ЕС
|
ФОРТРАН
|
ЦНИИ Промзер-нопроект
|
Линейно-
дефор-
мируемое полупро-
странство, комбини-
рованное
|
Конти-
нуальная
|
Полосовая
|
Тонкий
|
Смешан-
ный метод строитель-
ной меха-
ники в соче-
тании с методом
Б.Н. Жемочкин
|
Произ-
водится
|
Произ-
водится
|
Не произ-
водится
|
|
GEST
|
ЕС ЭВМ
|
ЕС
|
ФОРТPAH-IV
|
НИИОСП
ГСПИ
|
Линейно-деформи-
руемое
полупро-
странство,
условно
ограни-
ченное
по глубине,
слой,
пере-
менный
коэффи-
циент
жесткости
|
Не исполь-
зуется
|
Прямо-
угольная
|
Не исполь-
зуется
|
Не исполь-
зуется
|
Не произ-
водится
|
Не произ-
водится
|
Не произ-
водится
|
|
РАПОРТ
|
М-220 ЕС ЭВМ
|
ЕС
|
АЛГОЛ-60 ФОРТPAH-IV
|
НИИОСП
ГСПИ
|
Линейно-
дефор-
мируемое полупро-
странство с корректи-
рующим
коэффи-
циентом
при модуле деформации основания
|
Конти-
нуальная
|
Прямо-
угольная
|
Тонкий
|
Двой-
ных
поли-
номов,
инте-
гралов Фурье-
Бесселя
|
Не произ-
водится
|
Не произ-
водится
|
Не произ-
водится
|
|
ЖОК
|
М-222 ЕС ЭВМ
|
ЕС
|
АЛГОЛ-60 ФОРТРАН-IV
|
НИИОСП
ГСПИ
|
Основание подчиня-
ющееся
гипотезе
перемен-
ного
коэффи-
циента
жесткости
|
Конти-
нуальная
|
Прямо-
угольная
|
|
Двой-
ных
поли-
номов,
инте-
гралов Фурье-
Бесселя
|
Не произ-
водится
|
Не произ-
водится
|
Не произ-
водится
|
|
ПРЕДЕЛ
|
М-222
|
ЕС
|
АЛГОЛ-60
|
Уральский Промстрой-ниипроект
|
Неде-
форми-
руемое
|
Конти-
нуальная
|
Круглая
|
Тонкий
|
Симплек
|
Не произ-
водится
|
Не произ-
водится
|
Не произ-
водится
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продолжение приложения 1
|
Шифр программы
|
Характеристики програмы
|
|
учет переменной толщины фундамента
|
учет неодно-
родности основания в плане
|
учет жесткости верхнего строения
|
учет
особен-
ностей
дефор-
мирования железо-
бетона
|
оптими-
зация расчета
|
сокра-
щенная запись исходных данных в табличном виде
|
дополни-
тельные блок
|
Программы используются при
|
|
числе
|
выполнение прочих ограничений
|
|
загру-
жений за один расчет
|
нагрузок в одном зaгружении
|
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
|
РПС-3
|
Произво-
дится
|
Учиты-
вается
|
Учиты-
вается
|
Не учиты-
вается
|
Отсутс-
твует
|
Есть
|
Отсутс-
твуют
|
5
|
Без ограни-
чений
|
Число узлов разностной сетки до 2000
|
|
МРП-3
|
Не произво-
дится
|
Не учиты-
вается
|
Учитывается
|
Не учиты-
вается
|
Отсутс-
твует
|
Отсутс-
твует
|
Отсутс-
твует
|
1
|
120
|
Отсутс-
твуют
|
|
ПУО-5
|
Не произво-
дится
|
Не учитывается
|
Не учиты-
вается
|
Не учиты-
вается
|
Отсутс-
твует
|
Есть
|
Отсутс-
твуют
|
|
Без ограни-
чений
|
Отсутс-
твуют
|
|
СУПЕР-76
|
Произво-
дится
|
Учиты-
вается
|
Учиты-
вается
|
Не учиты-
ваетс
|
Отсутс-
твует
|
Есть
|
Отсутс-
твует
|
30
|
Без ограни-
чений
|
Число неизвес-
тных не более 3500
|
|
ЦНИИСК-
100
|
Произво-
дится
|
Учиты-
вается
|
Не учиты-
вается
|
Не учиты-
вается
|
Отсутс-
твует
|
Отсутс-
твует
|
Отсутс-
твует
|
1
|
1000
|
Число узлов
до 500
|
|
ЦНИИСК-
101
|
Произво-
дится
|
Учиты-
вается
|
Учиты-
вается
|
Не учиты-
вается
|
Отсутс-
твует
|
Отсутс-
твует
|
Отсутс-
твует
|
1
|
1000
|
Число
разно-
типных линейных элементов
до 100
|
|
ППП
АПЖБК
|
Произво-
дится
|
Учиты-
вается
|
Учиты-
вается
|
В статике
не учиты-
вается в армиро-
вании учиты-
вается
|
Не произво-
дится
|
Есть
|
Армиро-
вание фунда-
мента
|
Не более 100
|
Без ограни-
чений
|
Ограни-
чением является
время
счета,
число
узлов
до 3200
|
|
ПЛИСКА (плита с каркасом)
|
Произво-
дится
|
Учиты-
вается
|
Учиты-
вается
|
В ста-
тике не
учиты-
вается. В армиро-
вании
учиты-
вается
|
Не произ-
водится
|
Есть
|
Графический
вывод
информации,
автоматическое
формирование
расчетной
модели
с выводом
на листинг,
логический
и визуальный
контроль.
Задание
информации
на уровне
описания
чертежа
|
5
|
Без ограни-
чений
|
Суммарное
число
неизвестных пространс-
твенной
модели,
включая
диски
перекрытий,
стены,
плиты
до 3500
|
|
РАФУП-3
|
Не произ-
водится
|
Учиты-
вается
|
Не учиты-
вается
|
Не учиты-
вается
|
Не произво-
дится
|
Отсутс-
твует
|
Отсутс-
твует
|
Без ограни-
чений
|
Без ограни-
чений
|
Отсутс-
твуют
|
|
ПРОЛОГ-4
|
Не произ-
водится
|
Учиты-
вается
|
Не учиты-
вается
|
Не учиты-
вается
|
Не произво-
дится
|
Есть
|
Отсутс-
твует
|
Без ограни-
чений
|
Без ограни-
чений
|
Отсутс-
твуют
|
|
АРПОС-2
|
Произво-
дится
|
Учиты-
вает-
ся по радиусу
|
Учиты-
вается
|
Учиты-
вается
|
Произво-
дится опти-
мальное армиро-
вание
|
Есть
|
Отсутс-
твует
|
1
|
30
|
Число узлов сетки по радиусу до 32
|
|
ПОРТИК
|
Произво-
дится
|
Учиты-
вается
|
Учиты-
вается
|
Не учиты-
вается
|
Не произ-
водится
|
Есть
|
Отсутс-
твуют
|
До 200
|
До 200
|
Число узлов сетки до 3000
|
|
НРП-2
|
Произво-
дится
|
Учиты-
вается
|
Не учиты-
вается
|
Учиты-
вается
|
Не произ-
водится
|
Есть
|
Отсутс-
твуют
|
1
|
Без ограни-
чений
|
Число
узлов сетки
до 2000
|
|
ПРОФКОН
|
Произво-
дится
|
Учиты-
вается
|
Учиты-
вается
|
Не учиты-
вается
|
Не произ-
водится
|
Есть
|
Логи-
ческий
контроль
инфор-
мации
|
Формально ограничены
не числом, а размером
массивов, отведенных
для загружения
|
Количество стержней
и узлов и дискретной
схемы до 29999;
расши-
ренная
матрица
системы
уравнений
должна
целиком
разме-
щаться
на 1 томе
внешнего
запоми-
нающего
устройства
|
|
КОРПУС-ЕС
|
|
Учиты-
вается
|
Учиты-
вается в предполо-
жении
абсолютно жесткого верхнего строения и упруго-
деформи-
руемых
стоек
|
Не учиты-
вается
|
Не произ-
водится
|
Есть
|
Блоки выбора наихудшей комбинации
(разработка) Харьковского промстрой-
ннипроекта)
|
Без ограничений
|
Число узлов
сетки до 2000
|
|
КОЛЬЦО
|
Произво-
дится
|
Не учиты-
вается
|
Не учиты-
вается
|
Не учиты-
ваетс
|
Не произ-
водится
|
Отсутс-
твует
|
Отсутс-
твую
|
1
|
Без ограни-
чений
|
Отсутс-
твуют
|
|
ТИТАН
|
Произво-
дится
|
Не учиты-
вается
|
Не учиты-
вается
|
Не учиты-
ваетс
|
Не произ-
водится
|
Отсутс-
твует
|
Отсутс-
твую
|
1
|
Без ограни-
чений
|
Отсутс-
твуют
|
|
ЯНУС
|
Произво-
дится
|
Не учиты-
вается
|
Не учиты-
вается
|
Не учиты-
ваетс
|
Не произ-
водится
|
Отсутс-
твует
|
Отсутс-
твую
|
1
|
Без ограни-
чений
|
Отсутс-
твуют
|
|
МИМАС
|
Произво-
дится
|
Не учиты-
вается
|
Не учиты-
вается
|
Не учиты-
ваетс
|
Не произ-
водится
|
Отсутс-
твует
|
Отсутс-
твую
|
1
|
Без ограни-
чений
|
Отсутс-
твуют
|
|
Сведкоши
|
Произво-
дится
|
Не учиты-
вается
|
Не учиты-
вается
|
Не учиты-
ваетс
|
Не произ-
водится
|
Отсутс-
твует
|
Отсутс-
твую
|
Без ограни-
чений
|
Отсутс-
твуют
|
|
ФКО-1
|
Не произ-
водится
|
Не учиты-
вается
|
Учиты-
вается
|
Не учиты-
ваетс
|
Не произ-
водится
|
Отсутс-
твует
|
Отсутс-
твую
|
Без ограни-
чений
|
Отсутс-
твуют
|
|
ФКО-2
|
Не произ-
водится
|
Не учиты-
вается
|
Учиты-
вается
|
Не учиты-
ваетс
|
Не произ-
водится
|
Отсутс-
твует
|
Отсутс-
твуют
|
Без ограни-
чений
|
Отсутс-
твуют
|
|
ТФП
|
Не произ-
водится
|
Не учиты-
вается
|
Не учиты-
вается
|
Не учиты-
ваетс
|
Не произ-
водится
|
Не произ-
водится
|
Отсутс-
твуют
|
Без ограни-
чений
|
Отсутс-
твуют
|
|
ПРЕДЕЛ
|
Не произ-
водится
|
Не учиты-
вается
|
Не учиты-
вается
|
Учиты-
вается
|
Произ-
водится
|
Произ-
водится
|
Отсутс-
твуют
|
Без ограни-
чений
|
Отсутс-
твуют
|
|
РКП-2
|
Не произ-
водится
|
Не учиты-
вается
|
Не учиты-
вается
|
Не учиты-
ваетс
|
Не произ-
водится
|
Отсутс-
твует
|
Отсутс-
твуют
|
Без ограни-
чений
|
Показатель гибко-
сти до 50
|
|
ПЛУТОН
|
Не произ-
водится
|
Учиты-
вается
|
Учиты-
вается
|
Не учиты-
ваетс
|
Не произ-
водится
|
Отсутс-
твует
|
Отсутс-
твуют
|
1
|
Без ограни-
чений
|
Число узлов сетки до 121
|
|
ПРОСТОР
|
Произ-
водится
|
Не учиты-
вается
|
Учиты-
вается
|
Не учиты-
ваетс
|
Не произ-
водится
|
Отсутс-
твует
|
Отсутс-
твуют
|
1
|
Без ограни-
чений
|
Число
неизвес-
тных
не более 200 Число верти-
кальных или горизон-
тальных
участков не более 20
|
|
GEST
|
Не произ-
водится
|
Учиты-
вается
|
Не учиты-
вается
|
Не учиты-
вается
|
Произ-
водится
|
Отсутс-
твует
|
Отсутс-
твуют
|
1
|
Без ограни-
чений
|
Отсутс-
твуют
|
|
РАПОРТ
|
Не произ-
водится
|
Не учиты-
вается
|
Не учиты-
вается
|
Не учиты-
вается
|
Произ-
водится
|
Отсутс-
твует
|
Отсутс-
твуют
|
1
|
120
|
Отсутс-
твуют
|
|
ЖОК
|
Не произ-
водится
|
Учиты-
вается
|
Не учиты-
вается
|
Не учиты-
вается
|
Не произ-
водится
|
Отсутс-
твует
|
Отсутс-
твуют
|
1
|
120
|
Отсутс-
твуют
|
|
|
|
|
|
|
|
|
|
|
|
|
ПРИЛОЖЕНИЕ
2
Осадки и крены определяются как для абсолютно
жестких фундаментов по формулам:
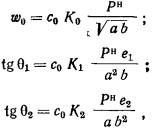
где w0 - осадка центра фундамента;
θ1 - угол
поворота продольной оси фундамента;
θ2 - угол
поворота поперечной оси фундамента;
а -
полудлина подошвы фундамента;
b - полуширина подошвы фундамента;
Рн -
суммарное вертикальное усилие от нормативной нагрузки, приложенной к
фундаменту;
е1 -
расстояние точки приложения усилия Рн - от центра фундамента по продольной оси;
е2 -
расстояние точки приложения усилия Рн от центра фундамента по поперечной оси;
Eср μср, И-ср - осредненные в пределах
сжимаемой толщи модуль деформации и коэффициент Пуассона грунта;
K0, К1, К2 - безразмерные коэффициенты, определяемые по приведенным ниже
графикам (рис. 1, 2). Графики построены в зависимости от отношения большей
стороны фундамента к меньшей (величина δ
= a/b) и толщины
слоя h0 к ширине фундамента (величина λ = h0/2b). Вдоль
горизонтальной оси графика К - δ отложена величина δ,
графика К - λ.- величина λ. Вдоль вертикальной оси обоих
графиков отложены безразмерные коэффициенты K0, К1, К2 - Оба
графика независимы.
Графики построены по
результатам расчетов, выполненных иа ЭВМ М-222 по программе ШТАМП-2,
разработанной в институте Харьковский Промстройниипроект,
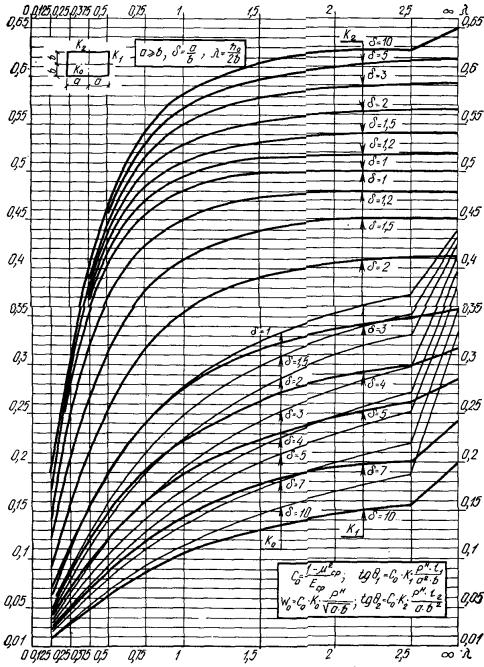
Рис
1. График k
- λ для
определения безрамерных коэффициентов K0, К1, К2 используемых при вычислении осадки и кренов прямоугольного
жесткого фундамента на полупространстве (λ = ∞) и слое толщиной h0
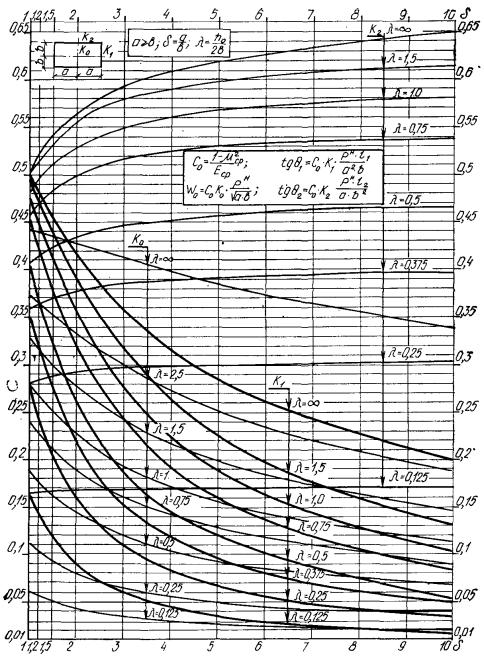
Рис.
2. График k -
δ для определения безразмерных коэффициентов K0, К1, К2, используемых при вычислении осадки и кренов прямоугольного
жесткого фундамента на полупространстве (λ = ∞) и слое толщиной h0
ПРИЛОЖЕНИЕ
3
Осадки и крены определяются как для абсолютно
жестких фундаментов по формулам:

где w0 - осадка центра фундамента;
θ
- угол поворота оси фундамента, вдоль которой определяется крен;
R -
радиус круглого фундамента;
Pн - суммарное вертикальное
усилие от нормативной нагрузки, приложенной к фундаменту;
r -
расстояние от центра фундамента до точки приложения усилия Pн;

График
k
- λ для
определения безразмерных коэффициентов К0 и К1 используемых
для вычисления осадки и крена круглого жесткого фундамента на полупространстве
(λ = ∞) и слое
толщиной h0
φ - угол, образуемый
осью, вдоль которой определяется крен, с радиусом, проходящим через точку
приложения усилия Рн

Еср, и
μср - осредненные в пределах сжимаемой толщи модуль
деформации и коэффициент Пуассона грунта;
К0, К1 -
безразмерные коэффициенты, определяемые по графику (см. рисунок).
Графики построены в
зависимости от величины λ - отношения толщины слоя h0 к диаметру
фундамента 2R. Для фундаментов на полупространстве λ принимается равной ∞.
При λ, превосходящем
2,5, допускается определять коэффициент К0 по формуле
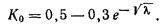
|
|